网络流学习笔记

最大流

类型一路径覆盖

P2764 最小路径覆盖问题

我们考虑初始情况下，每个点都独立作为一条路径存在，当我们合并两条路径时，总路径数减一，若要使总路径数最小，则要使得合并的路径最多。同时，路径之间的合并是不会互相干扰的，那么我们只需要找出一个方案使得配对数最多即可，这个问题等价于二分图最大匹配，直接 Dinic 即可解决。

最后的答案即为总点数 - 最大匹配数。

P2765 魔术球问题

注意到球与球之间存在限制关系，考虑建图，对于两个号码为 $x,y$ 的球建立一条边 $(x,y)$ 当且仅当满足 $ x < y$ 且 $x+y$ 为平方数。建图后一个柱子对应的就是一条路径，不断枚举答案，每次都求出最小路径覆盖，若加入第 $i$ 个球时最小路径数大于柱子数，则答案为 $i-1$。

类型二二分图类问题

P3511 [POI2010] MOS-Bridges

看到最小化最大值首先可以二分，问题转化为在一个图上判定是否有欧拉回路。

但是我们发现这个图同时存在双向边和单向边，不能直接判断，我们可以考虑欧拉回路的判定：

图联通
所有点度数均为偶数且入度与出度相等

第一点默认已经实现，第二点可以看成入度为度数一半，度数显然为定值。

我们考虑一条双向边只有可能为两个端点中的一个增加一个入度，所以我们可以将边与点进行匹配，将边向两个端点连流量为 1 的边，点向汇点连 $\dfrac{degree(i)}{2}$ 的边，源点向边连 $1$ 的边。然后流，最大流若为所有度数和的一般则证明存在欧拉回路。

输出方案 dfs 即可。

类型三普通最大流

P2754 [CTSC1999] 家园 / 星际转移问题

首先通过讨论区可知答案最大为1000。

我们从小到大暴力枚举答案，每次用分层图的方式建图，对于一个时间，若飞船从 $x$ 飞到 $y$，则将 $x_{t-1}$ 向 $y_t$ 连边边权为人数。

跑流，当最大流大于总人数时，说明已经可以全部完成运输。

由于 Dinic 前面跑过的流不用再跑，~~所以复杂度是正确的。~~其实这题复杂度就tm是错的。只不过数据没卡。

最小割

前置知识：最大流最小割定理

最大流=最小割

证明：根据定义，显然割 $\geq$ 最大流。然后我们考虑能否一定构造出一个方案使得两者相等。我们遍历 $dis$ 找出图的连通性对于一条边，若其两个端点在不同的点集之中且流量为 $0$（即流满了）,那么这条边一定为割边，我们发现，所有的这些边的边权其实就是所在流的流量，那么边权和自然就是最大流，则这个割等于最大流，又因为割 $\geq$ 最大流，所以此方案即为最小割。得证。

类型一最大权闭合子图问题

此类问题一般为以下形式：

给定一个有向图，点有点权，选择一个子图，满足子图上如果选择了一个点就必须选择它后继的所有点。最大化点权和。

由于如果一个图内一个点被选择了则后继必须被选择，那么称该图是闭合的，因此该问题称为最大权闭合子图问题。

P2762 太空飞行计划问题

我们考虑先拿满所有的报酬，再减去最小的成本。

我们将实验分为一组点，机器分为另一组，将实验向所需的机器连 inf 边，源点向实验连报酬边，机器向汇点连售价边，然后求最小割（最大流），将图分为两部分，与源点连通的点即为取的点。

注意输出方案不能直接判断与 $s$ 与 $t$ 相连的剩余流量为 $0$ 的点输出，反例：

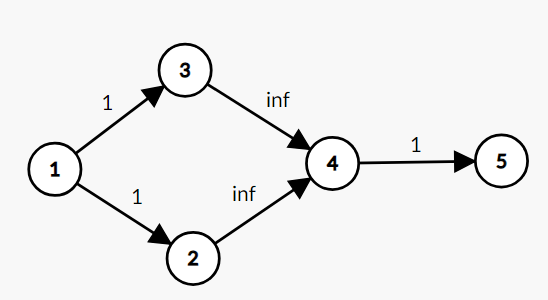
流之后：

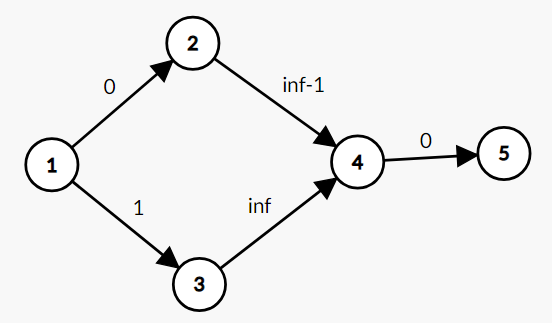
直接判断的话，会直接删两条边，然而最小割为 $1$。

正确做法：通过一个点是否有 $dis$ 值来判断是否与 $s$ 连通。因为我们考虑图中显然边 $(1,2)$ 是不能删的，这里仍存在这样一条路径：

$1 \Rightarrow 2 \Rightarrow 4 \Rightarrow 3$ ($4 \Rightarrow 3$ 为反向边)

所以要看 $dis$。

类型二二者取一问题

此类问题一般以把点集一分为二的形式出现。

P1361 小M的作物

首先仍然使用经典思路正难则反，先假设拿到所有的收益，再减去最小的不能取到的收益。

我们先不考虑共同种植的收益，那么做法应为对于每一个种子建出一个点，分别向源点，汇点（代表两块田地）连边权为 $a_i,b_i$ 的边，然后求最小割（割保证了一个点不能同时与源点和汇点连边，保证了题目里种子只能种在一块地上）。

我们考虑加入了合种收益，如果一组点能拿到合种收益，那么这些点一定要割在同一个点集内则合种收益与另一组的单种收益不共存，我们可以建模，对于 $A$ 的合种收益建一个点，向原点连边权为合种收益的边，向合种的点连边权为 inf 的边（保证其不会被割）,B 同理。最后跑流就行了。

P1791 [国家集训队] 人员雇佣

同样将一个点同时向源点和汇点连边，然后考虑如何处理共存。我们发现若两个点在一起会加 $E_{i,j}$，分开会减 $E_{i,j}$，那么差了 $2E_{i,j}$。我们可以将单点向源点连 $\sum E_{i,j}$ 的边，点之间连 $2E_{i,j}$ 的边，点向汇点连 $a_i$ 的边，流即可。

其实这种问题本质上就是在处理收益间的不共存问题。

无源汇最小割（Stoer-Wagner）

算法基于一个核心思想：最小割会将图分为两个点集，对于图中任意两个点 $s,t$，他们要么在同一点集内，要么在不同点集内。

先不考虑如何求无向图两个点之间的最小割，我们考虑先任意取两点 $s,t$，求出以他们为源汇的最小割，这时答案应等于求出的最小割以及 $s,t$ 在同一连通块内时的最小割的最小值。若 $s,t$ 在同一连通块内，由于是无向图，那么 $s$ 能到达的点 $t$ 也一定能到达，所以可以将 $s$ 与 $t$ 合并为一个点。

合并代码：（$g$ 数组为邻接矩阵）

for(int j=1;j<=n;j++){
	g[s][j]+=g[t][j],g[j][s]+=g[j][t];
}

合并之后，重复上述过程直至只剩下一个点，求出的所有最小割取最小即为答案。

求最小割方法：

建立集合 $A$，初始 $A = \varnothing$，定义 $dis(x,y)$ 为 $x$ 与 $y$ 之间的边权，若无边则返回 $0$，再定义权值函数 $W(i)=\sum\limits_{j \in A} dis(j,i)$。

下一步，不断将 $W$ 函数最大且不在 $A$ 之内的点加入 $A$ 之中（这个过程 $W$ 函数的值显然在不断变化），根据定理可知最后加入的点的 $W$ 值即为最小割。

定理的证明不需要掌握。

点击查看代码

#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define vi vector<int>
#define pb push_back
#define imp map<int,int>
#define debug printf("debug\n")
using namespace std;
const int N=605;
const ll inf=1e18;
int n,m,vis[N],del[N],ord[N],s,t;
ll ans=inf,w[N],g[N][N];
ll sw(int x){
    memset(w,0,sizeof(w));
    memset(vis,0,sizeof(vis));
    w[0]=-1;
    for(int i=1;i<=n-x+1;i++){
        int mx=0;
        for(int j=1;j<=n;j++){
            if(!del[j]&&!vis[j]&&w[j]>w[mx]) mx=j;
        }
        vis[mx]=1,ord[i]=mx;
        for(int j=1;j<=n;j++){
            if(!del[j]&&!vis[j]) w[j]+=g[mx][j];
        }
    }
    s=ord[n-x],t=ord[n-x+1];
    return w[t];
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1,x,y,z;i<=m;i++){
        scanf("%d%d%d",&x,&y,&z);
        g[x][y]+=z;g[y][x]+=z;
    }
    for(int i=1;i<n;i++){
        ans=min(ans,sw(i));
        del[t]=1;
        for(int j=1;j<=n;j++){
            g[s][j]+=g[t][j],g[j][s]+=g[j][t];
        }
    }
    printf("%lld\n",ans);
    return 0;
}

最小割树

在无向图上多次查询两点之间最小割。

先取任意两点求出最小割，该最小割一定将图分为两部分，我们将两个部分之间连一条边权为最小割的无向边，然后在两个部分之中递归此过程，直至分割出 $n$ 个点，此时形成一棵树即为最小割树，该树的性质为原图任意两点间的最小割等于这两点在树上的简单路径上的最小边权。

Pumping Stations

首先很容易求出最小割树。

然后我们考虑答案的上界，答案的上界即为最小割树所有边权的加和。若最小割树是一条链，将取点抽象为在最小割树上跳跃，此时按链的顺序走就可以得到该权值，且一定不会有更大的答案。但这只是特殊情况，能不能一定构造出一组这样的答案呢？答案是可以的。我们考虑一个最小割树中最短的边，显然该边断开后树会分为两部分，当我们的路径经过改边时，其权值一定为该边边权，而不经过权值有可能更大，由此可以想到一个贪心策略：我们假设当前最短边将树分为 $X,Y$ 两部分，我们先走完 $X$ 内所有点，最后一条路径经过最短边进入 $Y$，走完 $Y$ 中的点，对于一个部分内部，递归此流程进行分治，这样无疑保证了一定能取到理论最大值。当一个部分内只有一个点时，直接输出该点即可。

费用流

费用流的常规形式为最小（大）费用最大流，即在原图上每条边新增属性 $cost_i$，当一条边流量为 $flow_i$ 时，该边费用为 $flow_i \times cost_i$。最小费用最大流即是在最大流的前提下，找到费用最小的方案。

为了方便实现，我们采用 zkw 费用流算法。算法流程其实与 Dinic 算法类似。这里以横向对比的方式讲解最小费用最大流的算法流程。

首先，将 Dinic 算法的 bfs 部分改为一次从汇点开始的 SPFA，这样不仅沿用了 Dinic 将原图分层，判断连通性的功能，还可以求出一个点到汇点的最短路，方便选择最小费用。随后，和 Dinic 一样进行 dfs，但是要新增一个 $vis$ 数组，以防走环，搜索增广路时强行走最短边，但是这样就会同时封住一部分增广路，所以要每 dfs 一次后就将 $vis$ 清零再跑，直到 $s$ 与 $t$ 不连通。

一些细节：

反边的 $cost$ 要设为 $-c_i$。
此算法同样可以沿用当前弧优化

若要求最大费用最大流只需要将 SPFA 改成求最长路即可，或者将边权全部取反后跑最小费用最大流，最后答案再取反输出。

P2770 航空路线问题

问题可以抽象为在图上找两条只在起点和终点相交的路径，路径上点的数目最大。

首先这道题的限制，权值是基于点的，我们考虑将它拆点转化到边上，具体地，我们将点 $x$ 拆为 $x_1$ 与 $x_2$，从 $x_1$ 向 $x_2$ 连一条流量为 $1$，费用为 $1$ 的边，对于边 $(x,y)$，从 $x_2$ 向 $y_1$ 连边，流量 $1$，费用 $0$。

由于只需要两条路径，我们将源汇（易知源汇一定为最左与最右的点）也拆点，连流量为 $2$，费用为 $1$ 的边。跑一个最大费用最大流即可。

P4012 深海机器人问题

直接按照能走到的格子建图，特别之处在于第一次走有贡献，多次走能走但没有贡献，可以连两条边，一条流量为 $1$，费用为点权，另一条流量 $inf$，费用为 $0$，跑最大费用最大流。

P1251 餐巾计划问题

将餐巾看成流，由于脏餐巾和干净餐巾有区别（就像你不能把刚洗完的干净餐巾直接和脏餐巾一起扔着放那不动了）继续拆点，拆为早上和晚上两个点，按以下规则建图：

将源点向每一天早上连边，流量为 $r_i$，费用 $0$，代表产生了 $r_i$ 个脏餐巾。
将每一天晚上向汇点连边，流量为 $r_i$，费用 $0$，代表需要 $r_i$ 个干净餐巾。
将相邻两天早上连边，流量 $inf$，费用 $0$，表示脏餐巾摆烂放着。
将 $i$ 天的早上向第 $i+m$ 天连边，流量为 $inf$，费用为 $f$，快洗。
将 $i$ 天的早上向第 $i+n$ 天连边，流量为 $inf$，费用为 $s$，慢洗。
从源点向每天晚上连边，流量为 $inf$，费用为 $p$，买餐巾。

连边原则其实就是早上脏餐巾，晚上干净餐巾。

最后跑最小费用最大流。

P3358 最长k可重区间集问题

先离散化，然后考虑限制是“每个点至多被覆盖 $k$ 次”，进而考虑区间与区间之间的关系。区间与区间共两种关系：

相交
不相交

对于不相交的线段，我们一定是一起取，毕竟去了也不会导致某个点覆盖次数加了 $2$ 及以上，可以想到将这些边在网络中串联，而相交的线段就不能一起取，这样的话，很多个串联的线段链并联在一个网络中，具体的，对于一条线段，将其左端点向右端点连流量为 $1$，费用为 $len$ 的边，区间的右端点向下一个不相交线段的左端点连边，流量为 $1$，费用为 $0$。源汇连边均为流量 $1$，费用 $0$，注意初始流不给无穷大，要给 $k$，这是因为每条链相当于一层，最多叠 $k$ 层相当于最多取 $k$ 条链。

posted @ 2024-06-26 17:29 Aurora_Borealis 阅读(12) 评论(1) 编辑收藏举报

刷新页面返回顶部

Aurora_Borealis