可持久化 trie 学习笔记

由一个问题引入：

有一个数组\(a\)，\(q\) 次询问，每次给出 \(x,l,r\)，求 \(a_l\) 到 \(a_r\) 的数中与 \(x\) 最大的异或值。

显然如果没有 \(l,r\) 的限制这个问题可以用 \(01\) trie 解决。

加入 \(l,r\) 的限制后，这个方法显然不可行，我们考虑使用可持久化 trie 解决。

原理类似可持久化线段树。

先上一张盗的图：

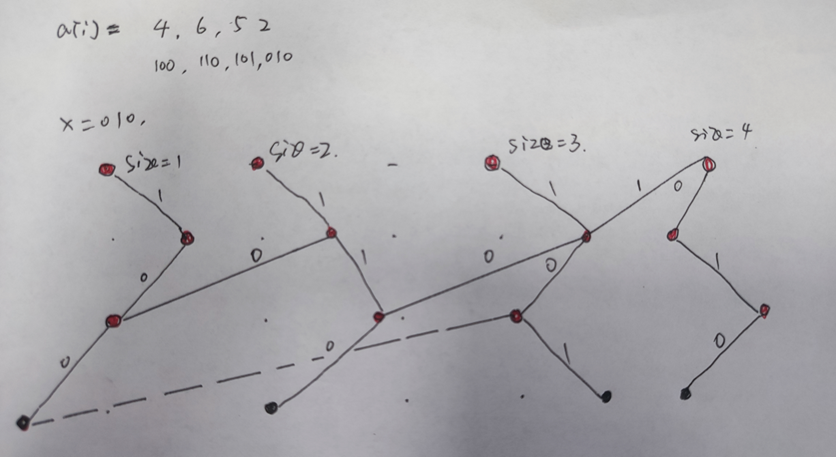
首先仍旧是从高位向低位依次处理。对于当前的数我们是一定要建立一条链的，对于链上每个点，将当前处理的这个数的下一位新建点，下一位外的连接到上一棵 trie 上。以 \(6\) 为例，第一个 \(1\) 直接建立，对于第二个 \(1\) 新建节点，同时将上一个节点的 \(0\) 道路连到上一颗 trie 上同一个位置的节点的 \(0\) 道路通向的点上。

插入操作就这么完成了。

接下来我们会归问题，如何排除区间外的数的干扰。

首先可知插入第 \(r\) 个数后的 trie 保存了 \(1\) 到 \(r\) 的信息。

我们再插入时维护每个子树的大小，在走一条道路时判断：若这个子树在 \(r\) 版本的 trie 上的体积等于在 \(l-1\) 版本上的体积，就意味着这条道路在 \(l\) 到 \(r\) 之间没有数可以走，这条路就不能走，反之则能走。剩下的和没有区间限制的情况一样。

查询也就完成了。

例题：P4735 最大异或和

首先是一个玩烂的套路：异或前缀和，处理出异或前缀和，问题转变为在一个区间内求出一个数异或 \(s_n \oplus x\)（一个定值）最大的值。

注意此时由于前缀和操作区间变为 \([l-1,r-1]\)。

最后就是直接套板子了，记得插入 \(0\)，记得特判 \(l=1\) 因为 \(l\) 会减成负数。

code:

点击查看代码

#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define debug cout<<"DEBUG"<<endl;
#define pb push_back
#define pii pair<int,int>
#define vi vector<int>
#define imp map<int,int>
using namespace std;
const int N=6e5+5;
int n,m,a[N],siz[N*30],rt[N],son[N*30][2],s[N],cnt;
void insert(int x,int y,int t,int k){
	if(t<0) return;
	int p=(k>>t)&1;
	son[x][p^1]=son[y][p^1];
	son[x][p]=++cnt;
	siz[son[x][p]]=siz[son[y][p]]+1;
	insert(son[x][p],son[y][p],t-1,k);
}
int query(int x,int y,int t,int k){
	if(t<0) return 0;
	int p=(k>>t)&1;
	if(siz[son[y][p^1]]>siz[son[x][p^1]]){
		return (1<<t)+query(son[x][p^1],son[y][p^1],t-1,k); 
	}else{
		return query(son[x][p],son[y][p],t-1,k);
	}
}
int main(){
	cin>>n>>m;
	rt[0]=++cnt;
	insert(1,0,25,0);
	for(int i=1;i<=n;i++){
		cin>>a[i];
		s[i]=s[i-1]^a[i];
		rt[i]=++cnt;
		insert(rt[i],rt[i-1],25,s[i]);
	}
	while(m--){
		char op;
		int l,r,x;
		cin>>op;
		if(op=='A'){
			cin>>x;
			n++;
			s[n]=s[n-1]^x;
			rt[n]=++cnt;
			insert(rt[n],rt[n-1],25,s[n]);
		}else{
			cin>>l>>r>>x;
			l--,r--;
			if(l==0){
				cout<<query(0,rt[r],25,x^s[n])<<"\n";
			}else{
				cout<<query(rt[l-1],rt[r],25,x^s[n])<<"\n";
			}
		}
	}
	return 0;
}