AC 自动机学习笔记

前置知识：KMP，trie。

一.自动机

这里的自动机都指有限状态自动机（DFA）。

一个 DFA 可以理解为一张有向图，由有限的状态（点），字母表，转移函数（边），开始状态与终止状态（起点，终点）组成。

AC 自动机就是一种在 trie 树的基础上，进行 KMP 算法中失配数组的计算，按照失配数组进一步建边，形成的有向图。也就是说，AC 自动机可以看成 trie 与 KMP 算法的结合体。

二.KMP 自动机

KMP 自动机可以看成构造简单些的 AC 自动机。

一个例子：请用一个字符串 \(s\) 构造一个 DFA，每个状态代表 \(s\) 的一个前缀，每次接收一个字符串 \(t\) ，终止于s最长的与t相同的后缀的前缀对应的状态。

本质是 \(t\) 在 \(s\) 上匹配的过程。设转移函数 \(trans(x_i,c)\) 表示状态 \(x\) 通过 \(c\) 字符的转移状态。

我们从前往后计算转移，则有：

\[trans_(x_i,c)=\begin{cases}x_{i+1}&s_{i+1}=c\\trans(fail_x,c)&s_{i+1} \neq c\end{cases} \]

三.AC 自动机

AC 自动机也可以看作多串的 KMP 自动机。

首先看一下这么做的必要性：

首先学过KMP的都知道，我们可以对于每个模式串跑 KMP，复杂度 \(O(n^2+nm)\)。

但处理多个串信息的特点也很容易想到 trie，但 trie 无法完成快速匹配，失配后只能从头比较，复杂度也不容乐观。那可不可以将 trie 加上失配数组呢？

假设我们有几个字符串：

bxwhl
lol
bxpb

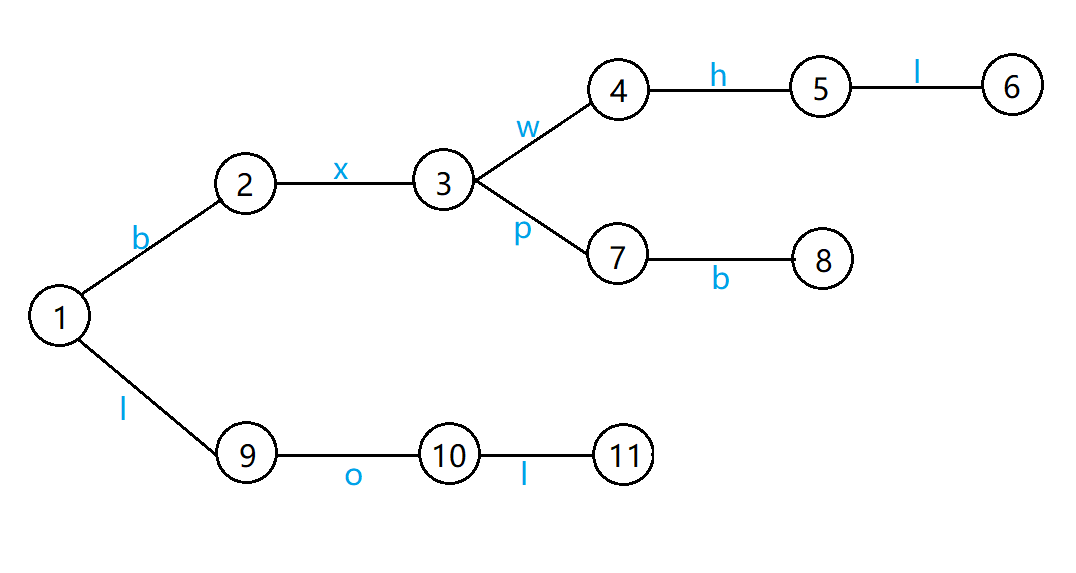
我们先建出 trie（后来发现编号错了QAQ,大家自行把所有编号减一吧）：

pSJYPxO.png

这里我将每个点设置一个 \(fail\) 指针，表示所有模式串前缀与当前状态匹配的最长后缀。还有另一种更通俗易懂的说法：设 \(fail_i\) 表示状态 \(x_i\) 失配后跳转到的状态，则他应指向 trie 上某一结点 \(p\)，\(x_p\) 对应的前缀最长且恰好为 \(x_i\) 的后缀。

过程如下：

  • 首先 \(fail_0=0\)。

  • 然后 BFS 整棵树，因为 \(fail\) 指针一定指向深度更浅的点（显然）；

  • 对于每个点 \(x\)，访问其父节点 \(fail\) 指针指向的点，检查该点的儿子是否存在与 \(x\) 相同的点，如果相同，将指针指向该点，否则继续访问新的父节点的 \(fail\) 指针。

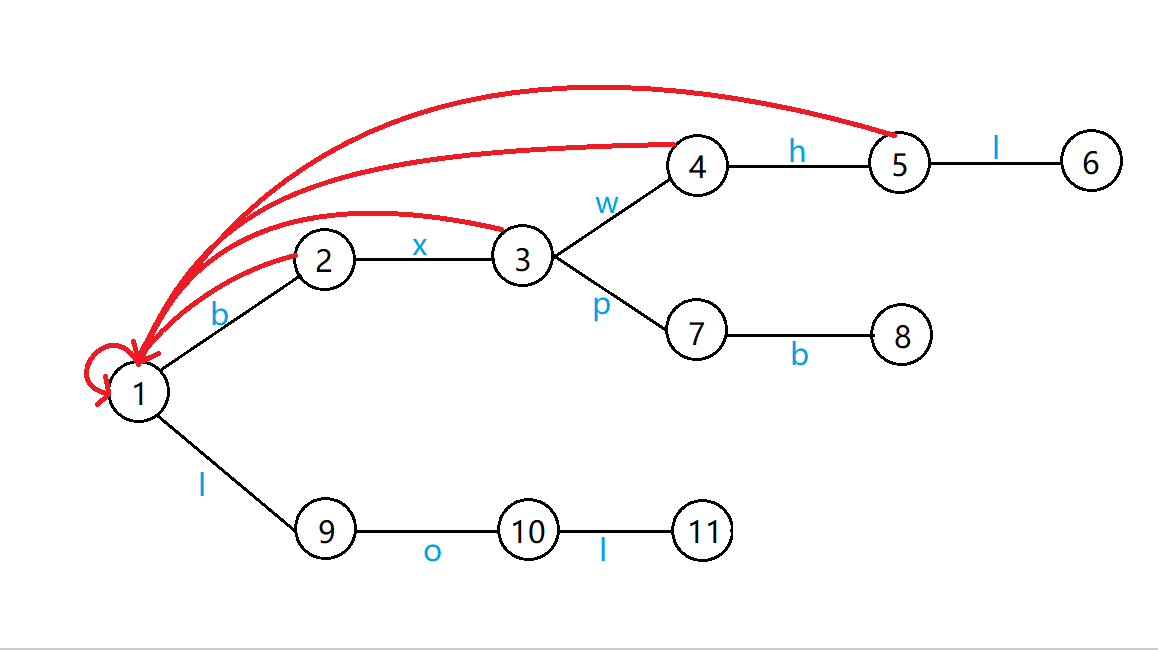
以串bxwhl举例子，展示一下处理过程。

pSJqYJH.png

如图，对于bxwh，都没有出现匹配的后缀，所以都指向节点 \(1\)。

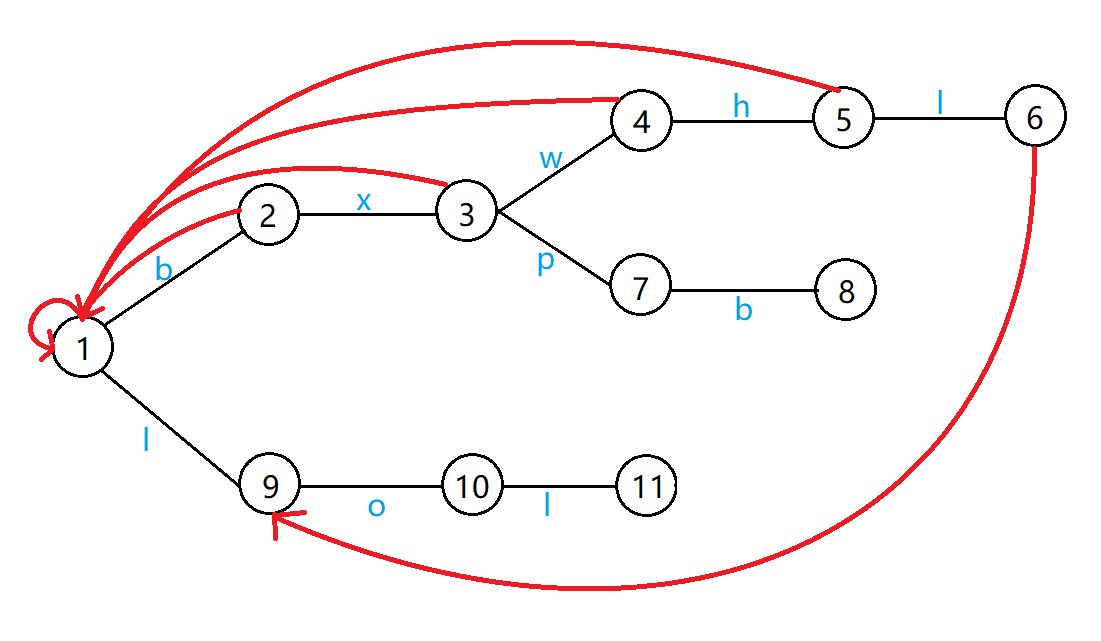
pSJqwOP.png

对于 l，先跳转其父节点 \(5\) 的 \(fail\) 指针,跳转到 \(1\)，发现存在一条 l 边指向节点 \(9\)，所以 \(6\) 指向 \(9\)。其他节点同理。

下一步，仍设转移函数 \(tran(x_i,c)\) ，我们从前往后计算转移，则有（没错和KMP 自动机的一模一样）：

\[trans_(x_i,c)=\begin{cases}x_{i+1}&s_{i+1}=c\\trans(fail_x,c)&s_{i+1} \neq c\end{cases} \]

特别地，有初始状态（空前缀）设为 \(x_0\)，除 \(trans(x_0,s_1)\) 外指向它自己。容易看出，此时字典树已经变成了字典图。

然后我们这时可以回归例题了：

首先，对于模式串建出 AC 自动机，用文本串在上面跑。

例题：

posted @ 2023-01-22 17:27  Aurora_Borealis  阅读(42)  评论(0)  编辑  收藏  举报