分层图最短路学习笔记

一.定义

分层图最短路，是指在可以进行分层图的图上解决最短路问题。

一般模型为：在图上有 \(k\) 次机会直接经过一条边（边权降低为 \(0\)）

二.原理

以P2939举例：

首先考虑样例简单情况（ \(k=1\) ）：

4 4 1 
1 2 10 
2 4 10 
1 3 1 
3 4 100 

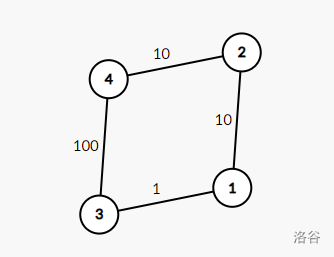
此时可以建一个与原图对称的图，用可以走的 $ 0 $ 边将两个图连接起来。

最后在新图上跑一遍最短路，取终点dis与终点对称点dis最小值即是答案。（可以自己想一想为什么）

这种做法同样可以推广到 \(k=n\) 的情况，建 \(k+1\) 层图即可。

4 3 2
0 1 100
1 2 100
2 3 100

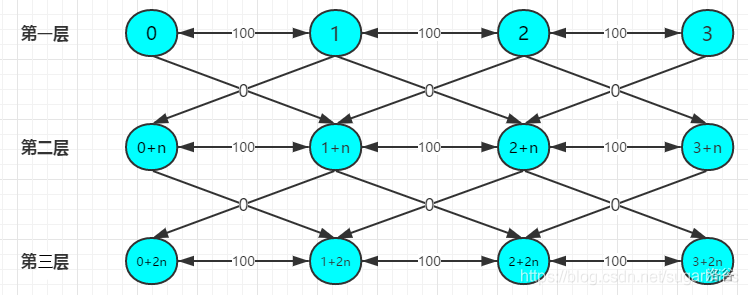
(引用自这里，侵删)

三.注意事项

由于分层图最短路要建多层图，数组大小要开得更大。

上图为不开大数组或数组大小计算错误的下场。

当图为无向图，有 \(n\) 个点，\(m\) 条边，需要建 \(k\) 层图。

当只建一层图时，\(N=n\), \(M=2m\)。

在建 \(k\) 层图时，先考虑有多少个点：

一层图 \(n\) 个点，\(k\) 层图 \(kn\)个点，没有任何疑义。

边稍微复杂点，但难度也不大：

先算每层图内部的边，一层图 \(2m\) 条边，\(k\) 层图 \(2km\)条边。

找规律，可以发现每两层图之间需要 \(2n-2\) 条边，\(k\) 层图之间需 \(2nk-2n-2n+2\) 条边。

则共需 \(2nk-2n+2km-2k+2\) 条边，写得好看点就是 \(2k(n+m)-2(n+k)+2\) 条边。

正常分层图最短路题是不会卡内存的（？），用 \(2k(n+m)\) 算就行，卡空间还是老老实实一点一点算吧。

结论：当运用分层图最短路时，邻接表中 \(N=kn\), \(M=2k(n+m)-2(n+k)+2\)。

练习题目：

[BJWC2012]冻结

[USACO08JAN]Telephone Lines S

[NOIP2009 提高组] 最优贸易

【好题】[APIO2013] 机器人