分治算法（C语言）
一、棋盘覆盖问题
1、问题
2、分析
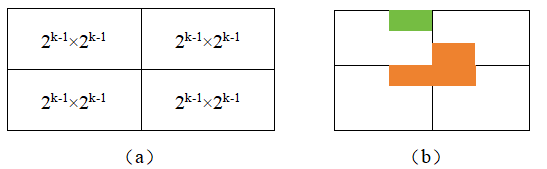
（1）当k>0时，将2k×2k棋盘分割为4个（2k-1）×（2k-1）子棋盘，如图（a）所示。每一次分解，都将原本大小的棋盘，划分为四份，即行号和列号各自缩减一半。
（2）特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。
（3）为将无特殊方格子棋盘转化为特殊棋盘，可以用一个骨牌覆盖3个较小棋盘的会合处，如图（b）所示，从而将原问题转化为4个较小规模的棋盘覆盖问题。即：将骨牌的三个部分分别仿作特殊方格子
（4）递归地使用这种分割，直至棋盘简化为棋盘1×1
3、代码分析
（1）入口参数
tr，tc表示当前棋盘的左上角的坐标（tr，tc）
dr，dc表示特殊方格的坐标（dr，dc）
（2）判断特殊方块在相对于当前棋盘的中心（tr+s，tr+s）哪个位置：
如果在左上，即有（dr<tr+s，dc<tc+s），若不在，则将（tr+s-1，tc+s-1）涂黑
如果在左下，即有（dr≥tr+s，dc<tc+s），若不在，则将（tr+s，tc+s-1）涂黑
如果在右上，即有（dr<tr+s，dc≥tc+s），若不在，则将（tr+s-1，tc+s）涂黑
如果在右上，即有（dr≥tr+s，dc≥tc+s），若不在，则将（tr+s，tc+s）涂黑
如果在，则传入对应特殊方格位置，并缩小规模
4、代码实现
/*棋盘覆盖问题(分治算法)*/
#include<iostream>
#include<algorithm>
using namespace std;
//L型骨牌的编号(递增)
int title=65;
//棋盘
int Board[10][10];
/*函数形参说明：
tr：当前棋盘左上角的行号
tc：当前棋盘左上角的列号
dr：当前特殊方格所在的行号
dc：当前特殊方格所在的列号*/
void ChessBoard(int tr,int tc,int dr,int dc,int size) {
if(size == 1)
return;
/*编号加1,且每执行1次，即将原本的棋盘划分成原来的1/4*/
int t=title++;
int s=size/2;
/*判断特殊方块的位置*/
//左上
if(dr<tr+s && dc<tc+s)
ChessBoard(tr,tc,dr,dc,s);
else {
Board[tr+s-1][tc+s-1]=t;
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//右上
if(dr<tr+s && dc>=tc+s)
ChessBoard(tr,tc+s,dr,dc,s);
else {
Board[tr+s-1][tc+s]=t;
ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//左下
if(dr>=tr+s && dc<tc+s)
ChessBoard(tr+s,tc,dr,dc,s);
else {
Board[tr+s][tc+s-1]=t;
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//右下
if(dr>=tr+s && dc>=tc+s)
ChessBoard(tr+s,tc+s,dr,dc,s);
else {
Board[tr+s][tc+s]=t;
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main() {
int size=8;
int index_x=3;
int index_y=4;
ChessBoard(0,0,index_x-1,index_y-1,size);
for(int i=0;i<size;i++){
for(int j=0;j<size;j++)
cout << (char)Board[i][j] << ' ';
cout << endl;
}
system("pause");
return 1;
}
二、循环日程问题
1、问题
设有n=2k个选手要进行网球循环赛，设计一个满足以下要求的比赛日程表：
（1）每个选手必须与其他n-1个选手各赛一次
（2）每个选手一天只能比赛一次
（3）循环赛在n-1天结束
2、分析
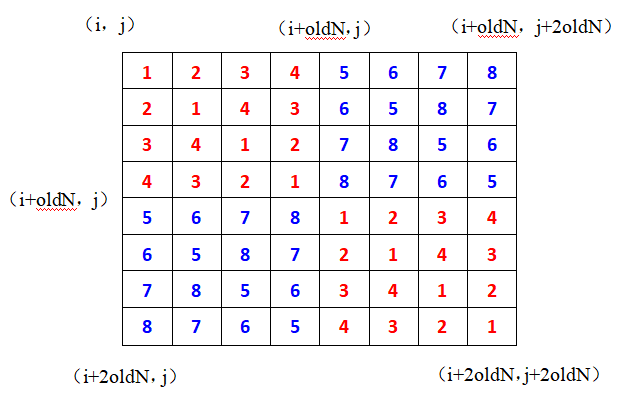
规律：（1）左上 = 右下 左下 = 右上
（2）左下的值 = 左上的值 + oldN （n0 = 2，n = oldNnum）
3、代码分析
按照左下、右上、右下的遍历次序进行遍历oldN=n，n=oldN*2
（1）左下，行号遍历范围为[oldN+1，n]，列号遍历范围为[1，oldN]
（2）右上，行号遍历范围为[1，oldN]，列号遍历范围为[oldN+1，n]
（3）右下，行号遍历范围为[oldN+1，n]，列号遍历范围为[oldN+1，n]
4、代码实现
/*循环日程问题(分治算法)*/
#include<iostream>
#include<algorithm>
using namespace std;
int a[1000][1000];
/* (i,j) (i,j+oldN) (i,j+2oldN)
(i+oldN,j) (i+oldN,j) (i+2oldN,j+2oldN)*/
void Plan(int k) {
int i,j,oldN,n;
int num=1;
/*原始规模为2，每次规模行和列均‘*2’*/
n=2;
a[1][1]=1;
a[1][2]=2;
a[2][1]=2;
a[2][2]=1;
/*迭代处理‘2^k’中情况*/
while(num<k) {
oldN=n;
//右区间的边界
n=n*2;
//左下角
for(i=oldN+1;i<=n;i++)
for(j=1;j<=oldN;j++)
a[i][j]=a[i-oldN][j]+oldN;
//右上角(与左下角一致)
for(i=1;i<=oldN;i++)
for(j=oldN+1;j<=n;j++)
a[i][j]=a[i+oldN][j-oldN];
//右下角(与左上角一致)
for(i=oldN+1;i<=n;i++)
for(j=oldN+1;j<=n;j++)
a[i][j]=a[i-oldN][j-oldN];
num++;
}
}
int main() {
int k=3;
Plan(k);
int num=1;
for(int i=1;i<=k;i++)
num *= 2;
for(int i=1;i<=num;i++) {
for(int j=1;j<=num;j++) {
cout << a[i][j] << "\t";
}
cout << endl;
}
system("pause");
return 1;
}
