NOIp2018普及组初赛解题报告
先附上答案:

今年的题目有点诡异,我们来看看怎么做!
一、选择题
- D。第一题水题,打印机肯定是输出设备喽。
- D。第二题涉及到了进制转换,我们可以都转换为十进制,或只算末位数。发现D末位是9,其他都是7。
- D。这是常识:1GB=1024KB=1024*1024B。
- B。这题我也是瞎猜的,因为手机上我们打开Wi-Fi的按钮下面,好像有WAN什么。查过资料后:广域网 - Wide Area Network - WAN。
- B。这题要积累了,是1984年创办的。
- A。以前貌似也看过这道题。其实就是ASDFasdf的循环,每八个一循环,把要求的数字mod 8就知道是哪个了。
- A。由于是k>1的叉树,所以二叉树也肯定满足。只需想到满二叉树的节点个数与深度的关系,就可求出公式。
- A。基数排序不就是桶排吗,直接放入桶里,肯定没有比较的过程啦。
- A。C与D肯定不是,时间复杂度一般都是最坏情况,猜猜也是要向上取整。
- B。送分题,前几年貌似也出现过。
- A。分类讨论求出是6个。图解:
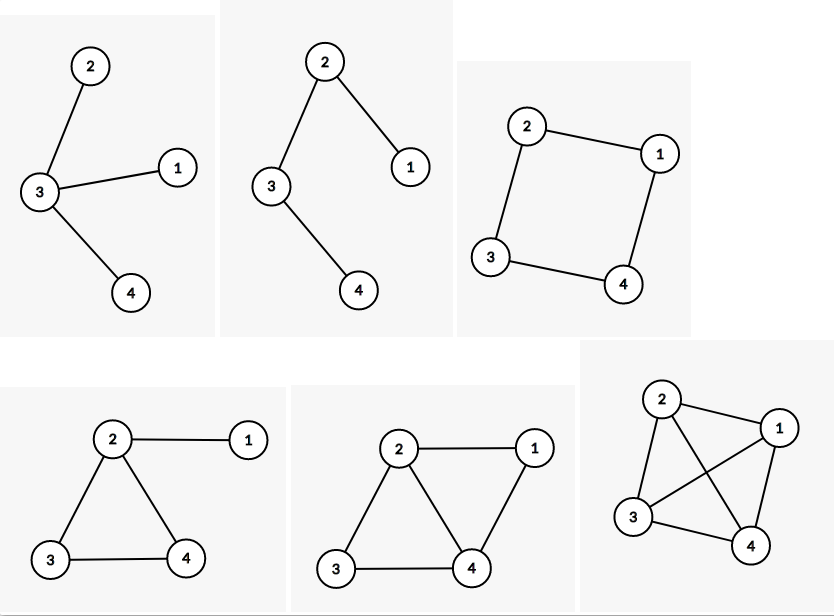
- B。注意空集。
- B。2的倍数有4999个,5的倍数有1999个,除去10(2和5的公倍数)999个,加上10000这一个数,不互质的就是6000个,互质的就是10000-6000=4000个。
- B。蒟蒻看了会模拟,大佬看了这是状压DP。
- B。很容易看出,这是栈的操作。
二、问题求解
- 第一道不是很难,其实就是小学奥数。只要假设某个人说的是真的,然后判断是否符合所有条件。
- 第二题可以枚举8的位置,即可解出答案。但要注意最后要加个2(因为2000~2018中有2个有8的)。
三、写结果
- 不难发现,就是将所有大写的字母,按字典序变成了后一个字母,但Z要变成a(按ASCLL码表中的顺序)。输出:RuanHuoMianTai。
- 读题意得知,要求 0~15 中,有几个数的平方mod 15==1。耐心模拟后,算出是4。输出:4。
- 考试时,我用的是暴力模拟,真的是累死我。后来从同学那里得知,可以用表格找规律。如下:
输出:8。0 1 2 3 4 5 6 0 0 1 2 3 4 5 6 1 1 0 3 2 5 4 7 2 2 -1 4 1 6 3 8 3 0 1 2 3 4 5 6 4 1 0 3 2 5 4 7 5 2 -1 4 1 6 3 8 - 模拟。输出:6。
四、完善程序
- 是求最大公约数之和。最大公约数求解有递归公式:return b==0?a:a%b; 其他直接按题意说的做即可。
- 第2题,双向链表求排序,没学过,只能用最简单粗暴的方法,那就是:看对称,(3)(4)小题就能迎刃而解。至于(1),如果直接cin>>a[i],肯定不会多定义一个x,这么做一定是有意图的。想半天,觉得应该是a[x]=i,a数组,记录的是x的位置。第(2)小空,不难想出是i+1。第(5)小空,按题意看出应该是求右边,所以输出R数组即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号