CTF练习week02
1. base64
下载附件

Base64解密
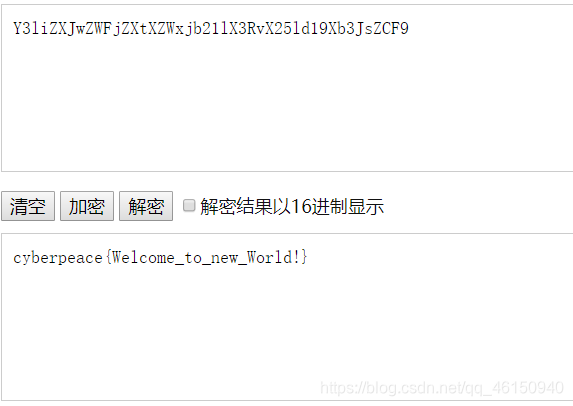
2. Caesar

下载附件

凯撒密码解密,当位移为12时得到flag
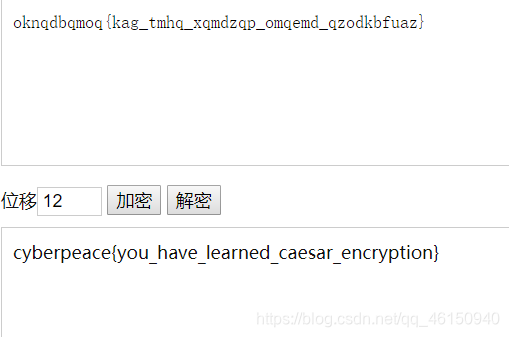
3. Morse

下载附件
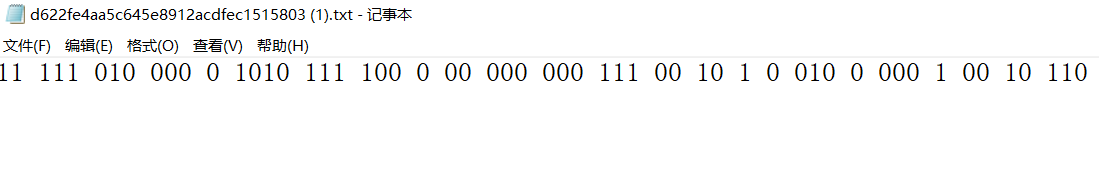
摩斯密码 1替换成-,0替换成.
运用一个简单脚本实现转化
morse="11 111 010 000 0 1010 111 100 0 00 000 000 111 00 10 1 0 010 0 000 1 00 10 110"
morse=morse.replace("1","-")
morse=morse.replace("0",".")
print (morse)
运行脚本得到
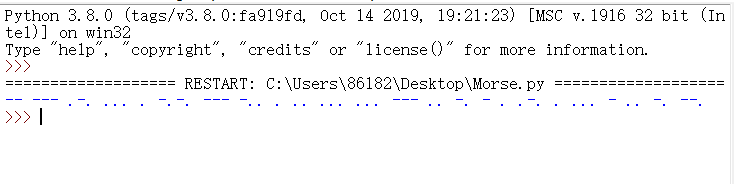
摩斯密码解密得到flag
4. 不仅仅是Morse
下载附件

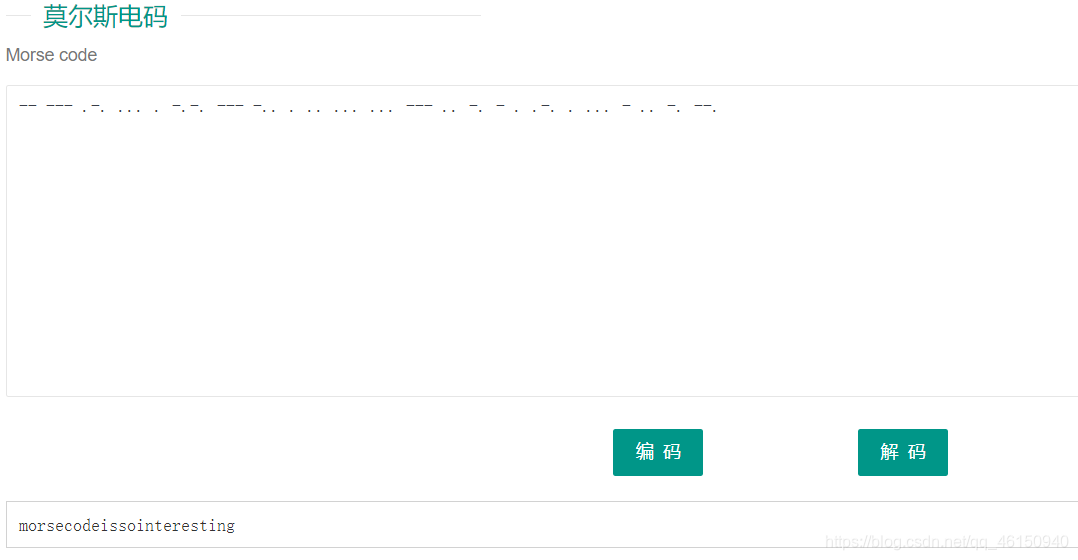
用摩斯密码工具将密文转成字母
MAYBEHAVEANOTHERDECODEHHHHAAAAABAABBBAABBAAAAAAAABAABABAAAAAAABBABAAABBAAABBAABAAAABABAABAAABBABAAABAAABAABABBAABBBABAAABABABBAAABBABAAABAABAABAAAABBABBAABBAABAABAAABAABAABAABABAABBABAAAABBABAABBA

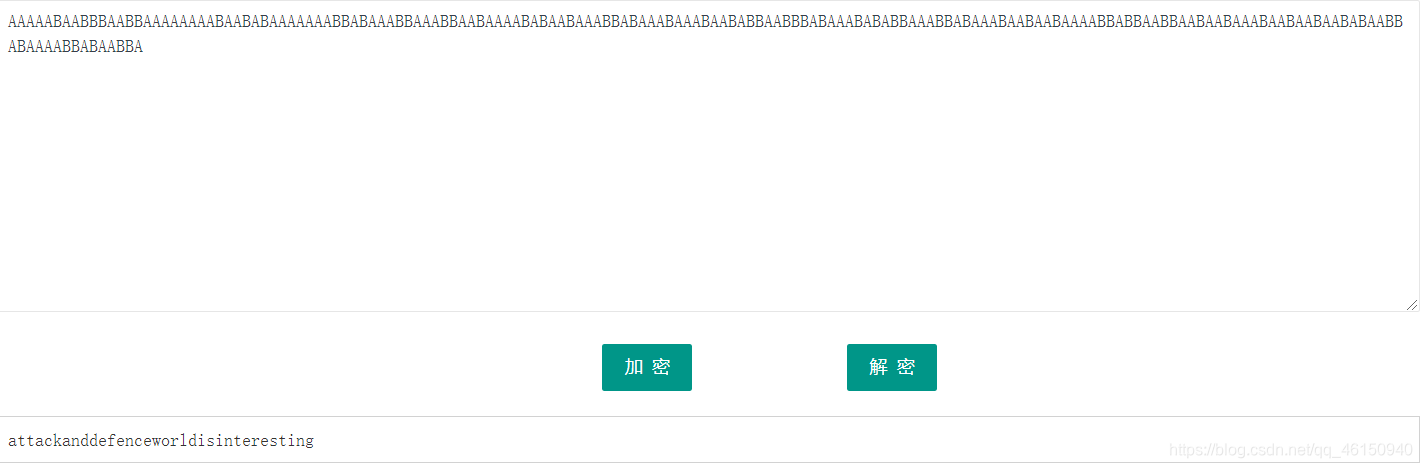
后面部分全是A和B的组合,想到培根加密
AAAAABAABBBAABBAAAAAAAABAABABAAAAAAABBABAAABBAAABBAABAAAABABAABAAABBABAAABAAABAABABBAABBBABAAABABABBAAABBABAAABAABAABAAAABBABBAABBAABAABAAABAABAABAABABAABBABAAAABBABAABBA
培根密码解密得到flag
5. 混合编码

下载附件

看到字符串最后面的==,猜出来是Base64,Base64解密
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw
Unicode 解码,得到
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw
再base64解码
/119/101/108/99/111/109/101/116/111/97/116/116/97/99/107/97/110/100/100/101/102/101/110/99/101/119/111/114/108/100
ascll码转化为字母,得到flag
welcometoattackanddefenceworld
6. 幂数加密
下载附件

百度了一下

将原文档处理了一下

flag为cyberpeace{WELLDONE}
附上大佬的脚本
s = '8842101220480224404014224202480122 '
s1 = s.split('0')
for s2 in s1:
sum=0
for i in range(len(s2)):
sum=sum+int(s2[i] )
print(str.upper(chr(ord('a')+sum-1)) ,end='')
运行脚本得到
WELLDON
7. Railfence
根据题目提示,发现可能是栅栏密码,并且栏数为5,下载附件

附件是已经被加密过的密文, 尝试了栅栏解密没有得到flag。查了一下,发现是栅栏密码的变种,W型加密。

flag格式为cyberpeace{xxxxxxxxxx},前面知道了栏数为5,整理一下密文

排列成W型
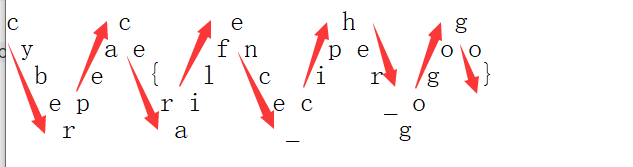
按照箭头方向读取字符串,得到flag为cyberpeace{railfence_cipher_gogogo}
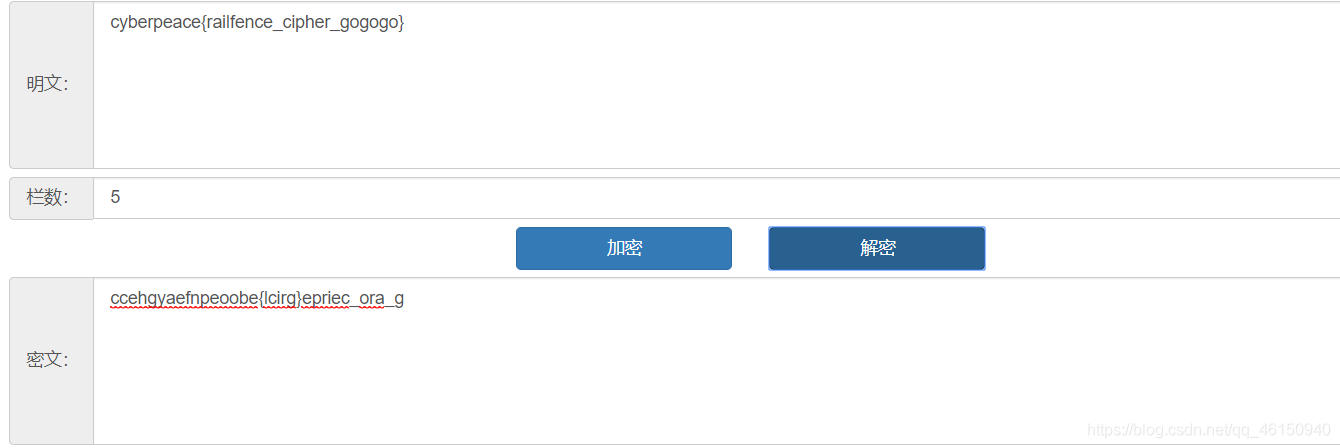
上面的步骤比较麻烦,也可以用在线工具解题
栅栏密码加密/解密【W型】
8. easy_RSA

下载附件

RSA算法
1.随机选择两个不相等的质数p和q。
2.计算p和q的乘积n(n=pq),n的长度就是密钥长度。
3.计算n的欧拉函数φ(n): φ(n) = (p-1)(q-1)
4.随机选择一个整数e,也就是公钥当中用来加密的那个数字 条件是1< e < φ(n),且e与φ(n) 互质。
5.计算e对于φ(n)的模反元素d。也就是密钥当中用来解密的那个数字
所谓"模反元素"就是指有一个整数d,可以使得ed被φ(n)除的余数为1,ed ≡1 (mod φ(n)) 。
6.将n和e封装成公钥,n和d封装成私钥,(n,e),(n,d)就是密钥对。
7.首先对明文进行比特串分组,使得每个分组对应的十进制数小于n,然后依次对每个分组m做一次加密,所有分组的密文构成的序列就是原始消息的加密结果,即m满足0<=m<n,则加密算法为:
c≡ m^e mod n; c为密文,且0<=c<n。
对于密文0<=c<n,解密算法为:
m≡ c^d mod n;
贴上大佬的脚本
def exgcd(a, n):
if n == 0:
return 1, 0
else:
x, y = exgcd(n, a % n)
x, y = y, x - (a // n) * y
return x, y
def getReverse(a, n):
re, y = exgcd(a, n)
while(re < 0):
re += n
return re
if __name__ == "__main__":
p = 473398607161
q = 4511491
e = 17
d = getReverse(e, (p - 1)*(q - 1))
print('d = ' + str(d))
运行脚本
d = 125631357777427553


 浙公网安备 33010602011771号
浙公网安备 33010602011771号