杂题选讲1&2

把序列排序后
问题转化为子序列两两之间的异或和大于等于k
用户\(Trie\)树优化\(dp\)
因为不满足单调性所以不能用二分来优化

\(ans=\sum_{i=1}^{n}n%i\)
\(ans=\sum_{i=1}^{n}(n-n/i*i)\)
\(ans=n^2-\sum_{i=1}^{n}i*(n/i)\)
从实际含义入手
\(ans=n^2-\sum_{i=1}^{n}d1(i)\)
\((dk(i)=\sum_{j|i}j^k)\)
线性预处理即可
复杂度\(O(N+T)\)

原先做\(SA\)的题时用过这个套路
枚举长度\(len*2\),每隔\(len\)插一个点
这样对于相邻两个关键点求出最长公共前缀和最长公共后缀
那么答案串便可以在这个区间里滚动
类似哈希的去求贡献
假如\(S[i+1]=0\)，根据平方串的性质可以让\(H[i]=0\)来解决前导零

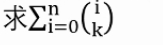
其中ki给定
考虑对于每个组再分组
每个组被\(k_i\)个人分成了\(k_i+1\)个小组
发现有\(k_i\)个小组大于\(0，1\)个小组可能等于\(0\)
为了统一化，让前\(k_i\)个小组不包含被选中的人，
条件都变成每个小组非负
直接组合数计算即可

转化为其他组在\(1\)之前被丢掉的概率之和
\(i\)的贡献便是\(\frac{A[i]}{A[i]+A[1]}\)

是原来一道提答题的部分分
对于每个数\(x\)它自主删的概率便是\(\frac{1}{d(x)}\)
加和便是答案
这道题需要用到\(min_25\)筛

神奇的期望线性性！！
设\(E_G\)代表每拿一个蓝球绿球被拿的期望个数
\(E_G=(E_G+1)*\frac{G}{B+G}\)
\(E_G=\frac{G}{B}\)
所以绿球的贡献便是\(\frac{GK}{B}\)
对于每个红球可以分开考虑
它不被拿出的概率\(P_R=(\frac{1}{B+1})^k\)
红球的贡献便是\(E_R=R*(1-P_R)\)

考虑预处理出可能对答案造成贡献的点对
对于一个右端点\(r\)，左端点\(x,y\)
一定满足，\(a_x<a_y\)
并且满足\(a_r-a_y<a_y-a_x\)
即\(2*(a_r-a_y)<a_r-a_x\)
也就是说差值至少变为了一半
所以对于一个确定的右段点，最多有\(log\)个
拿数据结构去求出并且维护即可

考虑对每个\(|i|\)所在的两个变量之间连一条边(一个除外)
那么每个联通块只会是链或者环
链就用\(dp\)来搞，环的话就枚举断开的取值来变成链

考虑容斥，先钦定一些边不被覆盖
之后每个联通块两两匹配
设\(dp[i][j]\)代表\(i\)的子树大小为\(j\)的方案数
复杂度\(O(n^2)\)
钦定的时候加一个\(-1\)的系数便可以只做一次\(dp\)

对于每个颜色整一个\(a[i]\)次的多项式
其中第\(j\)项代表至多\(j\)个块的方案数:\(C(a[i]-1,j-1)/j!\)
之后用\(FFT\)再容斥一下求出总的方案数
就可以\(O(1)\)的回答问题啦

设\(f[i]\)代表\(i\)行\(m\)列每列都不同的方案数
设\(g[i]\)代表\(i\)行\(m\)列每行都不同，每列都不同的方案数
则有:
\(f[i]=A_{C^n}^{m}\)

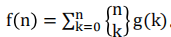
由斯特林反演得到:


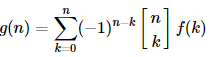
设\(g[i]\)代表恰好有\(i\)个联通块的方案数
设\(f[i]\)代表\(i\)划分下的总方案数

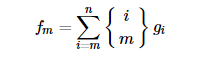
现在的问题便是求\(f[i]\)
\(f\)的限制是不同集合之间不能有连边
所以枚举子集划分，设\(x_i\)代表\(i\)这个图是否选
所以便可以列出若干个异或方程
高斯消元一下求出主元的个数\(cnt\)
主元不可以随便选，其他的图可以，贡献就是\(2^{S-cnt}\)
最后斯特林反演一下便可以得到\(ans=g(1)\)了