DP

考虑枚举root那么所有操作点对一定不是祖孙关系

设f(x)代表x子树中能消掉的最大对数

sum(x)代表x子树内dis之和

max(x)代表x的儿子的最大sum

那么$1>sum-max<max f(x)=sum-max+{0=<k<=f(u)|k*2<=max*2-sum}$

剩下$2max-sum$个点

其中u是max所在的点

$2>sum-max>=max f(x)=sum/2$下取整

剩下1/0个点没有被消

最后假如$roo$t合法当且仅当sum(x)是偶数且f(root)=sum(x)\2

时间复杂度$O(n^2)$

$$ans=\sum_{i=1}^{9}i*c(i)$$

c(i)代表i数字的贡献

这里考虑把i*c(i)转化成在每个小于等于i的地方累加c(i)，即

$$ans=\sum_{i=1}^{9}\sum_{j=i}^{9}c(j)$$

后面的一个求和取决于有多少个大于等于i的有多少个

直接数位dp出来即可

 

 

对于每个点求出上限值

那么高度为h的限制只能由上限为h的点贡献

所以枚举h把上限为h的拿出来dp即可

n很大不能直接做感觉会很麻烦

 

其实这个思路在原来的题中出现过只是没有命名

以下的题目是笛卡尔树dp

 

 

 

 

先把权值离散化

设dp[i][j][k]代表[i,j]的最小值是k的最大花费

这里的最大花费只包含[i,j]完全覆盖的区间

枚举最小值k的位置x

$dp[i][j][k]=max(dp[i][x-1][p>=k]+dp[x+1][i][q>=k]+calc(i,j,k))$

很常见的笛卡尔树dp的思路？？？

 

考虑每次消掉一个H最小的当成根建出树来

那么设dp[i][j]代表i的子树中放j个的方案数

先子树合并之后考虑当前节点x的贡献

惊奇地发现是一个矩阵：

行：H[x]

列：size[x]-j

便可以做到简单统计

 

假如是一个矩阵的话

考虑逐行处理

假如某一行是黑白相间，那么下一行可以全部反转或者继承

否则只能是反转

这个是比较显然的

套上笛卡尔树解决即可变为矩阵

 

这样的问题一般的套路便是从大到小加入

考虑把原序列排序后差分一下

那么发现加入的时候贡献系数就是两边的空地的个数

所以现在我们就不关注端点是什么了

dp[i][j][k][0/1][0/1]代表到第i个元素，贡献和为j，段数为k，左右端点是否覆盖的方案数

分为新建/合并/扩展dp即可

(个人感觉差分那里多此一举，类似赤壁那题从大到小加入的时候绝对值就已经拆开了)

 

接下来便是dp套dp

 

设$f[i][j]$代表$S$的前$i$位与$T$的前$j$位的$LCS$

（这里的$LCS$是最长公共子序列，而不是最长公共后缀，第一次看的时候懵逼了好久）

转移:

$1>S[i]=T[j]\ \ f[i][j]=f[i-1][j-1]+1$

$2>S[i]!=T[j]\ \ f[i][j]=max(f[i][j-1],f[i-1][j])$

显然$f[i][j-1]=<f[i][j]<=f[i][j-1]+1$

那么可以状压每个$j$是否是$f[i][j-1]+1$

所以考虑设$g[i][j]$代表到了第$i$位，$f$的状态是$j$的方案数

预处理出每个状态之后加字符到达的状态便可以之后$O(1)$转移

复杂度$O(m2^n)$

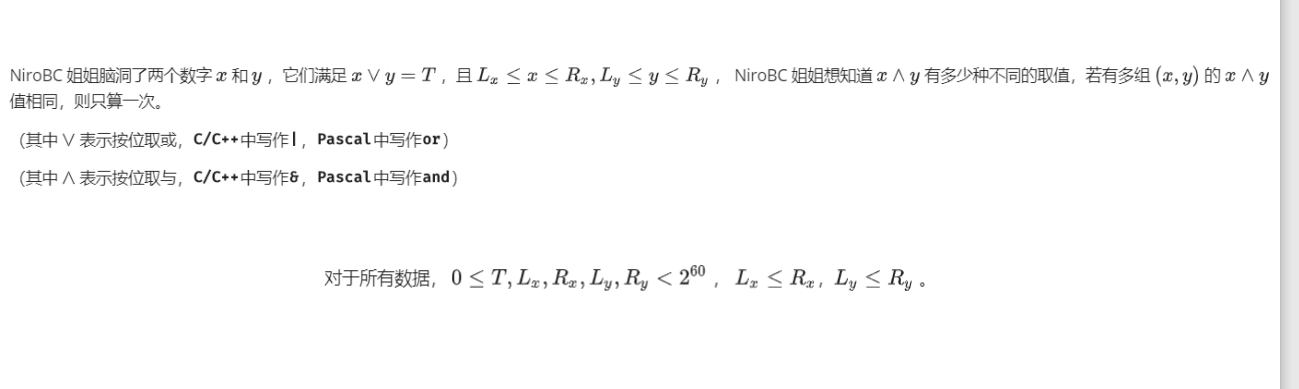
设$dp[i][j][k][l][r]$代表考虑到了第$i$位，

$x$与$L_x$,$R_x$的关系是$i$,$j$,$y$与$L_y,R_y$的关系是$l$,$r$是否可行

转移的话就是枚举x&y的这一位是0/1

根据T的这一位来进行转移