网络流总结(二)最小割

最大流最小割定理

对于一个网络流图$D=(V,E)$的一个可行流$f$，下述三个命题等价:

1>$f$是最大流

2>残余网络$G_f$不存在增广路

3>存在一个割$c$使得$c=f$

证明几乎是照搬的$rvalue$学长的

首先证明1->2:

假设残余网络中仍存在增广路，那么一定可以继续增光增加流量，则f不是最大流，与1命题矛盾

所以若f是最大流，则残余网络中一定不存在增广路

2->3:

设点集$L$为残余网络中$S$可以到达的点，$R$为$L$的补集，

那么对于$x\in{L}$，$y\in{R}$，一定有$f(x,y)=c(x,y)$

所以$f(S,T)=\sum{}{}{f(x,y)}=\sum{}{}{c(x,y)}=C(S,T)$，即$c=f$

3->1:

因为割一定大于等于流，所以此时的$c$一定是最小割，$f$一定是最大流

---

T1切糕

题目大意:给定n*m的位置，每个位置确定一个高度并获得相应的权值，相邻格子的高度差不能超过D，最大化权值和

首先考虑当没有高度限制时该怎么做:

裆燃是每个位置取$max$辣，但是假如不会取$max$，只会网络流该怎么办呢？

多加一层，每个位置都挂出一条链，链上的权值为每个位置各个高度的权值，求出最小割便是答案

如果加上高度限制，对于一对相邻位置$L$,$R$，假设$hL>hR$

我们需要让$L$选择$x$时$R$不能选择$x-D$以下的部分，也就是说当$R$选择$x-D$以下部分时需要有一条路径从可以联通$S-T$且$cap=INF$

考虑连边$(Lx,R_x-D,INF)$，恰好可以满足上述要求，问题得到了解决

---

 

T2狼抓兔子

题目描述

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.

输入格式

第一行为N,M.表示网格的大小，N,M均小于等于1000.
接下来分三部分
第一部分共N行，每行M-1个数，表示横向道路的权值.
第二部分共N-1行，每行M个数，表示纵向道路的权值.
第三部分共N-1行，每行M-1个数，表示斜向道路的权值.
输入文件保证不超过10M

输出格式

输出一个整数，表示参与伏击的狼的最小数量.

直接求最小割会$T$(除非打$ISAP$)，我们需要一种更好的方案求出这张图的最小割...

平面图转对偶图：

 

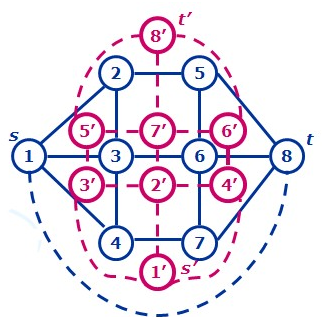
对于红色的新图，我们发现其每一条$S'->T'$的路径便对应着原图中的一个最小割，

建出图来直接跑$DJ$求最短路也就是最小割即可

---

 

 T3海拔

题目描述

输入格式

输出格式

题目中西北角是0,东南角是1,所以海拔不是0就是1，并且0,1的点一定分别是一个联通块

所以答案就是西北到东南的最小割，这样就和上一道题一样了

upd:

刚刚发现海拔可以是小数，但是在这种情况下海拔依然不是0就是1

因为如果出现小数相当于对原图进行了多次割

即$ans=\sum\limits_{i=1}^{n}a_i*x_i$，其中$\sum\limits_{i=1}^{n}a_i=1$

假设x递增，那么当$a_1$=1时ans最小，所以海拔只有0/1两种取值

---

T4线性代数

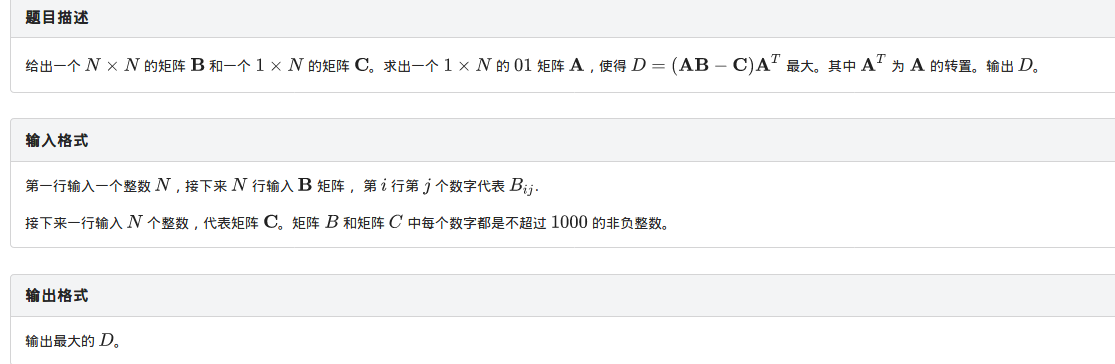
$ans=\sum_{i=1}^{n}\sum_{j=1}^{n}a[i]*a[j]*b[i][j]-\sum_{i=1}^{n}a[i]*c[i]$

考虑建图:(S,i,\sum_{k=1}^{n}b[i][k]),(i,T,c[i]),(i,j,b[i][j]),总收益减去最小割便是答案

这个类型的题我一般都是画出i,j两个点，枚举4种选的情况，

割掉S->i便代表不选，割i->T便代表选

在i，j之间加边来满足真正减去的贡献，就可以建出图来了

可能有些题需要加点，比如一会要讲的T6

---

 

T5人员雇佣

题目描述

作为一个富有经营头脑的富翁，小L决定从本国最优秀的经理中雇佣一些来经营自己的公司。这些经理相互之间合作有一个贡献指数,（我们用Ei,j表示i经理对j经理的了解程度），即当经理i和经理j同时被雇佣时，经理i会对经理j做出贡献，使得所赚得的利润增加Ei,j。当然，雇佣每一个经理都需要花费一定的金钱Ai，对于一些经理可能他做出的贡献不值得他的花费，那么作为一个聪明的人，小L当然不会雇佣他。 然而，那些没有被雇佣的人会被竞争对手所雇佣，这个时候那些人会对你雇佣的经理的工作造成影响，使得所赚得的利润减少Ei,j（注意：这里的Ei,j与上面的Ei,j 是同一个）。 作为一个效率优先的人，小L想雇佣一些人使得净利润最大。你可以帮助小L解决这个问题吗？

输入格式

第一行有一个整数N<=1000表示经理的个数 第二行有N个整数Ai表示雇佣每个经理需要花费的金钱 接下来的N行中一行包含N个数，表示Ei,j，即经理i对经理j的了解程度。（输入满足Ei,j=Ej,i）

输出格式

第一行包含一个整数，即所求出的最大值。

首先明确贡献:

$11:2*e[i][j]$

$10/01:-e[i][j]$

$00:0$

强烈推荐用刚才那个套路，解决此类问题很快的！

建图方法:$(S,i,\sum_{k=1}^{n}e[i][k]),(i,j,2*e[i][j]),(i,T,a[i])$

---

 

T6happiness

题目描述

高一一班的座位表是个n*m的矩阵，经过一个学期的相处，每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了，每个同学对于选择文科与理科有着自己的喜悦值，而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板，想知道如何分配可以使得全班的喜悦值总和最大。

输入格式

第一行两个正整数n，m。
接下来是六个矩阵
第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。
第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。
第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。
第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。
第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。
第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。

输出格式

输出一个整数，表示喜悦值总和的最大值

这道题需要在i,j之间加两个点x,y代表同时选文/理

建图:$(S,i,文),(i,T,理),(S,x,同文),(x,i,INF),(x,j,INF),(i,y,INF),(j,y,INF),(y,T,同理)$

 

---

 

T7千钧一发

题目描述

输入格式

第一行一个正整数N。 第二行共包括N个正整数，第 个正整数表示Ai。 第三行共包括N个正整数，第 个正整数表示Bi。

输出格式

共一行，包括一个正整数，表示在合法的选择条件下，可以获得的能量值总和的最大值。

我们发现偶数和偶数之间不可能矛盾，因为可以满足条件2

奇数和奇数之间也不可能矛盾，因为可以满足条件1,

因为把平方对4取mod，余数是0(偶数)/1(奇数)，

所以对于两个奇数x，y:(x^2+y^2)%4=2，不可能是平方数

所以直接把a[]按奇偶分开，跑最小割即可