网络流模型的性质
1>容量限制:$f(x,y)$<=$c(x,y)$
2>斜对称:$f(x,y)$=-$f(y,x)$
3>流守恒:除了S或者T,每个点的流出流量等于流入流量
最大流
最大流问题是指给定S和T,求出S到T的最大流量
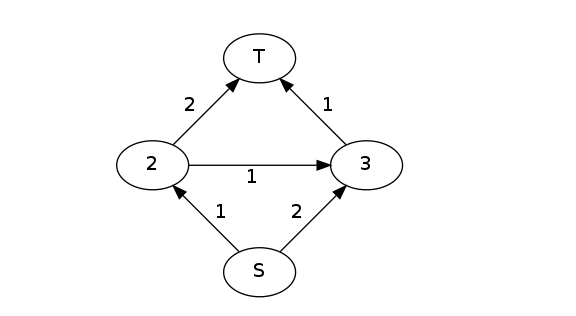
这个图的最大流就是2,但是假如我们把这个图给skyh的话,他一定会走S->2->3->T,流量为1
之后他就写比了
我们如何该用一些反悔的操作来保证最大流呢?
用增广路
我们把skyh的图利用斜对称的性质进行反向边加流后拿出来看一看

神奇的是,我们又发现了一条路径,所以继续流过去

最后达到了与最优解一样的效果
增广路一般会用到Ek或dinic算法
但在最大流中一般用dinic
相同的是都先用对图分层,不同的是dinic是多路增广
代码就不放啦
T1奇怪的游戏
Blinker最近喜欢上一个奇怪的游戏。
这个游戏在一个 N*M 的棋盘上玩,每个格子有一个数。每次 Blinker 会选择两个相邻的格子,并使这两个数都加上 1。
现在 Blinker 想知道最少多少次能使棋盘上的数都变成同一个数,如果永远不能变成同一个数则输出-1。
输入的第一行是一个整数T,表示输入数据有T轮游戏组成。
每轮游戏的第一行有两个整数N和M, 分别代表棋盘的行数和列数。
接下来有N行,每行 M个数。
对于每个游戏输出最少能使游戏结束的次数,如果永远不能变成同一个数则输出-1。
相邻格子不难想到二分图染色,设白色的个数为$sum1$,总和为$num1$,黑色为$sum2$,$num2$,最终状态为x
那么便有$sum1*x-num1$=$sum2*x-num2$
1>$sum1$=$sum2$
直接二分并且用网络流$check$
注意需要满足$num1$=$num2$
2>$sum1$!=$sum2$($abs$($sum1-sum2$)=1)
$x$=$abs$($num1$-$num2$),$check$一下是否合法便是答案
网络流建图:
($S$,$white$,$x-last$),($black$,$T$,$x-last$),($white$,$black$,$INF$)
T2士兵占领
有一个M * N的棋盘,有的格子是障碍。现在你要选择一些格子来放置一些士兵,一个格子里最多可以放置一个士兵,障碍格里不能放置士兵。我们称这些士兵占领了整个棋盘当满足第i行至少放置了Li个士兵, 第j列至少放置了Cj个士兵。现在你的任务是要求使用最少个数的士兵来占领整个棋盘。
第一行两个数M, N, K分别表示棋盘的行数,列数以及障碍的个数。
第二行有M个数表示Li。 第三行有N个数表示Ci。
接下来有K行,每行两个数X, Y表示(X, Y)这个格子是障碍。
输出一个数表示最少需要使用的士兵个数。如果无论放置多少个士兵都没有办法占领整个棋盘,输出”JIONG!” (不含引号)
考虑把至少放置转化成至多不放置,之后按行列转化成二分图,可以放置的地方化为边
于是它便成了一道最大流板子题
T3紧急疏散
发生了火警,所有人员需要紧急疏散!假设每个房间是一个N M的矩形区域。每个格子如果是'.',那么表示这是一块空地;如果是'X',那么表示这是一面墙,如果是'D',那么表示这是一扇门,人们可以从这儿撤出房间。已知门一定在房间的边界上,并且边界上不会有空地。最初,每块空地上都有一个人,在疏散的时候,每一秒钟每个人都可以向上下左右四个方向移动一格,当然他也可以站着不动。疏散开始后,每块空地上就没有人数限制了(也就是说每块空地可以同时站无数个人)。但是,由于门很窄,每一秒钟只能有一个人移动到门的位置,一旦移动到门的位置,就表示他已经安全撤离了。现在的问题是:如果希望所有的人安全撤离,最短需要多少时间?或者告知根本不可能。
第一行是由空格隔开的一对正整数N与M,3<=N <=20,3<=M<=20,
以下N行M列描述一个N M的矩阵。其中的元素可为字符'.'、'X'和'D',且字符间无空格。
只有一个整数K,表示让所有人安全撤离的最短时间,
如果不可能撤离,那么输出'impossible'(不包括引号)。
这道题用到了一个常用的套路:按时间拆点
显然满足单调性,但是直接二分会T,
我们发现check复杂度过高,反而二分的区间很小
所以考虑直接枚举时间,在上一个时间的残余网络上跑最大流





