2019.11.12&13题解

写在前面:

虽然拿到了rk1，但是T3被卡常TLE90分，(考后再交就A了!?)，lemon80，又丢失了一次良好的AK机会，

掐头去尾距离联赛仅剩2天，最近中午一直睡不好，可能是有些紧张，

希望自己接下来几天能放平心态，从吾心，尽吾力就好。

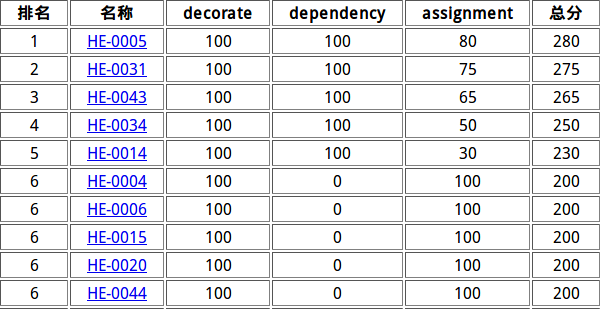
A. 装饰

标签：

规律

题解：

假设a为最大值

1>a<=2*(b+c) ans=(a+b+c)/3

这种情况下不会出现a 0 0的情况，答案就是(a+b+c)/3

2>otherwise ans=b+c

反之，最多b+c次之后就会用完b,c,所以ans=b+c

B. 循环依赖

标签：

读入+Top

题解：

这题能读进来就是个Top模板题，然而有许多dalao因读入挂了100分

 

C. 任务分配

标签：

最短路+Dp

题解：

首先求去正反最短路之后设a[i]=dis[0][i]+dis[1][i]，则考虑把a从小到大排序，则有以下性质：

性质1:子项目对应的点一定连续

性质2:子项目分出的区间一定单调不增

Day2

写在前面：

比赛结束后波波老师打开result...

啊？这是今天的榜吗，怎么又rk1了，T2不是伪了吗，怎么AC了？

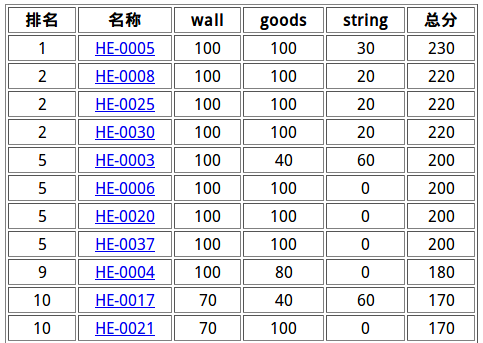
A. ZYB建围墙

标签：

规律

题解：

我在考场上找到了一个不能证明的规律:新加一个点的代价是(3-它周围的点的个数)

所以点越集中越好，考虑二分完整6边形的长度k，之后把剩余的加在其周围，

剩余的第一个需要外加1，并且代价是1,0,0,0,1,0,0,0...循环节为k+1

所以便有：ans=6*(k+1)+(m!=0)+m/(k+1)

B. ZYB和售货机

标签：

基环内向树

题解：

首先可以把所以的i全部用最优非负转移点(设为g[i])转移a[i]-1次,之后考虑把i向g[i]建边

发现建出的图是基环树森林，首先用Top把树的枝叶全部撸掉，贡献直接加上与原先一样，

之后枚举环上的点，找出最小断环代价即可

考场上我觉得树之间的最小断环代价可能会出环，但是我忽略了一个优美的性质，

每个点的入度出度都不可能超过1，所以次大转移点不可能是另一棵树的环，这样转移就不会出环

C. ZYB玩字符串

标签：

区间Dp

题解：

这道题的Dp定义挺新颖的：

设f[i][j]代表[i,j]是否可以被消成p的前缀(可以为空)，这样转移的复杂度将会大大降低

考虑j的身份转移：

1>j与前面的零碎构成p的前缀：f[i][j]|=f[i][j-1]&(s[j]==s[i+(j-i)%len+1])

2>j是整块的:f[i][j]|=f[i][j-k*len]&f[j-k*len+1][j]

加几个DeepinC所讲的剪枝：len能否整除n，map记忆化，[L,R]26个字母个数是不是分别整除[1,n]26个字母的个数...就可以通过本题