2019.07.07考试报告

T1[SDOI2015] 排序

考试思路

很真实的一道dfs题。

考场上推了推规律，连了连边什么的，发现还是dfs比较好，

所以直接dfs。期望得分20，实际30

正解

首先我们可以发现一个操作序列的全排列都是合法的。

所以我们可以操作从小到大进行，比如说到了第i个：

设交换长度为l。那么就把序列分成l*2的若干块之后判断是否严格递增（注意必须是a[j]=a[j-1]+1）为什么要这么做？因为这次i用完之后便无法改变l*2的序列里的大小关系了，设检查出来不符合的有tot个，所以便有以下几种情况：

First：tot>2 显然怎么换都不行

Second：tot=1 这个块内部交换

Third： tot=2 （1 2 3 4）13 14 23 24四种操作

Fourth：tot=0 跳过这一个操作

（以上每个交换后都去check一下是否严格递增）

 

 

T2 [APIO2016] 划艇

考试思路

简单的推了一下dp式子，但很不幸的是样例太水竟然过了。

期望得分31分 实际得分0分。

早知道就直接去搞a==b的9分了，可以从rank4水到rank3。

正解

很好的一道dp题啊，第一次做到离散化区间的dp。

我们把a和b+1都离散成左开右闭的区间，这样便可以dp了

设f[i][j]为i必须取且取的数在离散化后的第j个区间。

我们枚举最后一个不去第j区间的学校k，那么便有：

 

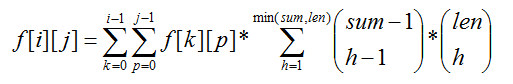
其中sum为[k+1,i]中可以取到j区间的学校个数

化简一下就是

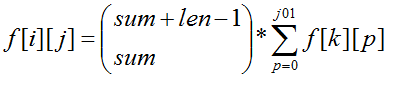
用前缀和以及递推组合数便可以把复杂度化成O（n^3）

 

 

T3 [CQOI2011] 放棋子

考试思路

 依然是dfs。。。

正解

https://www.cnblogs.com/BCOI/p/10491544.html