[牛客21295]奇异图(构造+贪心+Flyod)

题目链接：

https://ac.nowcoder.com/acm/problem/21295?&headNav=acm

题目描述

有一张n个点的无向完全图，给每一条边规定一个方向后可以得到一个新图
我们称这样的图为奇异图
现在只知道奇异图每个点的出度
你需要计算有多少点对(u, v) u可以到达v，特殊的，每个点自己都可以到达自己
保证答案唯一

输入描述:

第一行输入一个整数n (1 ≤ n ≤ 100)
第二行输入n个整数a[i]

输出描述:

输出一个整数

---

 

题解：

%%%skyh图论小皇子

%%%B哥图论太上皇

首先看到这道题一定会想到不会是计数，那就是图论，又因为数据保证答案唯一，所以大概可以猜出是建图跑最短路

建图很神：每次找出当前出度最小的点，把其入度与以后的出度大的点挨个匹配，出度同理，这样便可以防止出现下面的情况：

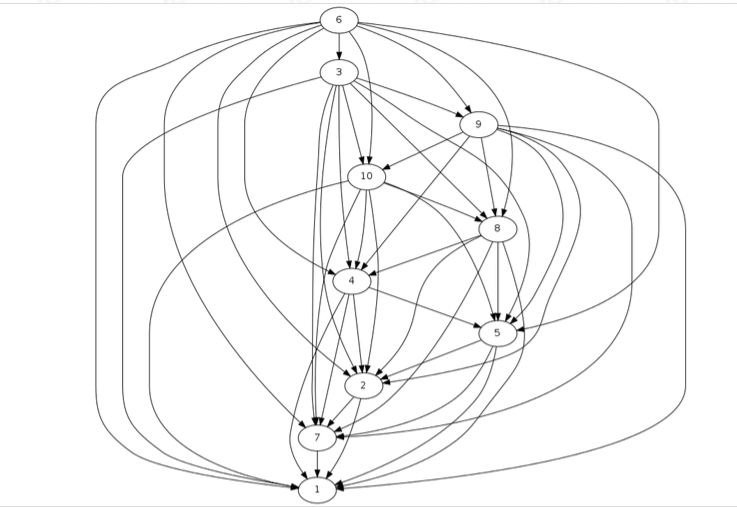
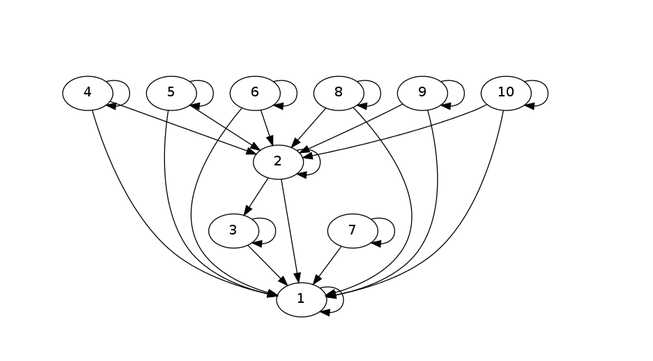
错解是直接找能建边就建边，但是3这个点本应该是->2，但是它在2的时候被2改变了方向变成了2->3，这导致了2无法满足入度需求，

反观正解的思路:用最大的出度向当前点连边，便可以解决这种情况:它最大可能的保留了可以连出/入的点的个数，以便后面成功建图

所以其正确性是可以证明的。

---

 

最后附上代码:

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int ans,n,e[105][105];
struct node{int id,in,out;}a[105];
bool comp1(node l,node r){return l.out<r.out;}
bool comp2(node l,node r){return l.in>r.in;}
signed main()
{
        //freopen("1.in","r",stdin);
        scanf("%d",&n);
        for(int i=1;i<=n;i++) a[i].id=i,e[i][i]=1,scanf("%d",&a[i].out),a[i].in=n-a[i].out-1;
        for(int i=1;i<n;i++)
        {
                sort(a+i,a+n+1,comp2);
                for(int j=i+1;j<=n;j++)
                {
                        if(!a[i].out) break;
                        a[i].out--,a[j].in--;
                        e[a[i].id][a[j].id]=1;
                }
                sort(a+i,a+n+1,comp1);
                for(int j=n;j>=i+1;j--)
                {
                        if(!a[i].in) break;
                        if(e[a[i].id][a[j].id]) continue;
                        a[i].in--,a[j].out--;
                        e[a[j].id][a[i].id]=1;
                }
        }
        for(int k=1;k<=n;k++)
        {
                for(int i=1;i<=n;i++)
                {
                        for(int j=1;j<=n;j++)
                        {
                                e[i][j]|=e[i][k]&e[k][j];
                        }
                }
        }
        for(int i=1;i<=n;i++)
        {
                for(int j=1;j<=n;j++)
                {
                        ans+=e[i][j];
                }
        }
        printf("%d",ans);
        return 0;
}