[BZOJ4358] permu
题目大意：给出一个长度为n的排列P(P1,P2,...Pn)，以及m个询问。每次询问某个区间[l,r]中，最长的值域 连续段长度。
好题啊，卡了我两天的好题...
刚开始打的是线段树+莫队，成功TLE（难调得一批我就弃掉了）。
之后颓了一波题解发现自己思路是对的但需要卡常（我可不擅长这东西...）
果断转正解回滚莫队+并查集。
首先我们可以按（b[l],r）二元组进行排序，我们便会得到一块一块左端点所在区间相同且右端点递增的块（最多根号n块），
之后我们每次都暴力枚举左端点更新答案之后清空，这样莫队便滚起来了。
这个题打并查集真的很考察细节，我在这里把坑们一个一个列了出来
坑点一：并查集要用两个。这个不用多说因为用一个的话无法回滚。
坑点二：回滚的并差集要记录左右最远值域，而不能用size代替，但原并查集就可以。
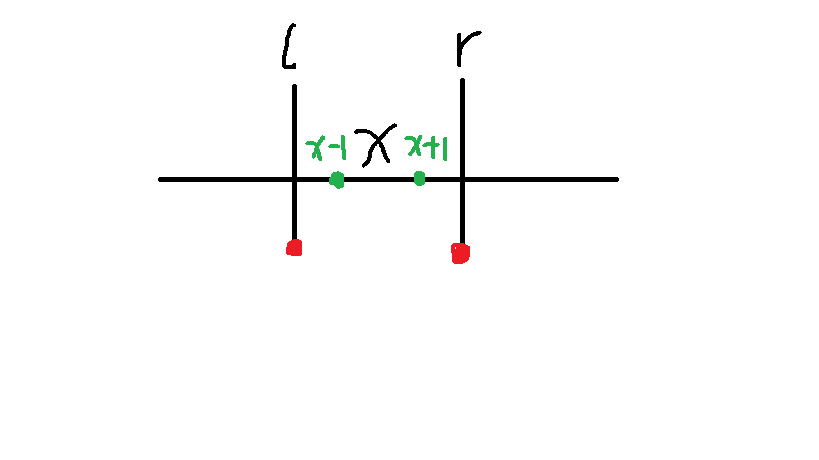
如图所示，我们如果只把x-1和x+1的祖先（假设就是他们）的暂时父亲指向x，那么下一次若是添加红点旁边的便是查询红点便只能在原并查集里查到，
但查不到刚刚标记的size[x]了，所以我们要记录左右最远值域来保证以后的更新是正确的。
坑点三：对于那些l，r在同一块内的询问我们可以暴力做，复杂度根号n。
坑点四：每次左端点换块时都要清空原并查集供下次使用，并且把莫队的端点设为所在块的右端点。由于我们每次都是O（n）的复杂度总共搞根号n次，所以总复杂度很优秀。
坑点五：清空暂时并查集时要注意复杂度，可以用一个栈来实现。代码片段如下：
if(mn[x]!=x)
{
st[++top]=mn[x];
Fa[mn[x]]=x;
}
if(mx[x]!=x)
{
st[++top]=mx[x];
Fa[mx[x]]=x;
}
while(top)
{
int x=st[top--];
Fa[x]=0;
}
坑点六：并查集的压缩路径会破坏原有的父子关系，我们要另开并查集维护。
代码如下：
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#define AA cout<<"Alita"<<endl
using namespace std;
const int N=5e4+100;
int top,sum,cnt,L,R,k,n,m,size[N],ans[N],p[N],b[N],fa[N],Fa[N],st[N],mn[N],mx[N];
struct question{int l,r,id;}q[N];
bool comp(question x,question y)
{
if(b[x.l]==b[y.l]) return x.r<y.r;
return b[x.l]<b[y.l];
}
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
int Find(int x)
{
if(x==Fa[x]) return x;
return Fa[x]=Find(Fa[x]);
}
void add1(int x)
{
int z;
fa[x]=x;
size[x]=1;
if(z=find(x-1))
{
fa[z]=x;
size[x]+=size[z];
}
if(z=find(x+1))
{
fa[z]=x;
size[x]+=size[z];
}
sum=max(sum,size[x]);
}
void add2(int x)
{
int z;
st[++top]=x;
Fa[x]=x;
mn[x]=mx[x]=x;
if(z=Find(x-1)) mn[x]=mn[z];
else if(z=find(x-1)) mn[x]-=size[z];
if(z=Find(x+1)) mx[x]=mx[z];
else if(z=find(x+1)) mx[x]+=size[z];
if(mn[x]!=x)
{
st[++top]=mn[x];
Fa[mn[x]]=x;
}
if(mx[x]!=x)
{
st[++top]=mx[x];
Fa[mx[x]]=x;
}
sum=max(sum,mx[x]-mn[x]+1);
}
int main()
{
//freopen("3.in","r",stdin);
//freopen("D.out","w",stdout);
scanf("%d%d",&n,&m);
k=sqrt(n);
for(int i=1;i<=n;i++)
{
scanf("%d",&p[i]);
b[i]=(i-1)/k+1;
}
for(int i=1;i<=m;i++)
{
q[++cnt].id=i;
scanf("%d%d",&q[cnt].l,&q[cnt].r);
if(b[q[cnt].l]==b[q[cnt].r])
{
sum=0;
for(int j=q[cnt].l;j<=q[cnt].r;j++) add2(p[j]);
ans[i]=sum;
while(top)
{
int x=st[top--];
Fa[x]=0;
}
cnt--;
}
}
stable_sort(q+1,q+cnt+1,comp);
for(int i=1;i<=cnt;i++)
{
if(b[q[i].l]!=b[q[i-1].l])
{
sum=0;
for(int j=1;j<=n;j++) //最多根号n次
{
fa[p[j]]=Fa[p[j]]=size[p[j]]=0;
}
L=R=min(n,b[q[i].l]*k);
}
while(R<q[i].r) add1(p[++R]);
int tmp=sum;
for(int j=q[i].l;j<=L;j++) add2(p[j]);
ans[q[i].id]=sum;
sum=tmp;
while(top)
{
int x=st[top--];
Fa[x]=0;
}
}
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
这个题我竟然写了这么长，122行
