[BZOJ1227] 虔诚的墓主人 (线段树+组合计数)

这是一道出现在数学专题里的数据结构题（波波真棒啊~）

式子很好写：

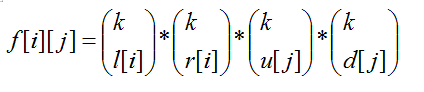
但是我们发现n,m<=1e9,所以应该在常青树上做文章

先把它们离散化这不用说

之后我们可以一列一列的扫，用线段树区间查询每两课常青树中的C(l[i],k)*C(r[i],k)值

之后*=C(u[j],k)*C(d[j],k)即可(它们的u和d都是一样的)

最后单点更新一下这棵树所在的行的C(l[i],k)*C(r[i],k)。

因为模数非素，且k<=10所以组合数要用杨辉三角打表。

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<map>
#include<cmath>
using namespace std;
const int N=1e5+10;
const int mod=2147483648;
int k,tot,cnt,ans,n,m,w,U[N],D[N],L[N],R[N],C[N][15];
map<int,int>mx,my;
struct Taylor{int x,y,X,Y;}b[N];
struct Swift{int l,r,w;}a[N*4];
bool comp2(Taylor l,Taylor r)
{
        return l.Y<r.Y;
}
bool comp1(Taylor l,Taylor r)
{
        if(l.X==r.X) return l.Y<r.Y;
        return l.X<r.X;
}
void build(int k,int l,int r)
{
        a[k].l=l;
        a[k].r=r;
        if(l==r) return;
        int mid=(l+r)>>1;
        build(k<<1,l,mid);
        build(k<<1|1,mid+1,r);
}
void change(int k,int x,int y)
{
        if(a[k].l==a[k].r)
        {
                a[k].w=y;
                return;
        }
        int mid=(a[k].l+a[k].r)>>1;
        if(x<=mid) change(k<<1,x,y);
        else change(k<<1|1,x,y);
        a[k].w=a[k<<1].w+a[k<<1|1].w;
}
int query(int k,int l,int r)
{
        if(a[k].l>=l&&a[k].r<=r) return a[k].w;
        int mid=(a[k].l+a[k].r)>>1,sum=0;
        if(l<=mid) sum+=query(k<<1,l,r);
        if(r>mid) sum+=query(k<<1|1,l,r);
        return sum;
}
void init()
{
        stable_sort(b+1,b+w+1,comp2);
        for(int i=1;i<=w;i++)
        {
                if(my[b[i].Y]==0) my[b[i].Y]=++cnt;
                b[i].y=my[b[i].Y];
                R[b[i].y]++;
        }
        stable_sort(b+1,b+w+1,comp1);
        for(int i=1;i<=w;i++)
        {
                if(mx[b[i].X]==0) mx[b[i].X]=++tot;
                b[i].x=mx[b[i].X];
        }
        C[0][0]=1;
        for(int i=1;i<=w;i++)
        {
                C[i][0]=1;
                for(int j=1;j<=min(k,i);j++)
                {
                        C[i][j]=C[i-1][j]+C[i-1][j-1];
                }
        }
        for(int i=1;i<=w;i++)
        {
                if(b[i].x!=b[i-1].x) continue;
                D[i]=D[i-1]+1;
        }
        for(int i=w;i>=1;i--)
        {
                if(b[i].x!=b[i+1].x) continue;
                U[i]=U[i+1]+1;
        }
        build(1,1,cnt);
}
int main()
{
        //freopen("1.in","r",stdin);
        scanf("%d%d%d",&n,&m,&w);
        for(int i=1;i<=w;i++)
        {
                scanf("%d%d",&b[i].X,&b[i].Y);
        }
        scanf("%d",&k);
        init();
        for(int i=1;i<=w;i++)
        {
                R[b[i].y]--;
                L[b[i].y]++;
                change(1,b[i].y,C[L[b[i].y]][k]*C[R[b[i].y]][k]);
                if(b[i].x!=b[i-1].x||b[i].y==b[i-1].y+1) continue;
                ans+=query(1,b[i-1].y+1,b[i].y-1)*C[U[i]+1][k]*C[D[i]][k];
        }
        printf("%d",ans&(mod-1));
        return 0;
}