[BZOJ] 2142 礼物 (exLucas+中国剩余定理)

一句话题意：给定n,m,p;求

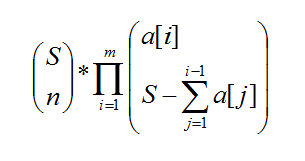
（p通过唯一分解后pi^ci<=1e5）

p不为素数，所以得用到exLucas（我也是今天现学的T_T）

p=p1^c1*p2^c2*......pk^ck

只要求出ans%pi^ci便可以列出来k个关于ans的同余式子，用中国剩余定理求出解即可。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
const int N=1e5+10;
ll cnt,S,P,n,m,a[7],p[N],b[N],c[N];
ll poww(ll x,ll y,ll p)
{
        ll sum=1;
        while(y)
        {
                if(y&1) sum=(sum*x)%p;
                y>>=1;
                x=(x*x)%p;
        }
        return sum;
}
ll fac(ll n,ll p,ll pk)
{
        if(!n) return 1;
        ll sum=1;
        for(ll i=1;i<pk;i++)
        {
                if(i%p)
                {
                        sum=(sum*i)%pk;
                }
        }
        sum=poww(sum,n/pk,pk);
        for(ll i=1;i<=n%pk;i++)
        {
                if(i%p)
                {
                        sum=(sum*i)%pk;
                }
        }
        return sum*fac(n/p,p,pk)%pk;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
        if(!b)
        {
                x=1;
                y=0;
                return a;
        }
        ll gcd=exgcd(b,a%b,x,y);
        ll t=x;
        x=y;
        y=t-a/b*y;
        return gcd;
}
ll inv(ll h,ll p)
{
        ll x,y;
        exgcd(h,p,x,y);
        return (x%p+p)%p;
}
ll C(ll n,ll m,ll p,ll pk)
{
        if(n<m) return 0;
        ll tot=0;
        ll f1,f2,f3;
        f1=fac(n,p,pk);
        f2=fac(m,p,pk);
        f3=fac(n-m,p,pk);
        for(ll i=n;i;i/=p) tot+=i/p;
        for(ll i=m;i;i/=p) tot-=i/p;
        for(ll i=n-m;i;i/=p) tot-=i/p;
        return f1*inv(f2,pk)%pk*inv(f3,pk)%pk*poww(p,tot,pk)%pk;
}
bool check(ll x)
{
        for(int i=2;i<=sqrt(x);i++)
        {
                if(x%i==0) return true;
        }
        return false;
}
void init(ll g)
{
        for(int i=2;i<=g;i++)
        {
                if(g%i) continue;
                if(check(i)) continue;
                p[++cnt]=i;
                b[cnt]=i;
                g/=i;
                while(g%i==0)
                {
                        b[cnt]*=i;
                        g/=i;
                }
        }
}
void get(int x)
{
        ll v=0;
        c[x]=C(n,S,p[x],b[x]);
        for(int i=1;i<=m;i++)
        {
                c[x]=(c[x]*C(S-v,a[i],p[x],b[x]))%b[x];
                v+=a[i];
        }
}
void China()
{
        ll ans=0;
        for(int i=1;i<=cnt;i++)
        {
                ll l=P/b[i],r=b[i],x,y;
                exgcd(l,r,x,y);
                (ans+=l*x*c[i]%P)%=P;
                ans=(ans%P+P)%P;
        }
        printf("%lld",ans);
}
int main()
{
        //freopen("1.in","r",stdin);
        scanf("%lld%lld%lld",&P,&n,&m);
        for(int i=1;i<=m;i++)
        {
                scanf("%lld",&a[i]);
                S+=a[i];
        }
        if(n<S)
        {
                puts("Impossible");
                return 0;
        }
        init(P);
        for(int i=1;i<=cnt;i++) get(i);
        China();
        return 0;
}