[BZOJ2839] 集合计数 (容斥+组合)

题目描述

一个有N个元素的集合有2^N个不同子集（包含空集），现在要在这2^N个集合中取出若干集合（至少一个），使得它们的交集的元素个数为K，求取法的方案数，答案模1e9+7。

 

 

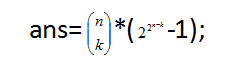
上式对吗？显然是不对的，以为它不仅统计了交集为k的而且统计了交集为k以上的。

所以我们要用容斥。

设g[i]为交集大于等于i的方案数，

那么:

　　

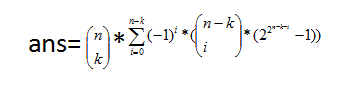
用文字解释就是“任意取-g[1]+g[2]-g[3]...”;

注意一下的指数在处理的时候要%(mod-1)而不是mod(欧拉定理的推论)。

阶乘和逆元预处理即可。

 

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int N=1e6+5,mod=1e9+7;
ll ans,n,k,fac[N],inv[N];
ll poww(ll x,ll y,ll z)
{
        ll sum=1;
        while(y)
        {
                if(y&1) sum=(sum*x)%z;
                y>>=1;
                x=(x*x)%z;
        }
        return sum;
}
ll C(ll x,ll y)
{
        return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int main()
{
        //freopen("1.in","r",stdin);
        //freopen("2.out","w",stdout);
        scanf("%lld%lld",&n,&k);
        fac[0]=1;
        for(ll i=1;i<=n;i++)
        {
                fac[i]=fac[i-1]*i%mod;
        }
        inv[n]=poww(fac[n],mod-2,mod);
        for(ll i=n-1;i>=0;i--)
        {
                inv[i]=inv[i+1]*(i+1)%mod;
        }
        for(ll i=n-k;i>=0;i--)
        {
                ll S=poww(2,n-k-i,mod-1);
                S=poww(2,S,mod);
                (ans+=((i&1)==1?-1:1)*C(n-k,i)*(S-1)%mod)%=mod;
                ans=(ans+mod)%mod;
        }
        (ans*=C(n,k))%=mod;
        printf("%lld",ans);
        return 0;
}