2024 jscpc B题 Area of the Devil 题解

合集 - xcpc题解集1(4)

1.2024 jscpc B题 Area of the Devil 题解2024-05-16

2.2024 jscpc E题 Divide题解2024-05-143."华为智联杯"无线程序设计大赛 B题 异或和之和题解2024-06-194.[SNCPC2024] 2024 年陕西省大学生程序设计 J题猜质数II 题解2024-07-06

收起

题目链接：Area of the Devil

算不在题目说的区域内的面积，直接算是比较麻烦的，这里给一个朋友直接算画的图，其实画出区域以后也算好算，当然官解提到的容斥去算更好写。

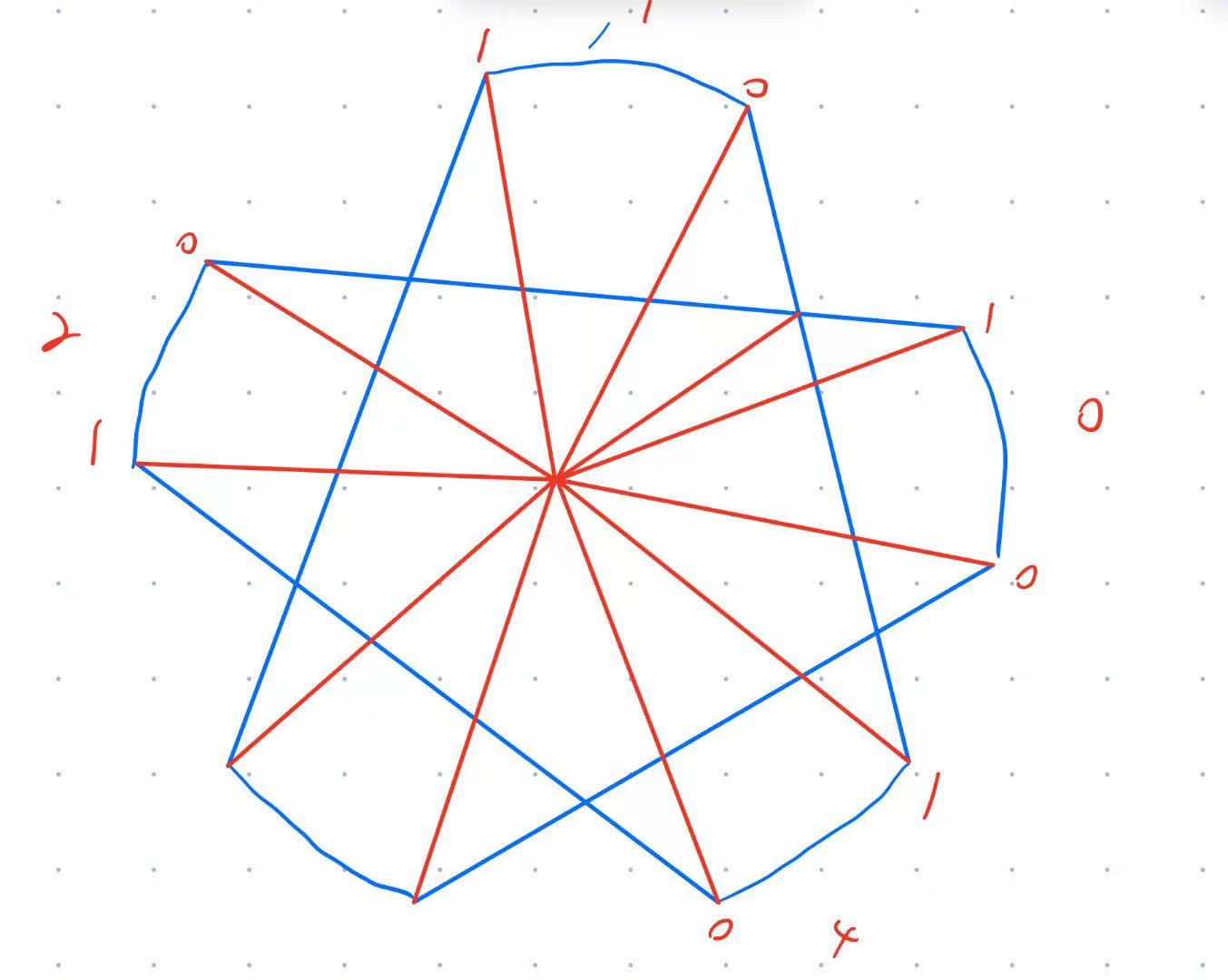
一共有五个空余的区域，我们考虑这五个区域怎么计算，图一是直接画出的所有区域的并集，图二则是五角星处于边界情况时，图上的三角形+弓形 即为某一块的未入并集区域，即非魔鬼区域。算出交点以后，就是最基本的初高中数学问题了，三角形面积可以用矢量来算，弓形面积的话，初中问题，圆心固定的，然后改为算对应的扇形-三角形即可，由于题目给出了夹角度数，所以可以考虑直接使用正弦定理算面积。稍微注意下边界怎么取的，结合图一图二，我们发现，从左往右依次数四个点，前两个取圆弧起点，另外两个取圆弧终点，然后交叉匹配就是组成的区域和直线了。尽量用矢量做计算，如果算出直线方程，可能直线斜率不存在，所以尽量用矢量计算交点。

参照代码

#include <bits/stdc++.h>
 
// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
 
// #define isPbdsFile
 
#ifdef isPbdsFile
 
#include <bits/extc++.h>
 
#else
 
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
 
#endif
 
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
 
template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}
 
template <typename T>
T lowBit(T x)
{
    return x & -x;
}
 
template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}
 
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}
 
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c) if (b & 1) (ans *= a) %= c;
    return modt(ans, c);
}
 
template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-') sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}
 
template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}
 
template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char)) return;
    if (x < 0) x = -x, putchar('-');
    if (x > 9) write(x / 10);
    putchar(x % 10 ^ 48);
}
 
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}
 
 
template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;
 
    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow) return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }
 
    T3()
    {
        one = tow = three = 0;
    }
 
    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};
 
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y) x = y;
}
 
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y) x = y;
}
 
namespace Geometry2D
{
    //精度
    constexpr ld EXP = 1e-12;
    //Π
    const ld PI = acos(-1.0);
 
    ld sign(const ld x)
    {
        if (!fabs(x)) return 0;
        return x / fabs(x);
    }
 
    struct Point
    {
        ld x, y;
 
        Point() = default;
 
        Point(const ld x, const ld y) : x(x), y(y)
        {
        };
 
        Point operator+(const Point other) const
        {
            return Point(x + other.x, y + other.y);
        }
 
        Point operator-(const Point other) const
        {
            return Point(x - other.x, y - other.y);
        }
 
        Point operator*(const ld k) const
        {
            return Point(x * k, y * k);
        }
 
        Point operator/(const ld k) const
        {
            return Point(x / k, y / k);
        }
 
        bool operator==(const Point other) const
        {
            return fabs(x - other.x) < EXP && fabs(y - other.y) < EXP;
        }
 
        bool operator<(const Point other) const
        {
            return x != other.x ? x < other.x : y < other.y;
        }
    };
 
    //两点距离
    inline ld Distance(const Point x, const Point y)
    {
        return hypot(x.x - y.x, x.y - y.y);
    }
 
    typedef Point Vector;
 
    //点乘
    inline ld Dot(const Vector A, const Vector B)
    {
        return A.x * B.x + A.y * B.y;
    }
 
    //模长
    inline ld Len(const Vector A)
    {
        return sqrt(Dot(A, A));
    }
 
    //模长平方
    inline ld Len2(const Vector A)
    {
        return Dot(A, A);
    }
 
    //两向量夹角度数
    inline ld Angle(const Vector A, const Vector B)
    {
        return acos(Dot(A, B) / Len(A) / Len(B));
    }
 
    //叉乘
    inline ld Cross(const Vector A, const Vector B)
    {
        return A.x * B.y - A.y * B.x;
    }
 
    //三点构成的平行四边形面积
    inline ld Area2(const Point A, const Point B, const Point C)
    {
        return Cross(B - A, C - A);
    }
 
    //逆时针旋转度数
    inline Vector Rotate(const Vector A, const ld rad)
    {
        return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * cos(rad) + A.y * sin(rad));
    }
 
    //法向量的单位向量
    inline Vector Normal(const Vector A)
    {
        return Vector(-A.y / Len(A), A.x / Len(A));
    }
 
    //叉乘检验两向量是否重合
    inline bool Parallel(const Vector A, const Vector B)
    {
        return fabs(Cross(A, B)) < EXP;
    }
 
    struct Line
    {
        Point p1, p2;
 
        Line() = default;
 
        //两点式
        Line(const Point& p1, const Point& p2) : p1(p1), p2(p2)
        {
        }
 
        //点斜式
        Line(const Point& p, const ld angle)
        {
            p1 = p, p2 = p1 + (fabs(angle - PI / 2) < EXP ? Point(0, 1) : Point(1, tan(angle)));
        }
 
        //一般式
        Line(const ld a, const ld b, const ld c)
        {
            if (fabs(a) < EXP) p1 = Point(0, -c / b), p2 = Point(1, -c / b);
            else if (fabs(b) < EXP) p2 = Point(-c / a, 0), p2 = Point(-c / a, 1);
            else p1 = Point(0, -c / b), p2 = Point(1, (-c - a) / b);
        }
    };
 
    typedef Line Segment;
 
    //点和直线的关系
    inline int Point_line_relation(const Point p, const Line& v)
    {
        int c = Cross(p - v.p1, v.p2 - v.p1);
        if (c < 0) return 1; //p在v的左侧
        if (c > 0) return 2; //p在v的右侧
        return 0; //p在v上
    }
 
    //点是否在线段上
    inline bool Point_on_seg(const Point p, const Segment& v)
    {
        return fabs(Cross(p - v.p1, v.p2 - v.p1)) < EXP && Dot(p - v.p1, p - v.p2) <= 0;
    }
 
    //点到直线的距离
    inline ld Dis_point_line(const Point p, const Line& v)
    {
        return fabs(Cross(p - v.p1, v.p2 - v.p1)) / Distance(v.p1, v.p2);
    }
 
    //点在直线上的投影
    inline Point Point_line_proj(const Point p, const Line& v)
    {
        ld k = Dot(v.p2 - v.p1, p - v.p1) / Len2(v.p2 - v.p1);
        return v.p1 + (v.p2 - v.p1) * k;
    }
 
    //点关于直线的对称点
    inline Point Point_line_symmetry(const Point p, const Line& v)
    {
        Point q = Point_line_proj(p, v);
        return Point(2 * q.x - p.x, 2 * q.y - p.y);
    }
 
    //点到线段的距离
    inline ld Dis_point_seg(const Point p, const Segment& v)
    {
        if (Dot(p - v.p1, v.p2 - v.p1) < 0 || Dot(p - v.p2, v.p1 - v.p2) < 0)
            return min(
                Distance(p, v.p1), Distance(p, v.p2));
        return Dis_point_line(p, v);
    }
 
    //两直线的位置关系
    inline int Line_relation(const Line& v1, const Line& v2)
    {
        if (Cross(v1.p2 - v1.p1, v2.p2 - v2.p1) < EXP)
        {
            if (fabs(Point_line_relation(v1.p1, v2)) < EXP) return 1; //重合
            return 0; //平行
        }
        return 2; //相交
    }
 
    //两直线交点
    inline Point Cross_point(const Point a, const Point b, const Point c, const Point d)
    {
        ld s1 = Cross(b - a, c - a);
        ld s2 = Cross(b - a, d - a);
        return Point(c.x * s2 - d.x * s1, c.y * s2 - d.y * s1) / (s2 - s1);
    }
 
    //两条线段是否相交
    inline bool Cross_segment(const Point a, const Point b, const Point c, const Point d)
    {
        ld c1 = Cross(b - a, c - a), c2 = Cross(b - a, d - a);
        ld d1 = Cross(d - c, a - c), d2 = Cross(d - c, b - c);
        return sign(c1) * sign(c2) < 0 && sign(d1) * sign(d2) < 0; //1相交 0不相交
    }
 
    //点和多边形的关系
    inline int Point_in_polygon(const Point pt, const Point* p, const int n)
    {
        forn(i, 0, n - 1) if (p[i] == pt) return 3; //在多边形的顶点上
        forn(i, 0, n - 1)
        {
            Line v = Line(p[i], p[(i + 1) % n]);
            if (Point_on_seg(pt, v)) return 2; //在多边形上
        }
        int num = 0;
        forn(i, 0, n - 1)
        {
            int j = (i + 1) % n;
            int c = sign(Cross(pt - p[i], p[i] - p[j]));
            int u = sign(p[i].y - pt.y);
            int v = sign(p[j].y - pt.y);
            if (c > 0 && u < 0 && v >= 0) num++;
            if (c < 0 && u >= 0 && v < 0) num--;
        }
        return num != 0;
    }
 
    //多边形面积
    inline ld Polygon_area(const Point* p, const int n)
    {
        ld area = 0;
        forn(i, 0, n - 1) area += Cross(p[i], p[(i + 1) % n]);
        return area / 2;
    }
 
    //多边形重心
    inline Point Polygon_center(const Point* p, const int n)
    {
        Point ans(0, 0);
        if (!Polygon_area(p, n)) return ans;
        forn(i, 0, n - 1) ans = ans + (p[i] + p[(i + 1) % n]) * Cross(p[i], p[(i + 1) % n]);
        return ans / Polygon_area(p, n) / 6;
    }
 
    //求凸包,返回顶点,ans为凸包的顶点
    inline int Convex_hull(Point* p, int n, Point* ans)
    {
        n = unique(p, p + n) - p;
        sort(p, p + n);
        int v = 0;
        //下凸包
        forn(i, 0, n - 1)
        {
            while (v > 1 && sign(Cross(ans[v - 1] - ans[v - 2], p[i] - ans[v - 1])) <= 0) v--;
            ans[v++] = p[i];
        }
        int j = v;
        //求上凸包
        forv(i, n - 2, 0)
        {
            while (v > j && sign(Cross(ans[v - 1] - ans[v - 2], p[i] - ans[v - 1])) <= 0) v--;
            ans[v++] = p[i];
        }
        if (n > 1) v--;
        return v;
    }
 
    struct Circle
    {
        Point c; //圆心
        ld r; //半径
        Circle() = default;
 
        Circle(const Point c, const ld r) : c(c), r(r)
        {
        }
 
        Circle(const ld x, const ld y, const ld _r)
        {
            c = Point(x, y), r = _r;
        }
    };
 
    //点到圆的关系
    inline int Point_circle_relation(const Point p, const Circle& c)
    {
        ld dst = Distance(p, c.c);
        if (sign(dst - c.r) < 0) return 0; //圆内
        if (sign(dst - c.r) == 0) return 1; //圆上
        return 2; //圆外
    }
 
    //直线和圆的关系
    inline int Line_circle_relation(const Line& v, const Circle& c)
    {
        ld dst = Dis_point_line(c.c, v);
        if (sign(dst - c.r) < 0) return 0; //圆内
        if (sign(dst - c.r) == 0) return 1; //圆上
        return 2; //圆外
    }
 
    //线段和圆的关系
    inline int Seg_circle_relation(const Segment& v, const Circle& c)
    {
        ld dst = Dis_point_seg(c.c, v);
        if (sign(dst - c.r) < 0) return 0; //圆内
        if (sign(dst - c.r) == 0) return 1; //圆上
        return 2; //圆外
    }
 
    //直线和圆的焦点.pa、pb是交点.返回值是交点的个数
    inline int Line_cross_circle(const Line& v, const Circle& C, Point& pa, Point& pb)
    {
        if (Line_circle_relation(v, C) == 2) return 0; //无交点
        Point q = Point_line_proj(C.c, v); //圆心在直线上的投影点
        double d = Dis_point_line(C.c, v); //圆心到直线距离
        double k = sqrt(C.r * C.r - d * d);
        if (sign(k) == 0)
        {
            //一个交点
            pa = q;
            pb = q;
            return 1;
        }
        Point n = (v.p2 - v.p1) / Len(v.p2 - v.p1); //单位向量
        pa = q + n * k;
        pb = q - n * k;
        return 2; //两个交点
    }
 
    inline Point circle_center(const Point a, const Point b, const Point c)
    {
        Point center;
        ld a1 = b.x - a.x, b1 = b.y - a.y, c1 = (a1 * a1 + b1 * b1) / 2;
        ld a2 = c.x - a.x, b2 = c.y - a.y, c2 = (a2 * a2 + b2 * b2) / 2;
        ld d = a1 * b2 - a2 * b1;
        center.x = a.x + (c1 * b2 - c2 * b1) / d;
        center.y = a.y + (a1 * c2 - a2 * c1) / d;
        return center;
    }
 
    //最小覆盖圆
    inline void min_cover_circle(Point* p, const int n, Point& c, ld& r)
    {
        random_shuffle(p, p + n);
        c = p[0], r = 0;
        forn(i, 1, n - 1)
        {
            if (sign(Distance(p[i], c) - r) > 0)
            {
                c = p[i], r = 0;
                forn(j, 0, i - 1)
                {
                    if (sign(Distance(p[j], c) - r) > 0)
                    {
                        c.x = (p[i].x + p[j].x) / 2;
                        c.y = (p[i].y + p[j].y) / 2;
                        r = Distance(p[j], c);
                        forn(k, 0, j - 1)
                        {
                            if (sign(Distance(p[k], c) - r) > 0)
                            {
                                c = circle_center(p[i], p[j], p[k]);
                                r = Distance(p[i], c);
                            }
                        }
                    }
                }
            }
        }
    }
}
 
namespace Geometry3D
{
    //精度
    constexpr ld eps = 1e-12;
    //Π
    const ld PI = acos(-1.0);
 
    ld sgn(const ld x)
    {
        if (!fabs(x)) return 0;
        return x / fabs(x);
    }
 
    ////三维:点
    struct Point3
    {
        ld x{}, y{}, z{};
 
        Point3() = default;
 
        Point3(const ld x, const ld y, const ld z) : x(x), y(y), z(z)
        {
        }
 
        Point3 operator+(const Point3 B) const
        {
            return Point3{x + B.x, y + B.y, z + B.z};
        }
 
        Point3 operator-(const Point3 B) const
        {
            return Point3{x - B.x, y - B.y, z - B.z};
        }
 
        Point3 operator*(const double k) const
        {
            return Point3{x * k, y * k, z * k};
        }
 
        Point3 operator/(const double k) const
        {
            return Point3{x / k, y / k, z / k};
        }
 
        bool operator==(const Point3 B) const
        {
            return sgn(x - B.x) == 0 && sgn(y - B.y) == 0 && sgn(z - B.z) == 0;
        }
    };
 
    typedef Point3 Vector3;
 
    //点积.和二维点积函数同名.C++允许函数同名
    inline ld Dot(const Vector3& A, const Vector3& B)
    {
        return A.x * B.x + A.y * B.y + A.z * B.z;
    }
 
    //叉积
    inline Vector3 Cross(const Vector3& A, const Vector3& B)
    {
        return Point3{A.y * B.z - A.z * B.y, A.z * B.x - A.x * B.z, A.x * B.y - A.y * B.x};
    }
 
    inline ld Len(const Vector3& A)
    {
        return sqrt(Dot(A, A));
    } //向量的长度
    inline ld Len2(const Vector3& A)
    {
        return Dot(A, A);
    } //向量长度的平方
    //A、B的距离
    inline ld Distance(const Point3& A, const Point3& B)
    {
        return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y) + (A.z - B.z) * (A.z - B.z));
    }
 
    //A与B的夹角
    inline ld Angle(const Vector3& A, const Vector3& B)
    {
        return acos(Dot(A, B) / Len(A) / Len(B));
    }
 
    //三维:线
    struct Line3
    {
        Point3 p1, p2;
 
        Line3() = default;
 
        Line3(const Point3& p1, const Point3& p2) : p1(p1), p2(p2)
        {
        }
    };
 
    typedef Line3 Segment3; //定义线段,两端点是Point p1,p2
    //三维:三角形面积的两倍
    inline ld Area2(const Point3& A, const Point3& B, const Point3& C)
    {
        return Len(Cross(B - A, C - A));
    }
 
    //三维:点到直线的距离
    inline ld Dis_point_line(const Point3& p, const Line3& v)
    {
        return Len(Cross(v.p2 - v.p1, p - v.p1)) / Distance(v.p1, v.p2);
    }
 
    //三维:点在直线上
    inline bool Point_line_relation(const Point3& p, const Line3& v)
    {
        return sgn(Len(Cross(v.p1 - p, v.p2 - p))) == 0 && sgn(Dot(v.p1 - p, v.p2 - p)) == 0;
    }
 
    //三维:点到线段的距离
    inline ld Dis_point_seg(const Point3& p, const Segment3& v)
    {
        if (sgn(Dot(p - v.p1, v.p2 - v.p1)) < 0 || sgn(Dot(p - v.p2, v.p1 - v.p2)) < 0)
            return min(
                Distance(p, v.p1), Distance(p, v.p2));
        return Dis_point_line(p, v);
    }
 
    //三维:点p在直线上的投影
    inline Point3 Point_line_proj(const Point3& p, const Line3& v)
    {
        double k = Dot(v.p2 - v.p1, p - v.p1) / Len2(v.p2 - v.p1);
        return v.p1 + (v.p2 - v.p1) * k;
    }
 
    //三维:平面
    struct Plane
    {
        Point3 p1, p2, p3; //平面上的三个点
        Plane() = default;
 
        Plane(const Point3& p1, const Point3& p2, const Point3& p3) : p1(p1), p2(p2), p3(p3)
        {
        }
    };
 
    //平面法向量
    inline Point3 PVec(const Plane& f)
    {
        return Cross(f.p2 - f.p1, f.p3 - f.p1);
    }
 
    //四点共平面
    inline bool Point_on_plane(Point3 A, Point3 B, Point3 C, const Point3& D)
    {
        return sgn(Dot(PVec({A, B, C}), D - A)) == 0;
    }
 
    //两平面平行
    inline int Parallel(const Plane& f1, const Plane& f2)
    {
        return Len(Cross(PVec(f1), PVec(f2))) < eps;
    }
 
    //两平面垂直
    inline int Vertical(const Plane& f1, const Plane& f2)
    {
        return sgn(Dot(PVec(f1), PVec(f2))) == 0;
    }
 
    //直线与平面的交点p,返回值是交点的个数
    inline int Line_cross_plane(const Line3& u, const Plane& f, Point3& p)
    {
        Point3 v = PVec(f); //平面的法向量
        double x = Dot(v, u.p2 - f.p1);
        double y = Dot(v, u.p1 - f.p1);
        double d = x - y;
        if (sgn(x) == 0 && sgn(y) == 0) return -1; //-1:v在f上
        if (sgn(d) == 0) return 0; //0:v与f平行
        p = (u.p1 * x - u.p2 * y) / d; //1:v与f相交
        return 1;
    }
 
    //四面体有向面积*6
    inline double volume4(const Point3& A, const Point3& B, const Point3& C, const Point3& D)
    {
        return Dot(Cross(B - A, C - A), D - A);
    }
}
 
namespace Matrix
{
    constexpr int NNN = 101;
    ll MOD = 1e9 + 7;
 
    struct Matrix
    {
        ll a[NNN][NNN];
 
        Matrix operator*(const Matrix& other) const
        {
            Matrix ans;
            memset(ans.a, 0, sizeof ans.a);
            forn(i, 1, NNN - 1)
                forn(j, 1, NNN - 1)
                    forn(k, 1, NNN - 1)
                        ans.a[i][j] = modt(
                            ans.a[i][j] + a[i][k] * other.a[k][j] % MOD, MOD);
            return ans;
        }
    };
 
    inline Matrix qpow(Matrix curr, ll k)
    {
        Matrix ans;
        memset(ans.a, 0, sizeof ans.a);
        forn(i, 1, NNN - 1) ans.a[i][i] = 1;
        for (; k; k >>= 1, curr = curr * curr) if (k & 1) ans = ans * curr;
        return ans;
    }
}
 
namespace SuffixArray
{
    constexpr int N = 1e6 + 10; //数组大小
    constexpr int BUKSize = 128; //初始桶的个数
    int sa[N], rnk[N], h[N]; //后缀数组
    char s[N]; //字符串
    int n; //字符串长
    //两个类型
    enum STR
    {
        L, S
    };
 
    //判断是否是LMS,当前位为S型,左边一位为L型
    bool isLMS(auto type, int pos)
    {
        return !(pos == 0 || type[pos] != STR::S || type[pos - 1] != STR::L);
    }
 
    //判断是否是相等的LMS
    bool isSameLMS(auto str, auto type, const int i, const int j)
    {
        if (i == -1 || j == -1) return false;
        int k = -1;
        while (true)
        {
            ++k;
            if (str[i + k] != str[j + k] || type[i + k] != type[j + k]) return false; //如果对应字符不等,或者类型不等
            if (k == 0) continue;
            if (isLMS(type, i + k) != isLMS(type, j + k)) return false;
            if (isLMS(type, i + k)) return true;
        }
    }
 
    //诱导排序LLLLLSSSSSS
    void inSort(auto str, auto len, auto type, auto LMS, auto lmsSize, const int currBukSize)
    {
        auto buck = new int[currBukSize]; //桶
        auto pre = new int[currBukSize]; //桶前缀和
        memset(buck, 0, sizeof(buck[0]) * currBukSize);
        memset(pre, 0, sizeof(pre[0]) * currBukSize);
        memset(sa, -1, sizeof(int) * len);
        forn(i, 0, len - 1) ++buck[str[i]]; //字符分桶
        pre[0] = buck[0];
        forn(i, 1, currBukSize - 1) pre[i] = pre[i - 1] + buck[i]; //前缀和
        //先处理LMS(特殊的S型)到S桶里
        forv(i, lmsSize - 1, 0) sa[--pre[str[LMS[i]]]] = LMS[i];
        //正逆序扫,分S型和L型两种桶进行排序SSSSSSLLLLLLLL
        //顺序处理L型
        pre[0] = 0;
        forn(i, 1, currBukSize - 1) pre[i] = pre[i - 1] + buck[i - 1];
        forn(i, 0, len - 1) if (sa[i] > 0 && type[sa[i] - 1] == STR::L) sa[pre[str[sa[i] - 1]]++] = sa[i] - 1;
        //逆序处理S型
        pre[0] = buck[0];
        forn(i, 1, currBukSize - 1) pre[i] = pre[i - 1] + buck[i]; //前缀和
        forv(i, len - 1, 0) if (sa[i] > 0 && type[sa[i] - 1] == STR::S) sa[--pre[str[sa[i] - 1]]] = sa[i] - 1;
        delete[] buck;
        delete[] pre;
    }
 
    //SA-IS
    void SA_IS(auto str, int len, auto LMS, int currBukSize)
    {
        auto type = new STR[N + 1];
        //默认最后增加一个字符'#'比任何字符小,所以最后一个字符为S型
        //处理类型
        //前后相等用性质否则用定义
        type[len - 1] = STR::S;
        forv(i, len - 2, 0) type[i] = str[i] == str[i + 1] ? type[i + 1] : str[i] < str[i + 1] ? STR::S : STR::L;
        int lmsSize = 0;
        forn(i, 0, len - 1) if (isLMS(type, i)) LMS[lmsSize++] = i;
        inSort(str, len, type, LMS, lmsSize, currBukSize); //诱导排序S型和L型
        int pre = -1; //上一个sa[i]
        int cnt = 0;
        auto tmp = new int[len]; //临时存值数组
        //记录还无法确定次序的LMS数组,还未确定次序就递归排序
        forn(i, 0, len - 1)
        {
            if (!isLMS(type, sa[i])) continue;
            if (!isSameLMS(str, type, pre, sa[i])) ++cnt;
            tmp[sa[i]] = cnt - 1;
            pre = sa[i];
        }
        auto nxtStr = new int[lmsSize];
        lmsSize = 0;
        //记录LMS
        forn(i, 0, len - 1)
        {
            if (!isLMS(type, i)) continue;
            nxtStr[lmsSize++] = tmp[i];
        }
        delete[] tmp;
        auto nxtLMS = new int[lmsSize];
        if (cnt < lmsSize) SA_IS(nxtStr, lmsSize, nxtLMS, cnt);
        else
            forn(i, 0, lmsSize - 1) sa[nxtStr[i]] = i;
        delete[] nxtStr;
        forn(i, 0, lmsSize - 1) nxtLMS[i] = LMS[sa[i]];
        inSort(str, len, type, nxtLMS, lmsSize, currBukSize);
        delete[] nxtLMS;
        delete[] type;
    }
 
    inline void init(const int len)
    {
        n = len;
        auto LMS = new int[n];
        //加一个字符'#'
        SA_IS(s, n + 1, LMS, BUKSize);
        delete[] LMS;
        forn(i, 0, n - 1) sa[i] = sa[i + 1] + 1;
        forv(i, n - 1, 0) swap(sa[i], sa[i + 1]), swap(s[i], s[i + 1]);
        sa[0] = sa[n + 1] = 0;
    }
 
    void get_h()
    {
        forn(i, 1, n) rnk[sa[i]] = i;
        for (int i = 1, k = 0; i <= n; i++)
        {
            if (rnk[i] == 1) continue;
            if (k) k--; //大于等于上一个后缀的h-1
            int ear = sa[rnk[i] - 1]; //上一个后缀
            while (i + k <= n && ear + k <= n && s[i + k] == s[ear + k]) k++;
            h[rnk[i]] = k;
        }
    }
 
    inline void clear()
    {
        forn(i, 0, n) sa[i] = rnk[i] = h[i] = 0;
        forn(i, 0, n) s[i] = '\0';
    }
}
 
using namespace Geometry2D;
// using namespace Geometry3D;
// using namespace Matrix;
// using namespace SuffixArray;
constexpr int T = 5;
constexpr int N = T + 10;
ld r, s[N], e[N];
 
inline ld getVal(const ld ans)
{
    return ans * PI / 180;
}
 
inline int idx(const int curr)
{
    if (curr <= 0) return curr + T;
    if (curr > T) return curr - T;
    return curr;
}
 
inline Point pos(const ld angle)
{
    return Point(r * cos(angle), r * sin(angle));
}
 
inline ld getAngle(const ld ans)
{
    if (ans < 0) return ans + 2 * PI;
    return ans;
}
 
inline void solve()
{
    cin >> r;
    forn(i, 1, T) cin >> s[i], s[i] = getVal(s[i]);
    forn(i, 1, T) cin >> e[i], e[i] = getVal(e[i]);
    ld ans = 0;
    forn(i, 1, T)
    {
        const int idx1 = i, idx2 = idx(i + 1), idx3 = idx(i - 1), idx4 = idx(i - 2);
        const Point p1 = pos(s[idx1]);
        const Point p2 = pos(s[idx2]);
        const Point p3 = pos(e[idx3]);
        const Point p4 = pos(e[idx4]);
        //p1-p4 与 p2-p3 的交点
        const Point point = Cross_point(p1, p4, p2, p3);
        ans += fabs(Area2(p1, point, p3)) / 2; //三角形面积
        const ld angele = getAngle(s[idx1] - e[idx3]); //夹角度数
        ans += pow(r, 2) / 2 * (angele - sin(angele)); //弓形面积
    }
    cout << PI * pow(r, 2) - ans << endl;
}
 
signed int main()
{
    Spider
    //------------------------------------------------------
    cout << fixed << setprecision(10);
    int test = 1;
    //    read(test);
    cin >> test;
    forn(i, 1, test) solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
}

单次询问时间复杂度为：$O(1)$