P3939 数颜色 题解

题目链接：数颜色

经典题目了，暴力数据结构随便过，不过这种不带修的单个颜色的数量查找有个经典的做法：分桶+二分。具体的为每个颜色分桶，记录有序下标，这样就可以二分出 \([l,r]\) 上的下标个数。对于一次交换来说，如果相邻的颜色相同那么并不会发生交换，如果不同那么就发生交换，由于下标在桶里，我们还需要同时维护桶内下标所在的有序下标序列编号 \(id\)，交换时需要将二者交换了，即交换二者所在的桶，由于下标不断往前往后一定会触碰到与之相同颜色的下标，而我们相同颜色选择不交换，这样并不会发生下标次序跨越，即跑到有序序列中对应的位置前面或者后面下标的其他地方。

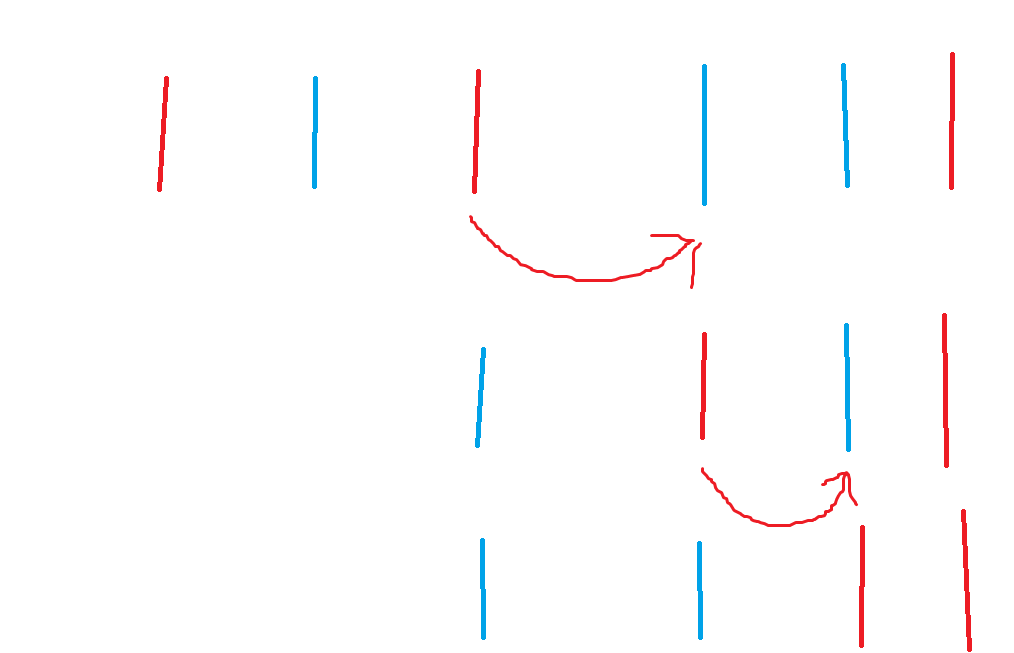
如图，其实每个颜色的下标只会在 \([前一个相同颜色的下标,后一个颜色相同的下标]\) 的范围移动，并不会越界。所以我们的交换只需要交换上述提到的 \(id\) 对应的下标，以及 \(id\) 和数组值即可。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}


template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 3e5 + 10;
vector<int> pos[N];
int id[N];
int n, m;
int a[N];

inline void solve()
{
    cin >> n >> m;
    forn(i, 1, n)
    {
        cin >> a[i];
        id[i] = pos[a[i]].size();
        pos[a[i]].push_back(i);
    }
    while (m--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int l, r, c;
            cin >> l >> r >> c;
            const auto& curr = pos[c];
            if (curr.empty() or curr.front() > r or curr.back() < l)
            {
                cout << 0 << endl;
                continue;
            }
            const int R = ranges::upper_bound(all(curr), r) - curr.begin();
            const int L = ranges::lower_bound(all(curr), l) - curr.begin();
            cout << R - L << endl;
        }
        else
        {
            int x;
            cin >> x;
            if (a[x] != a[x + 1])
            {
                const int c1 = a[x], c2 = a[x + 1];
                swap(pos[c1][id[x]], pos[c2][id[x + 1]]);
                swap(id[x], id[x + 1]);
                swap(a[x], a[x + 1]);
            }
        }
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[最坏时间复杂度为:\ O(m\log{n}) \]