值域分块系统级教学
确保你已经会普通的分块和常见的线段树之类的知识点。
值域分块背景阐述
在树类，我们都有一类特殊的树---权值树。传统的，无论是线段树还是树状数组之类的，我们都是以序列下标所在的序列轴作为核心轴维护对象，维护的信息即为序列轴上的数。而权值树是一类特殊的树，它的轴则是数轴，数轴上的数则表示当前数的个数。你可以当做一个桶，去维护了每个元素个数，区别于常规的桶而言，它自带了一个特点----自带有序，数轴上的数都是从小到大排列的，这意味着具有单调性，也意味着我们可以 “二分答案”。所以我们常见的有，权值线段树，它的 \([l,r]\) 表示的不再是数组下标位于 \([l,r]\) 的数，而是值域位于 \([l,r]\) 的数，维护的即为这个上面的数的数量，或者总和之类的信息。权值树状数组也比较常用，离散化值域后，权值树状数组最常见的应用自然是---计算逆序对。在分块界有没有对应的东西？有，答案是------值域分块。
这个常常出现于 ynoi 题目的东西，在本篇文章，详细地进行介绍它的特点与常见使用。类比线段树，我们常见的普通分块，我们称之为 序列分块，它和普通线段树是大同小异的，包括打 lazy 之类的技巧，根号重构之类的。而普通的分块是基于序列轴分块，值域分块则是基于数轴分块，假如值域为 \([1,MX]\)，比如 \([1,10]\)，\(\sqrt{10}=3\)，那么值域分块结果为：\([1,3],[4,6],[7,9],[10,10]\)。
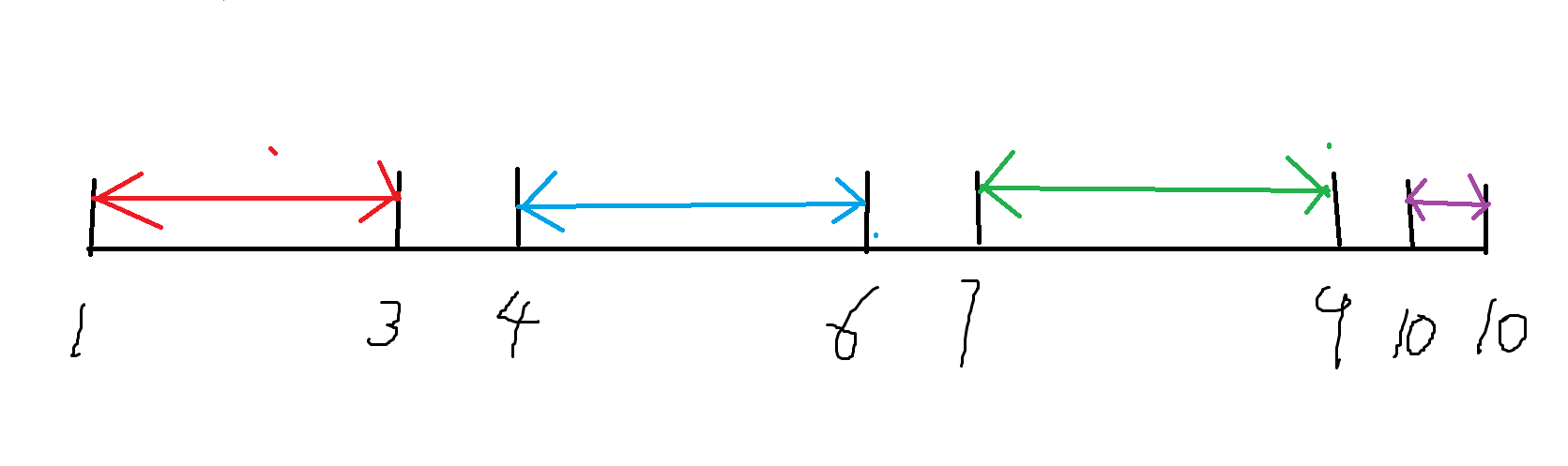
如图所示，这样就将值域分成了若干个值域块，每个块我们就可以维护两个信息：
-
块整体信息，比如块整体的数量个数，和之类的信息，跟权值线段树一致。
-
单点信息，单点情况。
我们关注到基于分块思想，这有两个特点：
-
值域块数量为 \(\sqrt{MX}\) 级别。
-
每个值域块内的数的个数为 \(\sqrt{MX}\) 级别。
那么来一个最简单的功能，询问 \(val\ 处于\ [l,r]\) 上的数量有多少个？这个很显然，我们找到 \(l\) 和 \(r\) 所在的值域块，基于分块的基本操作：
-
同一值域块暴力统计。
-
不同的块，整个值域块直接获取信息，散块暴力。
这样一来 \(\sqrt{MX}\) 级别的 “权值树” 我们就有了。常常我们离散化后值域与 \(n\) 即序列是一个数量级的，所以 \(n\sqrt{n}\) 的权值树拿到了！！！
两种常用的值域分块
如果只是权值树的基本功能，那也太捞了，我为啥要用值域分块？不能直接权值线段树？讲讲带上修改的的两种值域分块。需要维护前缀和这样的东西。
这里基于最基本的操作，单修区查讨论，即插入或者删除某个数，查询一段值域的数的个数。
- 值域分块以后，只维护值域块的基本信息。也就是我们刚刚说的最基本的分块，我们很容易发现：修改是 \(O(1)\) 的，值需要对应修改值域块整体信息 (和标记永久化一个道理),和单点修改，单点修改很简单，常常我们开一个数组模拟桶就行。
参照代码
constexpr int N = 1e5 + 10;
int valCnt[N]; //每个值域块的元素个数
int cnt[N]; //单点贡献
int pos[N], s[N], e[N]; //每个值的值域块编号,每个块的起点和终点
inline void add(const int val, const int change)
{
const int id = pos[val];
valCnt[id] += change, cnt[val] += change;
}
inline int query(const int l, const int r)
{
const int L = pos[l], R = pos[r];
int ans = 0;
if (L == R)
{
forn(i, l, r)ans += cnt[i];
return ans;
}
forn(i, l, e[L])ans += cnt[i];
forn(i, s[R], r)ans += cnt[i];
forn(i, L+1, R-1)ans += valCnt[i];
return ans;
}
我们发现这种值域分块的特点：
- 有没有反过来的？有，我们维护值域块的前缀和，以及每个值域块内也维护前缀和，这样修改和查询就反过来了，我们为每个值域块每个位置维护它在值域块内的编号。
参照代码
constexpr int N = 1e5 + 10;
constexpr int SIZE = sqrt(N); //值域块最大大小
constexpr int CNT = (N + SIZE - 1) / SIZE + 10; //值域块最大数量
int preVal[N]; //值域块的前缀和,即[1,i]的值域块元素数量和或者其他信息
int prePos[CNT][SIZE]; //每个值域块内的前缀和,即在值域块内的[1,i]元素的前缀数量和
int pos[N], idx[N], s[N], e[N]; //每个值的值域块编号,每个值在值域块内的位置从1开始,范围为[1,SIZE],块起点和终点
int cnt; //值域块数量
inline void add(const int val, const int change)
{
const int id = pos[val];
forn(i, id, cnt)preVal[i] += change; //值域块前缀和暴力更新
forn(i, idx[val], e[id])prePos[id][i] += change; //块内前缀和更新
}
inline int query(const int l, const int r)
{
const int L = pos[l], R = pos[r];
int ans = 0;
//[L+1,R-1]用值域整块前缀和计算
if (R - L > 1)ans += preVal[R - 1] - preVal[L];
//散块算两个前缀和
ans += prePos[R][idx[r]]; //块内[1,idx[r]]
ans += prePos[L][idx[e[L]]] - prePos[L][idx[l] - 1]; //块内[idx[l],idx[e[L]]]
return ans;
}
当然如果方便写的话，维护后缀和也行。总之采用前缀和思想即可，我们观察到更新，最多遍历所有值域块，以及单个值域块内部所有数，所以复杂度是 \(\sqrt{MX}\)。
我们发现这种值域分块的特点：
很有特点是不是，这两个值域分块应用场景常常为平衡复杂度。我们注意树类的 ds 常常是修改和查询都是 \(log\) 级别。有些场景可能某一个并不需要那么优秀。
举例子：
莫队的修改我们需要 \(O(1)\)，而 \(q\) 次查询，并不需要 \(\log{MX}\) 这么优秀，离散化值域以后我们的 \(MX=n\)，这个时候我们可以用值域分块来平衡复杂度，使得修改和查询总复杂度都来到了 \(m\sqrt{n}\)。完美的平衡复杂度。这个时候用的则是修改 \(O(1)\)，查询 \(O(\sqrt{n})\) 来平衡的。
根号分治，关于小块的，常常我们用一些 ds 来解决问题。这里面有 \(\sqrt{n}\) 个数需要考虑贡献，当然值域分块还是离散化后的整个 \([1,n]\) 的，每次查询，要考虑 \(\sqrt{n}\) 个数每个的贡献情况，如果的每个数查询是 \(\log{n}\)，那么最坏则为 \(n\sqrt{n}\log{n}\)，完全不行。观察到每次只需要修改一个数的贡献，最多修改 \(q\) 次操作。那么这个时候则需要 \(O(1)\) 查询，\(O(\sqrt{n})\) 修改。这个时候显然用另一种值域分块最合适，这样修改和查询也都被平衡到了 \(q\sqrt{n}\) 了。
序列分块套值域分块
值域分块显然也是支持类似二分求答案的，枚举值域块，然后枚举单点，\(2\sqrt{MX}\) 就能完成类似二分求答案。比如最常见的全局第 \(k\) 大，权值树二分太简单了，值域块我们考虑当前这个值域块加上数量是否足够，不够继续枚举，否则枚举当前值域块单点确定答案，值域显然是单增，满足单调性。
在分块界，是否有树套树这种东西，显然是有的，序列分块套值域分块。我们说点常用的套权值树比较特殊的：解决差分性问题的主席树，怎么用这个代替。有个问题：静态主席树不支持修改，所以要支持修改，我们需要使用树状数组套权值树来实现 \(O(\log^2{n})\) 级别的操作，这类特点是空间需求大。序列分块套值域分块怎么实现这样的可差性问题基本操作，引用我的 这篇文章，我在里面的第三种方法提到了需要维护的常见信息。
其实只需要注意到：
序列分块和值域分块，都有需要的散块需要注意。
具体我们维护，\(pre[i][j]=pre[序列块编号][前缀值域块]的元素数量\)，预处理分两步：
-
对每个序列块，处理出它对应的值域块情况。
-
对每个序列块的值域块做一遍前缀和。
有时候可能我们会维护再带上前缀序列块的前缀和。对前缀序列块的每个值域块做前缀和。
参照代码
constexpr int N = 2e5 + 10;
ll a[N];
int pos[N], s[N], e[N];
int n, q, mx;
constexpr int SIZE = sqrt(N);
constexpr int CNT = (N + SIZE - 1) / SIZE;
int pre[CNT + 1][N];
int cnt; //离散化后序列分块/值域分块数量
inline void solve()
{
forn(i, 1, cnt)
{
forn(j, s[i], e[i])pre[i][a[j]]++;//值域块修改
forn(j, 1, mx)pre[i][j] += pre[i][j - 1];//值域块前缀和
}
}
这样处理完以后，对于查询，我们就可以很简单地做到哦统计 \([l,r]\) 上值域为 \([L,R]\) 的数了，以 \(\sqrt{n}\) 级别统计，只需要对每个值域块进行前缀和做差，非整块暴力即可。
这样套面对无修改的题都很容易，但带上修改以后，你会发现，每个序列块的值域块都要修改，复杂度就高了，所以这玩意你可以当做静态主席树，想想静态主席树是不是维护内层和的前缀和？想想怎么带上修改的，外层套个 BIT，BIT 维护序列上的前缀和。
所以要带上修改很简单，我们改为维护前缀序列块的某个值域块前缀和 \(pre[i][j]=pre[前缀序列块][值域块编号]的元素数量\)。写法很简单了,当然同时维护，前缀序列块的单点和数量。
参照代码
constexpr int N = 2e5 + 10;
ll a[N];
int pos[N], s[N], e[N];
int n, q, mx;
constexpr int SIZE = sqrt(N);
constexpr int CNT = (N + SIZE - 1) / SIZE;
int pre[CNT + 1][N], preCnt[CNT + 1][N]; //前缀值域块和,前缀单点数量
int cnt; //离散化后序列分块/值域分块数量
inline void solve()
{
forn(i, 1, cnt)
{
forn(j, 1, CNT)pre[i][j] += pre[i - 1][j]; //前缀值域块统计
forn(j, 1, n)preCnt[i][j] += preCnt[i - 1][j]; //前缀单点统计
forn(j, s[i], e[i])pre[i][pos[a[j]]]++, preCnt[i][a[j]]++; //值域块修改
}
}
这样做的好处，先来考虑，单点修改，单点增加或者删除掉某个位置的数，我们只需要更新前缀序列块的信息即可。
修改参照代码
//curr位置,val=+1是增加一个数,-1是删除一个数
inline void update(const int curr, const int val)
{
int valPos = pos[a[curr]]; //值域块编号
int blockPos = pos[curr]; //序列块编号
forn(i, blockPos, cnt) //更新从当前序列块到最后序列块前缀和
{
pre[i][valPos] += val; //对应值域块变化
preCnt[i][a[curr]] += val; //单点变化
}
}
这玩意你不觉得，就是使用修改 \(O(1)\) 的值域分块平衡了下修改复杂度，查询略复杂一些，具体看我代码：
查询参照代码
//查询[l,r]上值域位于[L,R]的元素个数
inline int query(const int l, const int r, const int minVal, const int maxVal)
{
const int L = pos[l], R = pos[r];
const int valL = pos[minVal], valR = pos[maxVal];
int ans = 0;
if (L + 1 <= R - 1)
{
//序列块整块部分的贡献
//值域块整块部分贡献
forn(i, valL+1, valR-1)ans += pre[R - 1][i] - pre[L][i];
//值域块散块贡献
forn(i, minVal, e[valL])ans += preCnt[R - 1][i] - preCnt[L][i];
forn(i, s[maxVal], maxVal)ans += preCnt[R - 1][i] - preCnt[L][i];
}
forn(i, l, e[L])ans += minVal <= a[i] and a[i] <= maxVal;
forn(i, s[R], r)ans += minVal <= a[i] and a[i] <= maxVal;
return ans;
}
很明显的，这里只需要枚举值域块的贡献即可，序列块的贡献可以直接使用前缀和做差拿到一系列整块的序列块答案，不需要枚举序列块了，这个其实就是我们的 \(O(1)\) 修改值域块，\(O(\sqrt{n})\) 查询值域块答案的方法。这样一来，它空间很小，常数小，没有太多迭代，速度媲美 \(O(\log^2{n})\) 的带修树套树，树套树这个常数不小，所以这玩意常数常常可以吊打树套树。
后记
这仅仅也是根号科技里面的常用教学。关于根号科技显然有很多优化方式，例如分散层叠算法优化有序块问题，即块内要保证有序方便统计与二分。关于带修第 \(k\) 大问题，我们的序列分块套值域分块，只需要将序列散块单点信息放入桶中，这个桶包括了一个临时的值域分块桶和单点桶，枚举值域块，可以轻松地拿到 \([l,r]\) 上的实际当前值域块情况了，具体的为整块信息加上散块的对应的当前值域块信息即可。一直到单点同理，和全局 \(kth\) 是一个道理的。
