CF916E Jamie and Tree 题解

题目链接：CF 或者洛谷

本题难点在于换根 LCA 与换根以后的子树范围寻找，重点讲解

先说操作一，假如原根为 $1$ 变为了 $x$，又变为了 $y$，那么其实 $y$ 和 $x$ 都可以看做由 $1$ 变化而来的，即 $1 \rightarrow x$ 与 $1 \rightarrow y$，原因很简单，我们可以把 $1 \rightarrow x$ 恢复成 $1$，再变为 $y$，这样换根的形态是没有发生任何变化的。所以这个操作我们可以直接换根。

第二个和第三个操作都可以总结为两步，找以当前为根的 $LCA$ 与子树在 $1$ 为根中的实际范围。

先说第一个如何找 $LCA$，其实分讨下容易发现，分 $x$ 与 $y$ 与 $root$ 原来是否具有子树关系：

都是 $root$ 为根的子树上的点，显然 $lca$ 即为 $root$。
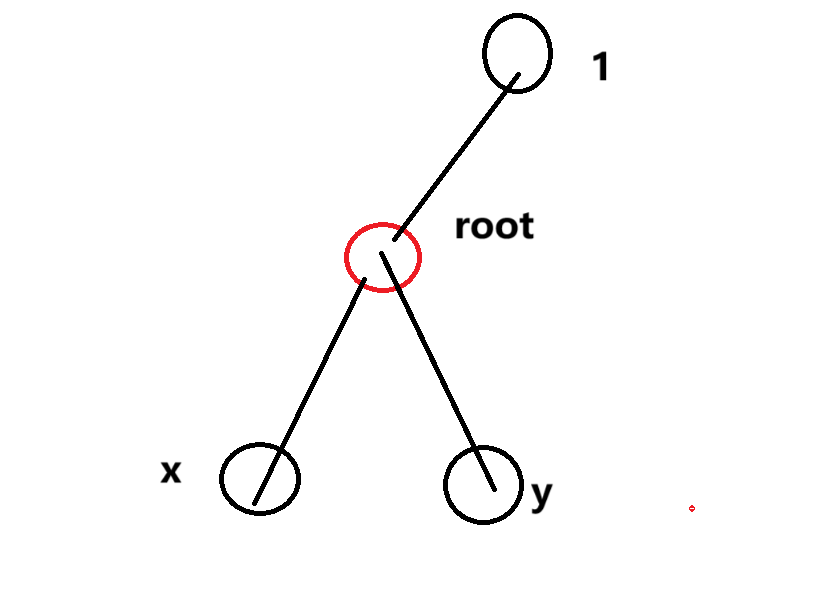
一个是子树上的，一个非子树上的。如图所示还是 $root$。

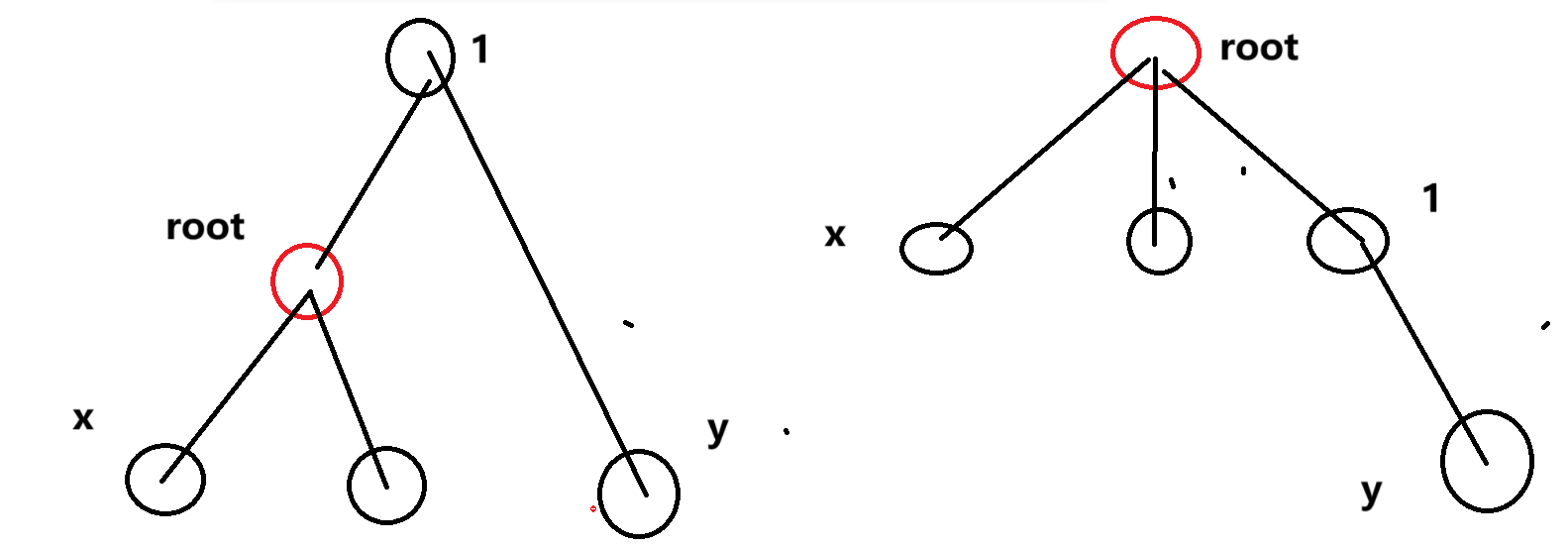
都不在子树里。

这个我们这样考虑，$t_1=lca(root,x)$，$t_2=lca(root,y)$，深度更深的那个，其实就是 lca，原因，这种情况下换根，$x$ 和 $y$ 的形态并未发生变化，而 $t1$ 和 $t2$ 其实就为以 $root$ 为根以后的 新子树节点，这个新子树节点包括了 $x$ 或者 $y$。根据第二种换根我们可以知道 $t1$ 或者 $t2$ 都有可以是 $lca$ 的祖先节点，而深度最深的那个显然为真正的 $lca$。

这三个情况可以统一成，我们再求出 $t_3=lca(x,y)$，那么 $t_1$、$t_2$、$t_3$ 中最深的点即为换根后的 $lca$，这也是动态 $lca$ 的基本套路。

接下来解决如何找到当前 $lca$ 子树范围在原序上的范围。

前两种情况显然 $lca=root$，换根后的子树范围即为 $[1,n]$ 包括了整棵树。

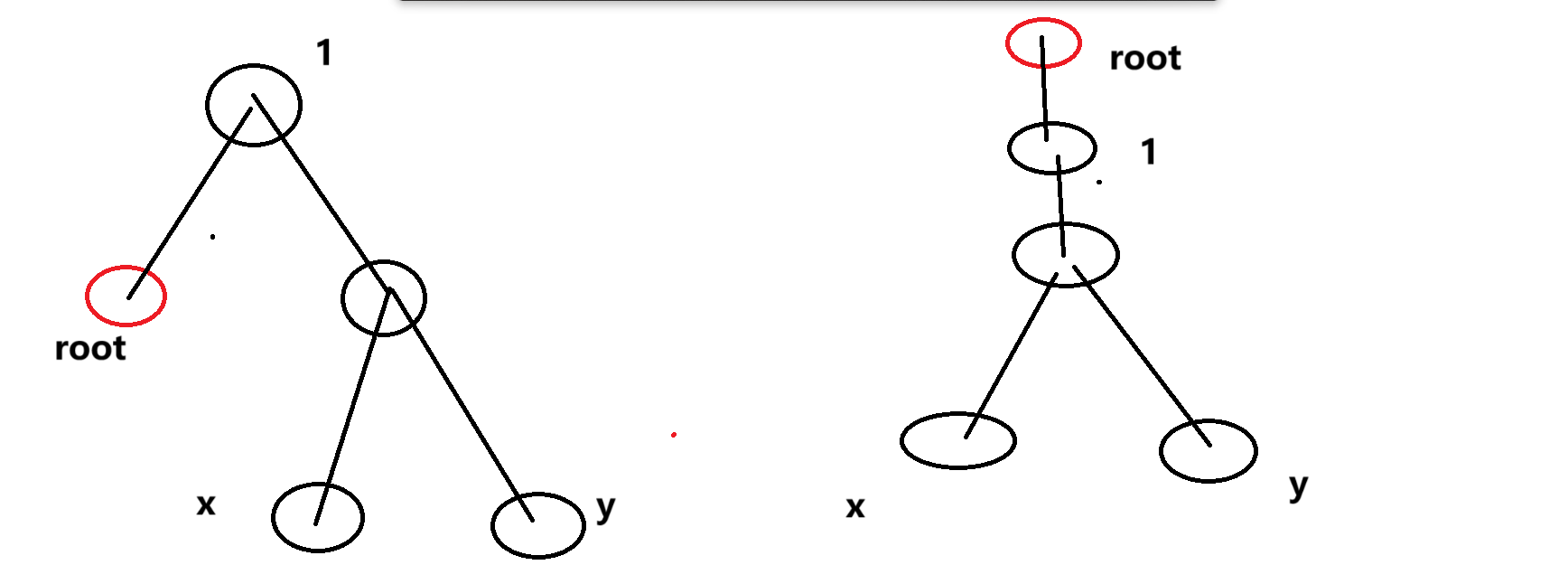
考虑第三种情况，分讨下，$lca$ 和 $root$ 的关系，显然就两种，$root$ 是否在 $lca$ 为根的子树内，一个在它子树当中，一个不在它子树当中。

不在子 $lca$ 为根的子树内，直接修改原子树即可。

子树形态是并未发生变化的。

在 $lca$ 为根的子树内，这个比较复杂，如图所示。

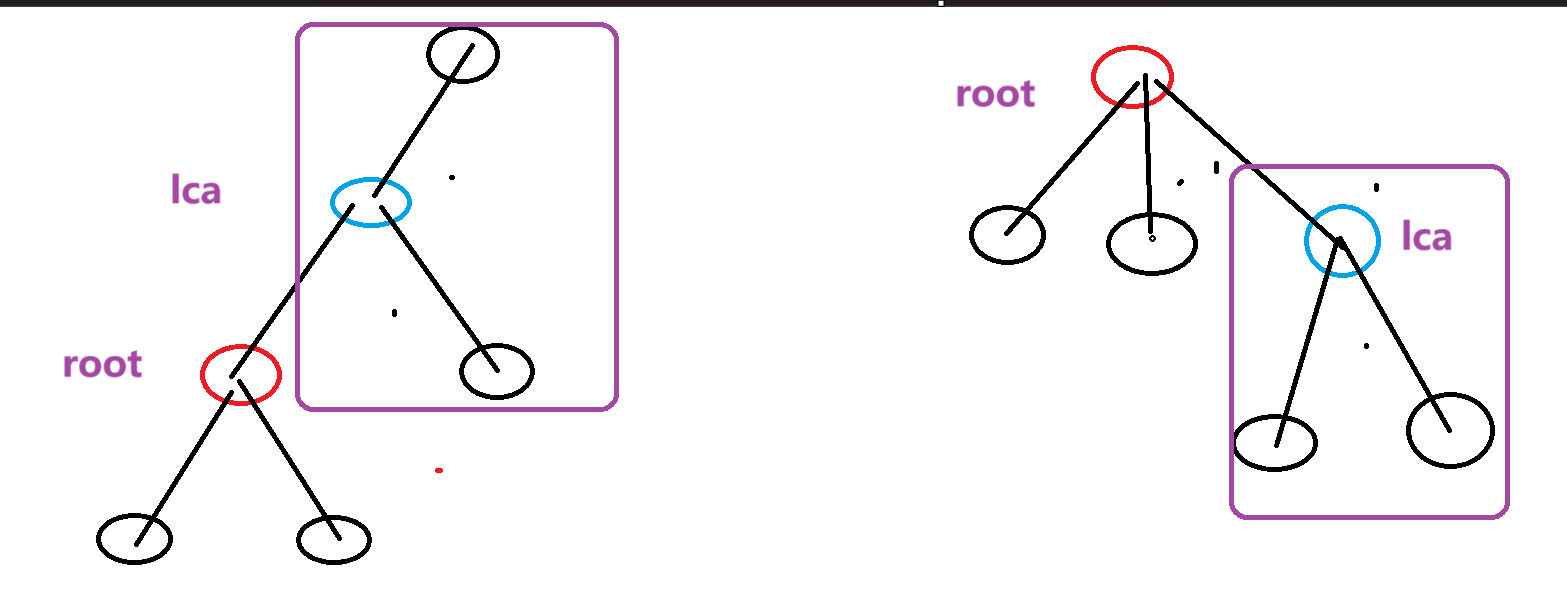
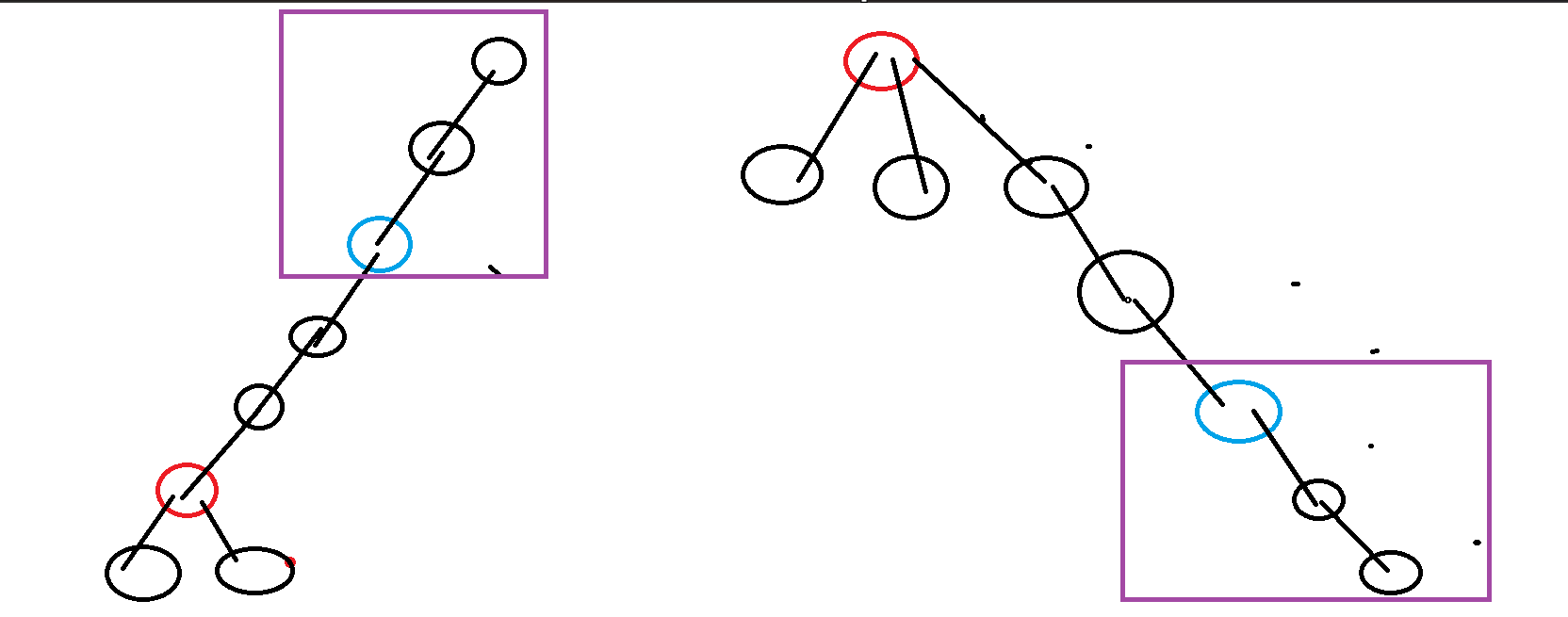
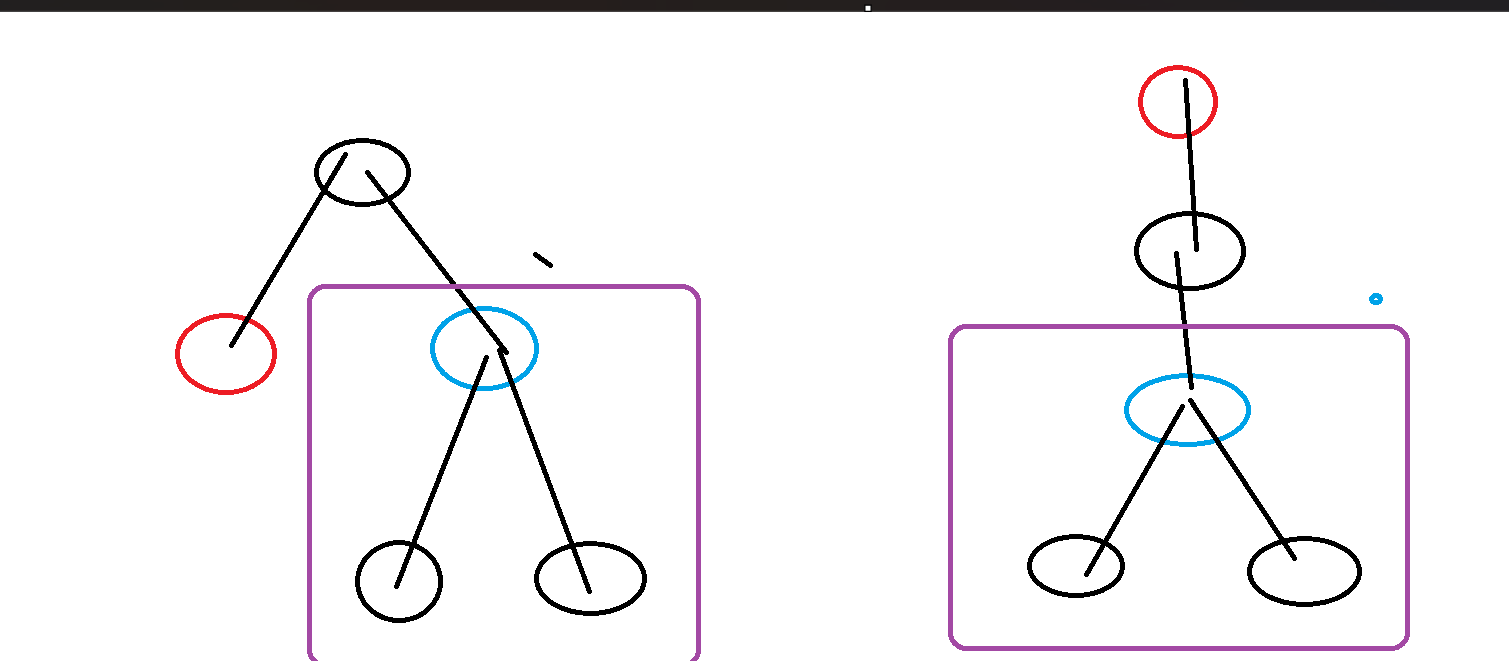
不得不说，太类似换根 dp 的套路，这玩意我们容斥来做，整棵树去掉 $lca$ 下面那个关键点为根的子树贡献即可。

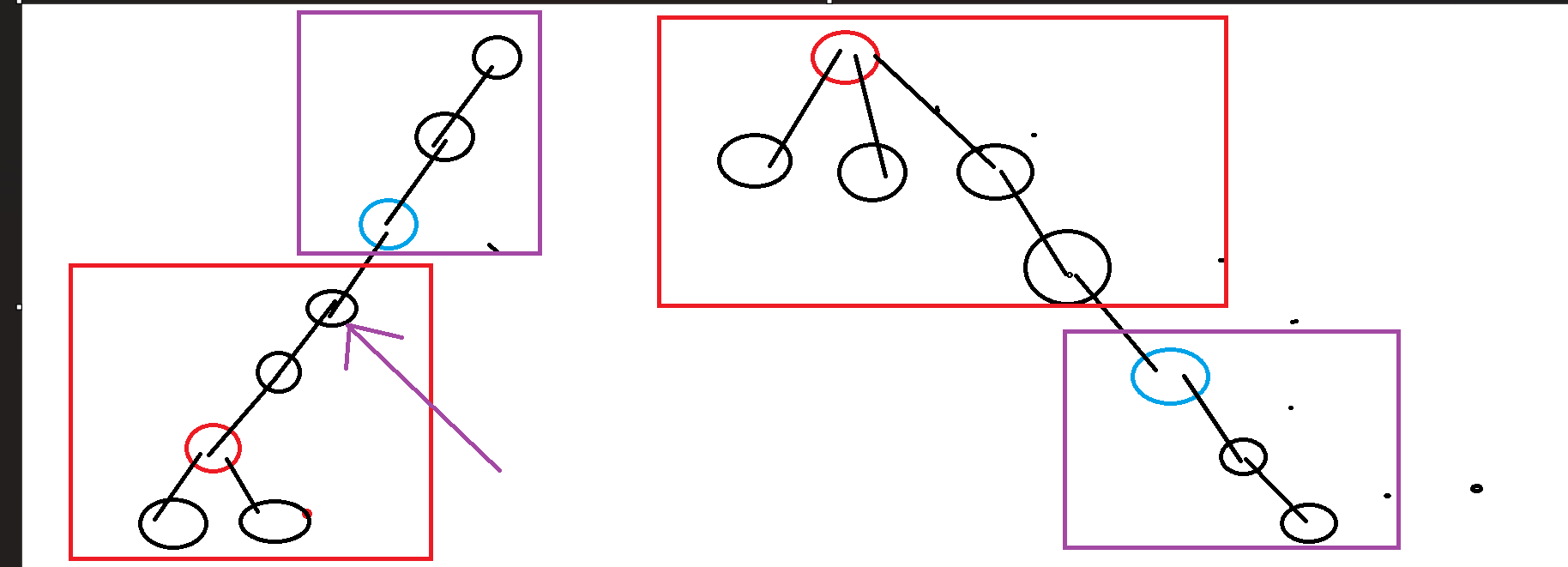
如图所示，全局加然后去掉红色部分贡献，即为正确的了，至于怎么找 $root \rightarrow lca$ 这条路径上的最后一个点，直接倍增找就行了。

解法一

涉及到了子树加，子树求和，我们使用 $dfs序+线段树$ 即可，当然区间加区间求和，也可以用差分树状数组，维护两个数组的 bit 即可，这里就用线段树了。当然由于是区间做加法，我们也可以用标记永久化线段树，不过这里就用普通线段树加懒标记即可。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}


template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 1e5 + 10;
constexpr int T = 20;
int s[N], e[N], dfn[N], cnt;
int deep[N], fa[N][T + 1];
int a[N], root = 1;
vector<int> child[N];
int n, q;

struct
{
    struct Node
    {
        ll sum, add, len;
    } node[N << 2];

#define len(x) node[x].len
#define add(x) node[x].add
#define sum(x) node[x].sum

    void Add(const int curr, const ll val)
    {
        add(curr) += val;
        sum(curr) += len(curr) * val;
    }

    void pushDown(const int curr)
    {
        if (add(curr))
        {
            Add(ls(curr),add(curr)), Add(rs(curr),add(curr));
            add(curr) = 0;
        }
    }

    void pushUp(const int curr)
    {
        sum(curr) = sum(ls(curr)) + sum(rs(curr));
    }

    void build(const int curr, const int l = 1, const int r = n)
    {
        len(curr) = r - l + 1;
        const int mid = l + r >> 1;
        if (l == r)
        {
            sum(curr) = a[dfn[l]];
            return;
        }
        build(ls(curr), l, mid);
        build(rs(curr), mid + 1, r);
        pushUp(curr);
    }

    void Add(const int curr, const int l, const int r, const int val, const int s = 1, const int e = n)
    {
        if (l <= s and e <= r)
        {
            Add(curr, val);
            return;
        }
        const int mid = s + e >> 1;
        pushDown(curr);
        if (l <= mid)Add(ls(curr), l, r, val, s, mid);
        if (r > mid)Add(rs(curr), l, r, val, mid + 1, e);
        pushUp(curr);
    }

    ll Query(const int curr, const int l, const int r, const int s = 1, const int e = n)
    {
        if (l <= s and e <= r)return sum(curr);
        pushDown(curr);
        const int mid = s + e >> 1;
        ll ans = 0;
        if (l <= mid)ans += Query(ls(curr), l, r, s, mid);
        if (r > mid)ans += Query(rs(curr), l, r, mid + 1, e);
        return ans;
    }
} seg;

inline void dfs(const int curr, const int parent)
{
    deep[curr] = deep[fa[curr][0] = parent] + 1;
    forn(i, 1, T)fa[curr][i] = fa[fa[curr][i - 1]][i - 1];
    dfn[++cnt] = curr;
    s[curr] = cnt;
    for (const auto nxt : child[curr])if (nxt != parent)dfs(nxt, curr);
    e[curr] = cnt;
}

inline int lca(int x, int y)
{
    if (deep[x] < deep[y])swap(x, y);
    forv(i, T, 0)if (deep[fa[x][i]] >= deep[y])x = fa[x][i];
    if (x == y)return x;
    forv(i, T, 0)if (fa[x][i] != fa[y][i])x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}

inline int LCA(const int x, const int y)
{
    const int t1 = lca(root, x), t2 = lca(root, y), t3 = lca(x, y);
    const int maxDeep = max({deep[t1], deep[t2], deep[t3]});
    if (maxDeep == deep[t1])return t1;
    if (maxDeep == deep[t2])return t2;
    return t3;
}

inline int top(int x, int k)
{
    while (k)
    {
        const int step = log2(k);
        x = fa[x][step];
        k -= 1 << step;
    }
    return x;
}

inline void Add(const int curr, const int val)
{
    if (curr == root)seg.Add(1, 1, n, val);
    else if (s[curr] <= s[root] and e[root] <= e[curr])
    {
        const int del = top(root, deep[root] - deep[curr] - 1);
        seg.Add(1, 1, n, val), seg.Add(1, s[del], e[del], -val);
    }
    else seg.Add(1, s[curr], e[curr], val);
}

inline ll Query(const int curr)
{
    if (curr == root)return seg.Query(1, 1, n);
    if (s[curr] <= s[root] and e[root] <= e[curr])
    {
        const int del = top(root, deep[root] - deep[curr] - 1);
        return seg.Query(1, 1, n) - seg.Query(1, s[del], e[del]);
    }
    return seg.Query(1, s[curr], e[curr]);
}

inline void solve()
{
    cin >> n >> q;
    forn(i, 1, n)cin >> a[i];
    forn(i, 1, n-1)
    {
        int u, v;
        cin >> u >> v;
        child[u].push_back(v), child[v].push_back(u);
    }
    dfs(1, 0);
    seg.build(1);
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)cin >> root;
        else if (op == 2)
        {
            int u, v, val;
            cin >> u >> v >> val;
            Add(LCA(u, v), val);
        }
        else
        {
            int curr;
            cin >> curr;
            cout << Query(curr) << endl;
        }
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

如果用Python 写的话，最好用一些常数小的东西，比如差分BIT 或者 zkw 线段树。

Python参照代码

import sys
from types import GeneratorType

input = lambda: sys.stdin.readline().strip()
print = lambda d: sys.stdout.write(str(d) + "\n")
M = lambda: map(int, input().split())
read = lambda: list(M())
N = 10 ** 5 + 10
T = 17
fa = [[0] * (T + 1) for _ in range(N)]
child = [[] for _ in range(N)]
deep = [0] * N
s, e, dfn = deep.copy(), deep.copy(), deep.copy()
cnt = 0
bit1, bit2 = deep.copy(), deep.copy()

lowBit = [0] * N
LOG2 = [0] * N


def bootstrap(f, stack=[]):
    def wrappedfunc(*args, **kwargs):
        if stack:
            return f(*args, **kwargs)
        else:
            to = f(*args, **kwargs)
            while True:
                if type(to) is GeneratorType:
                    stack.append(to)
                    to = next(to)
                else:
                    stack.pop()
                    if not stack:
                        break
                    to = stack[-1].send(to)
            return to

    return wrappedfunc


def add(i: int, v: int):
    x = i
    while i <= n:
        bit1[i] += v
        bit2[i] += (x - 1) * v
        i += lowBit[i]


def query(i: int):
    ans = 0
    x = i
    while i:
        ans += x * bit1[i] - bit2[i]
        i -= lowBit[i]
    return ans


def Update(l: int, r: int, x: int):
    add(l, x)
    add(r + 1, -x)


def Query(l: int, r: int):
    return query(r) - query(l - 1)


n, q = M()
val = [0] + read()
for i in range(1, n + 1):
    lowBit[i] = i & -i
for i in range(2, n + 1):
    LOG2[i] = LOG2[i >> 1] + 1
for _ in range(n - 1):
    u, v = M()
    child[u].append(v)
    child[v].append(u)


@bootstrap
def dfs(curr: int, parent: int):
    fa[curr][0] = parent
    deep[curr] = deep[parent] + 1
    global cnt
    cnt += 1
    dfn[cnt] = curr
    s[curr] = cnt
    for i in range(1, T + 1):
        fa[curr][i] = fa[fa[curr][i - 1]][i - 1]
    for nxt in child[curr]:
        if nxt != parent:
            yield dfs(nxt, curr)
    e[curr] = cnt
    yield


def lca(x: int, y: int):
    if deep[x] < deep[y]:
        x, y = y, x
    for i in range(T, -1, -1):
        if deep[fa[x][i]] >= deep[y]:
            x = fa[x][i]
    if x == y:
        return x
    for i in range(T, -1, -1):
        if fa[x][i] != fa[y][i]:
            x = fa[x][i]
            y = fa[y][i]
    return fa[x][0]


root = 1


def LCA(x, y):
    t1, t2, t3 = lca(root, x), lca(root, y), lca(x, y)
    mxDeep = max(deep[t1], deep[t2], deep[t3])
    if mxDeep == deep[t1]:
        return t1
    if mxDeep == deep[t2]:
        return t2
    return t3


def top(x: int, k: int):
    while k:
        step = LOG2[k]
        x = fa[x][step]
        k -= 1 << step
    return x


def Add(curr: int, v: int):
    if curr == root:
        Update(1, n, v)
    elif s[curr] <= s[root] and e[root] <= e[curr]:
        t = top(root, deep[root] - deep[curr] - 1)
        Update(1, n, v)
        Update(s[t], e[t], -v)
    else:
        Update(s[curr], e[curr], v)


def Ans(curr: int):
    if curr == root:
        return Query(1, n)
    elif s[curr] <= s[root] and e[root] <= e[curr]:
        t = top(root, deep[root] - deep[curr] - 1)
        return Query(1, n) - Query(s[t], e[t])
    return Query(s[curr], e[curr])


dfs(1, 0)
for i in range(1, n + 1):
    t = val[dfn[i]] - val[dfn[i - 1]]
    bit1[i] += t
    bit2[i] += (i - 1) * t
    j = i + lowBit[i]
    if j <= n:
        bit1[j] += bit1[i]
        bit2[j] += bit2[i]
for _ in range(q):
    op = read()
    if op[0] == 1:
        root = op[1]
    elif op[0] == 2:
        u, v, val = op[1:]
        Add(LCA(u, v), val)
    else:
        print(Ans(op[1]))

$$ 时间复杂度为: O((n+q)\log{n}) $$

解法二

参照朋友的博客的换根树剖。其实主要是讲讲 $top$ 咋求，就是一条路径上的倒数第二个点。

如果 $root$ 和 $lca$ 已经在同一条重链上了，显然直接返回 $lca$ 的重儿子 $son$。
不在同一条链让 $root$ 跳到 $lca$ 所在重链下面的一条重链的 $top$ 上。
基于第二天，答案要么为 $lca$ 的重儿子，要么即为下面一条重链的 $top$，主要看 $fa[root]=lca$，相同显然即为 $root$ (跳的结果)，否则为 $son$。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}


template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 1e5 + 10;
constexpr int T = 20;
int deep[N], son[N], siz[N], fa[N];
vector<int> child[N];
int n, q;

inline void dfs1(const int curr, const int parent)
{
    deep[curr] = deep[fa[curr] = parent] + 1;
    siz[curr] = 1;
    for (const auto nxt : child[curr])
    {
        if (nxt == parent)continue;
        dfs1(nxt, curr);
        siz[curr] += siz[nxt];
        if (siz[nxt] > siz[son[curr]])son[curr] = nxt;
    }
}

int idx[N], s[N], e[N], top[N], cnt;

inline void dfs2(const int curr, const int root)
{
    idx[++cnt] = curr, s[curr] = cnt, e[curr] = s[curr] + siz[curr] - 1;
    top[curr] = root;
    if (son[curr])dfs2(son[curr], root);
    for (const auto nxt : child[curr])if (nxt != fa[curr] and nxt != son[curr])dfs2(nxt, nxt);
}

int a[N], root = 1;

struct
{
    struct Node
    {
        ll sum, add, len;
    } node[N << 2];

#define len(x) node[x].len
#define add(x) node[x].add
#define sum(x) node[x].sum

    void Add(const int curr, const ll val)
    {
        add(curr) += val;
        sum(curr) += len(curr) * val;
    }

    void pushDown(const int curr)
    {
        if (add(curr))
        {
            Add(ls(curr),add(curr)), Add(rs(curr),add(curr));
            add(curr) = 0;
        }
    }

    void pushUp(const int curr)
    {
        sum(curr) = sum(ls(curr)) + sum(rs(curr));
    }

    void build(const int curr, const int l = 1, const int r = n)
    {
        len(curr) = r - l + 1;
        const int mid = l + r >> 1;
        if (l == r)
        {
            sum(curr) = a[idx[l]];
            return;
        }
        build(ls(curr), l, mid);
        build(rs(curr), mid + 1, r);
        pushUp(curr);
    }

    void Add(const int curr, const int l, const int r, const int val, const int s = 1, const int e = n)
    {
        if (l <= s and e <= r)
        {
            Add(curr, val);
            return;
        }
        const int mid = s + e >> 1;
        pushDown(curr);
        if (l <= mid)Add(ls(curr), l, r, val, s, mid);
        if (r > mid)Add(rs(curr), l, r, val, mid + 1, e);
        pushUp(curr);
    }

    ll Query(const int curr, const int l, const int r, const int s = 1, const int e = n)
    {
        if (l <= s and e <= r)return sum(curr);
        pushDown(curr);
        const int mid = s + e >> 1;
        ll ans = 0;
        if (l <= mid)ans += Query(ls(curr), l, r, s, mid);
        if (r > mid)ans += Query(rs(curr), l, r, mid + 1, e);
        return ans;
    }
} seg;

inline int lca(int x, int y)
{
    while (top[x] != top[y])
    {
        if (deep[top[x]] < deep[top[y]])swap(x, y);
        x = fa[top[x]];
    }
    if (deep[x] > deep[y])swap(x, y);
    return x;
}

inline int LCA(const int x, const int y)
{
    const int t1 = lca(root, x), t2 = lca(root, y), t3 = lca(x, y);
    const int maxDeep = max({deep[t1], deep[t2], deep[t3]});
    if (maxDeep == deep[t1])return t1;
    if (maxDeep == deep[t2])return t2;
    return t3;
}

//从root到curr的路径上最后一个点
inline int TreeTop(const int curr, int x = root)
{
    if (top[curr] == top[x])return son[curr];
    while (top[fa[top[x]]] != top[curr])x = fa[top[x]];
    x = top[x];
    if (fa[x] != curr)x = son[curr];
    return x;
}

inline bool sameTree(const int curr)
{
    return s[curr] <= s[root] and e[root] <= e[curr];
}

inline void Add(const int curr, const int val)
{
    if (curr == root)seg.Add(1, 1, n, val);
    else if (sameTree(curr))
    {
        const int del = TreeTop(curr);
        seg.Add(1, 1, n, val), seg.Add(1, s[del], e[del], -val);
    }
    else seg.Add(1, s[curr], e[curr], val);
}

inline ll Query(const int curr)
{
    if (curr == root)return seg.Query(1, 1, n);
    if (sameTree(curr))
    {
        const int del = TreeTop(curr);
        return seg.Query(1, 1, n) - seg.Query(1, s[del], e[del]);
    }
    return seg.Query(1, s[curr], e[curr]);
}

inline void solve()
{
    cin >> n >> q;
    forn(i, 1, n)cin >> a[i];
    forn(i, 1, n-1)
    {
        int u, v;
        cin >> u >> v;
        child[u].push_back(v), child[v].push_back(u);
    }
    dfs1(1, 0);
    dfs2(1, 1);
    seg.build(1);
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)cin >> root;
        else if (op == 2)
        {
            int u, v, val;
            cin >> u >> v >> val;
            Add(LCA(u, v), val);
        }
        else
        {
            int curr;
            cin >> curr;
            cout << Query(curr) << endl;
        }
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

Rust参照代码

#![allow(unused_variables)]
#![allow(clippy::large_stack_arrays)]
#![allow(unused_macros)]
#![allow(unused_mut)]
#![allow(dead_code)]
#![allow(unused_imports)]
#![allow(non_upper_case_globals)]

use std::io::{BufRead, Write};
use std::mem::swap;
use std::ops::{Add, AddAssign};

//----------------------------递归闭包---------------------------
struct Func<'a, A, F>(&'a dyn Fn(Func<'a, A, F>, A) -> F);

impl<'a, A, F> Clone for Func<'a, A, F> {
    fn clone(&self) -> Self {
        Self(self.0)
    }
}

impl<'a, A, F> Copy for Func<'a, A, F> {}

impl<'a, A, F> Func<'a, A, F> {
    fn call(&self, f: Func<'a, A, F>, x: A) -> F {
        (self.0)(f, x)
    }
}

fn y<A, R>(g: impl Fn(&dyn Fn(A) -> R, A) -> R) -> impl Fn(A) -> R {
    move |x| (|f: Func<A, R>, x| f.call(f, x))(Func(&|f, x| g(&|x| f.call(f, x), x)), x)
}

//Y组合子使用示例:(多参采用元组传参)
// let dfs = | f: & dyn Fn((usize, i32,bool)) -> bool, (i,sum,s): (usize,i32,bool) | -> bool{
//      if i == n {
//          return sum == 0 & & s;
//       }
//      return f((i + 1, sum + a[i], true)) | | f((i + 1, sum, s)) | |
// f((i + 1, sum - a[i], true));
// };
//----------------------------递归闭包---------------------------

//----------------------------常用函数----------------------------
#[inline]
fn prefix_array<T>(a: &Vec<T>, start: T) -> Vec<T>
where
    T: Add<Output = T> + Copy + AddAssign,
{
    (0..=a.len())
        .scan(start, |x, y| {
            if y == 0 {
                Some(start)
            } else {
                *x += a[y - 1];
                Some(*x)
            }
        })
        .collect::<Vec<T>>()
}

#[inline]
fn suffix_array<T>(a: &Vec<T>, end: T) -> Vec<T>
where
    T: Add<Output = T> + Copy + AddAssign,
{
    let mut tmp = (0..=a.len())
        .rev()
        .scan(end, |x, y| {
            if y == a.len() {
                Some(end)
            } else {
                *x += a[y];
                Some(*x)
            }
        })
        .collect::<Vec<T>>();
    tmp.reverse();
    tmp
}

//----------------------------常用函数----------------------------
macro_rules! __inner_io_prelude {
    ($scanner:ident, $out:ident, $dol:tt) =>
    {
        use crate::io::in_out;
        use crate::io::Scanner;
        use std::io::Write;
        let ($scanner, mut $out) = in_out();
        let mut $scanner = Scanner::new($scanner);
        macro_rules! __inner_input {(mut $a:ident : $type:tt) => {let mut $a: $type = $scanner.next();};($a:ident : $type:tt) => {let $a: $type = $scanner.next();};}
        macro_rules! input {($dol ($dol($idents: ident)+ : $type: tt),*) => {$dol (__inner_input!{$dol ($idents)+: $type})*};}
        macro_rules! put {($dol ($dol format:tt)*) => { let _ = write!($out, $dol ($dol format)*);};}
        macro_rules! puts {($dol ($dol format:tt)*) => { let _ = writeln!($out, $dol ($dol format)*);};}
        macro_rules! read_string_u8 {() => {$scanner.next::<String>().into_bytes()};}
        macro_rules! print_all {($A:expr) => {{for &v in &$A {let _ = write!($out, "{} ", v);}puts!();}};}
        macro_rules! read_usize {($n:expr) => {(0..$n).map(|_|$scanner.next::<usize>()).collect::<Vec<usize>>()};}
        macro_rules! read_i32 {($n:expr) => {(0..$n).map(|_|$scanner.next::<i32>()).collect::<Vec<i32>>()};}
        macro_rules! read_i64 {($n:expr) => {(0..$n).map(|_|$scanner.next::<i64>()).collect::<Vec<i64>>()};}
        macro_rules! read_i128 {($n:expr) => {(0..$n).map(|_|$scanner.next::<i128>()).collect::<Vec<i128>>()};}
        macro_rules! read_tow_array_usize {($n:expr,$m:expr) => {(0..$n).map(|_| read_usize!($m)).collect::<Vec<Vec<usize>>>()};}
        macro_rules! read_tow_array_i32 {($n:expr,$m:expr) => {(0..$n).map(|_| read_i32!($m)).collect::<Vec<Vec<i32>>>()};}
        macro_rules! read_tow_array_i64 {($n:expr,$m:expr) => {(0..$n).map(|_| read_i64!($m)).collect::<Vec<Vec<i64>>>()};}
        macro_rules! read_tow_array_i128 {($n:expr,$m:expr) => {(0..$n).map(|_| read_i128!($m)).collect::<Vec<Vec<i128>>>()};}
        macro_rules! count_bit {($n:expr) => {{let (mut ans, mut k) = (0_usize, $n);while k > 0 {ans += 1;k &= k - 1;}ans}};}
    };
}

macro_rules! io_prelude {
    ($scanner:ident, $out:ident) => { __inner_io_prelude!($scanner, $out, $); };
}

// --------------------------- tools -----------------------------------
mod io {
    use std::fs::File;
    use std::io::{stdin, stdout, BufRead, BufReader, BufWriter, Write};

    #[cfg(windows)]
    pub fn in_out() -> (impl BufRead, impl Write) {
        use std::os::windows::prelude::{AsRawHandle, FromRawHandle};
        unsafe {
            let stdin = File::from_raw_handle(stdin().as_raw_handle());
            let stdout = File::from_raw_handle(stdout().as_raw_handle());
            (BufReader::new(stdin), BufWriter::new(stdout))
        }
    }

    #[cfg(unix)]
    pub fn in_out() -> (impl BufRead, impl Write) {
        use std::os::unix::prelude::{AsRawFd, FromRawFd};
        unsafe {
            let stdin = File::from_raw_fd(stdin().as_raw_fd());
            let stdout = File::from_raw_fd(stdout().as_raw_fd());
            (BufReader::new(stdin), BufWriter::new(stdout))
        }
    }

    pub struct Scanner<R> {
        reader: R,
        buf_str: Vec<u8>,
        buf_iter: std::str::SplitAsciiWhitespace<'static>,
    }

    impl<R: BufRead> Scanner<R> {
        pub fn new(reader: R) -> Self {
            Self {
                reader,
                buf_str: Vec::new(),
                buf_iter: "".split_ascii_whitespace(),
            }
        }
        pub fn next<T: std::str::FromStr>(&mut self) -> T {
            loop {
                if let Some(token) = self.buf_iter.next() {
                    return token.parse().ok().expect("Failed parse");
                }
                unsafe {
                    self.buf_str.set_len(0);
                }
                self.reader
                    .read_until(b'\n', &mut self.buf_str)
                    .expect("Failed read");
                self.buf_iter = unsafe {
                    let slice = std::str::from_utf8_unchecked(&self.buf_str);
                    std::mem::transmute(slice.split_ascii_whitespace())
                }
            }
        }
    }
}

mod random {
    use std::time::SystemTime;

    const NN: usize = 312;
    const MM: usize = 156;
    const MATRIX_A: u64 = 0xB5026F5AA96619E9;
    const UM: u64 = 0xFFFFFFFF80000000;
    const LM: u64 = 0x7FFFFFFF;
    const F: u64 = 6364136223846793005;
    const MAG01: [u64; 2] = [0, MATRIX_A];

    pub struct Random {
        mt: [u64; NN],
        index: usize,
    }

    impl Random {
        pub fn new(seed: u64) -> Self {
            let mut res = Self {
                mt: [0u64; NN],
                index: NN,
            };
            res.mt[0] = seed;
            for i in 1..NN {
                res.mt[i] = F
                    .wrapping_mul(res.mt[i - 1] ^ (res.mt[i - 1] >> 62))
                    .wrapping_add(i as u64);
            }
            res
        }
        pub fn gen(&mut self) -> u64 {
            if self.index == NN {
                for i in 0..(NN - MM) {
                    let x = (self.mt[i] & UM) | (self.mt[i + 1] & LM);
                    self.mt[i] = self.mt[i + MM] ^ (x >> 1) ^ MAG01[(x & 1) as usize];
                }
                for i in (NN - MM)..(NN - 1) {
                    let x = (self.mt[i] & UM) | (self.mt[i + 1] & LM);
                    self.mt[i] = self.mt[i + MM - NN] ^ (x >> 1) ^ MAG01[(x & 1) as usize];
                }
                let x = (self.mt[NN - 1] & UM) | (self.mt[0] & LM);
                self.mt[NN - 1] = self.mt[MM - 1] ^ (x >> 1) ^ MAG01[(x & 1) as usize];
                self.index = 0;
            }
            let mut x = self.mt[self.index];
            self.index += 1;
            x ^= (x >> 29) & 0x5555555555555555;
            x ^= (x << 17) & 0x71D67FFFEDA60000;
            x ^= (x << 37) & 0xFFF7EEE000000000;
            x ^= x >> 43;
            x
        }
        pub fn next(&mut self, n: u64) -> u64 {
            self.gen() % n
        }
        pub fn next_bounds(&mut self, f: u64, t: u64) -> u64 {
            f + self.next(t - f + 1)
        }
    }

    static mut RAND: Option<Random> = None;

    pub fn random() -> &'static mut Random {
        unsafe {
            if RAND.is_none() {
                RAND = Some(Random::new(
                    (SystemTime::UNIX_EPOCH.elapsed().unwrap().as_nanos() & 0xFFFFFFFFFFFFFFFF)
                        as u64,
                ));
            }
            RAND.as_mut().unwrap()
        }
    }

    pub trait Shuffle {
        fn shuffle(&mut self);
    }

    impl<T> Shuffle for &mut [T] {
        fn shuffle(&mut self) {
            let len = self.len();
            for i in 0..len {
                let at = (random().gen() % ((i + 1) as u64)) as usize;
                self.swap(i, at);
            }
        }
    }
}

//----------------------------Test------------------------------常用板子书写区
#[inline]
pub fn lowBit(x: usize) -> usize {
    let y = x as i64;
    (y & -y) as usize
}

const N: usize = 100010;
static mut size: [usize; 100010] = [0; N];
static mut deep: [usize; 100010] = [0; N];
static mut son: [usize; 100010] = [0; N];
static mut fa: [usize; 100010] = [0; N];
static mut Root: usize = 1;

#[inline]
pub unsafe fn dfs1(edge: &Vec<Vec<usize>>, curr: usize, pa: usize) {
    deep[curr] = deep[pa] + 1;
    fa[curr] = pa;
    size[curr] = 1;
    for &nxt in &edge[curr] {
        if nxt == pa {
            continue;
        }
        dfs1(edge, nxt, curr);
        size[curr] += size[nxt];
        if size[nxt] > size[son[curr] as usize] {
            son[curr] = nxt;
        }
    }
}

static mut idx: [usize; 100010] = [0; N];
static mut top: [usize; 100010] = [0; N];
static mut s: [usize; 100010] = [0; N];
static mut e: [usize; 100010] = [0; N];
static mut val: [i64; 100010] = [0; N];
static mut cnt: usize = 0;

#[inline]
pub unsafe fn dfs2(edge: &Vec<Vec<usize>>, curr: usize, root: usize) {
    cnt += 1;
    idx[cnt] = curr;
    s[curr] = cnt;
    e[curr] = cnt + size[curr] - 1;
    top[curr] = root;
    if son[curr] != 0 {
        dfs2(edge, son[curr], root);
    }
    for &nxt in &edge[curr] {
        if nxt != fa[curr] && nxt != son[curr] {
            dfs2(edge, nxt, nxt);
        }
    }
}

static mut bit1: [i64; 100010] = [0; N];
static mut bit2: [i64; 100010] = [0; N];

#[inline]
pub unsafe fn add(mut i: usize, n: usize, v: i64) {
    let x = i as i64;
    while i <= n {
        bit1[i] += v;
        bit2[i] += (x - 1) * v;
        i += lowBit(i);
    }
}

#[inline]
pub unsafe fn Add(l: usize, r: usize, n: usize, v: i64) {
    add(l, n, v);
    add(r + 1, n, -v);
}

#[inline]
pub unsafe fn query(mut i: usize) -> i64 {
    let mut ans = 0;
    let mut x = i as i64;
    while i != 0 {
        ans += bit1[i] * x - bit2[i];
        i -= lowBit(i);
    }
    ans
}

#[inline]
pub unsafe fn Query(l: usize, r: usize) -> i64 {
    query(r) - query(l - 1)
}

#[inline]
pub unsafe fn lca(mut x: usize, mut y: usize) -> usize {
    while top[x] != top[y] {
        if deep[top[x]] < deep[top[y]] {
            swap(&mut x, &mut y);
        }
        x = fa[top[x]];
    }
    if deep[x] > deep[y] {
        swap(&mut x, &mut y);
    }
    x
}

#[inline]
pub unsafe fn LCA(x: usize, y: usize) -> usize {
    let t1 = lca(x, Root);
    let t2 = lca(y, Root);
    let t3 = lca(x, y);
    let mxDeep = deep[t1].max(deep[t2]).max(deep[t3]);
    if mxDeep == deep[t1] {
        return t1;
    }
    if mxDeep == deep[t2] {
        return t2;
    }
    t3
}

#[inline]
pub unsafe fn TreeTop(mut curr: usize) -> usize {
    if top[curr] == top[Root] {
        return son[curr];
    }
    let mut x = Root;
    while top[fa[top[x]]] != top[curr] {
        x = fa[top[x]];
    }
    x = top[x];
    if fa[x] != curr {
        x = son[curr];
    }
    x
}

#[inline]
pub unsafe fn isSame(curr: usize) -> bool {
    s[curr] <= s[Root] && e[Root] <= e[curr]
}

#[inline]
pub unsafe fn Update(curr: usize, n: usize, v: i64) {
    if curr == Root {
        Add(1, n, n, v);
    } else if isSame(curr) {
        let del = TreeTop(curr);
        Add(1, n, n, v);
        Add(s[del], e[del], n, -v);
    } else {
        Add(s[curr], e[curr], n, v);
    }
}

#[inline]
pub unsafe fn Ans(curr: usize, n: usize) -> i64 {
    return if curr == Root {
        Query(1, n)
    } else if isSame(curr) {
        let del = TreeTop(curr);
        Query(1, n) - Query(s[del], e[del])
    } else {
        Query(s[curr], e[curr])
    };
}
//----------------------------Test------------------------------常用板子书写区
//-----------------------------main-------------------------------------主逻辑书写区

#[inline]
pub unsafe fn solve() {
    io_prelude!(scanner, out);
    //-----------------------------------------------------------------
    input! {n:usize,q:usize}
    let mut edge: Vec<Vec<usize>> = vec![vec![]; n + 1];
    for i in 1..=n {
        val[i] = scanner.next::<i64>();
    }
    for _ in 0..n - 1 {
        input! {u:usize,v:usize}
        edge[u].push(v);
        edge[v].push(u);
    }
    dfs1(&edge, 1, 0);
    dfs2(&edge, 1, 1);
    for i in 1..=n {
        let t = val[idx[i]] - val[idx[i - 1]];
        bit1[i] += t;
        bit2[i] += (i as i64 - 1) * t;
        let j = i + lowBit(i);
        if j <= n {
            bit1[j] += bit1[i];
            bit2[j] += bit2[i];
        }
    }
    for _ in 0..q {
        input! {op:usize}
        if op == 1 {
            Root = scanner.next::<usize>();
        } else if op == 2 {
            input! {u:usize,v:usize,t:i64}
            Update(LCA(u, v), n, t);
        } else {
            input! {curr:usize}
            puts!("{}", Ans(curr, n));
        }
    }
}

//-----------------------------main-------------------------------------主逻辑书写区
fn main() {
    unsafe {
        solve();
    }
}

$$ 不涉及跳链修改与查询，只有子树操作，时间复杂度为:\ O((n+q)\log{n}) $$

如果要用 $LCT$ 做子树操作是较为困难的，当然也能做，具体的每个点同时维护虚子树信息，但这些信息不能单纯地使用懒标记维护，需要维护一个标记永久化的虚子树全局加标记，在虚实变化时通过这个标记来更新真实的虚实子树和总信息，细节较多，后续写了再补代码。当然 $ETT$ 和 $Top Tree$ 应该也是完全能做的。

posted @ 2024-02-23 17:36 Athanasy 阅读(28) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Athanasy

CF916E Jamie and Tree 题解

题目链接：CF 或者 洛谷

本题难点在于换根 LCA 与换根以后的子树范围寻找，重点讲解

解法一

解法二

公告

题目链接：CF 或者洛谷