P4559 [JSOI2018] 列队 题解

题目链接：列队

半年前 mark 的题，结果现在一下子就会做了。顺便写写我的手玩过程和复杂度说明。

考虑比较特殊的情况：

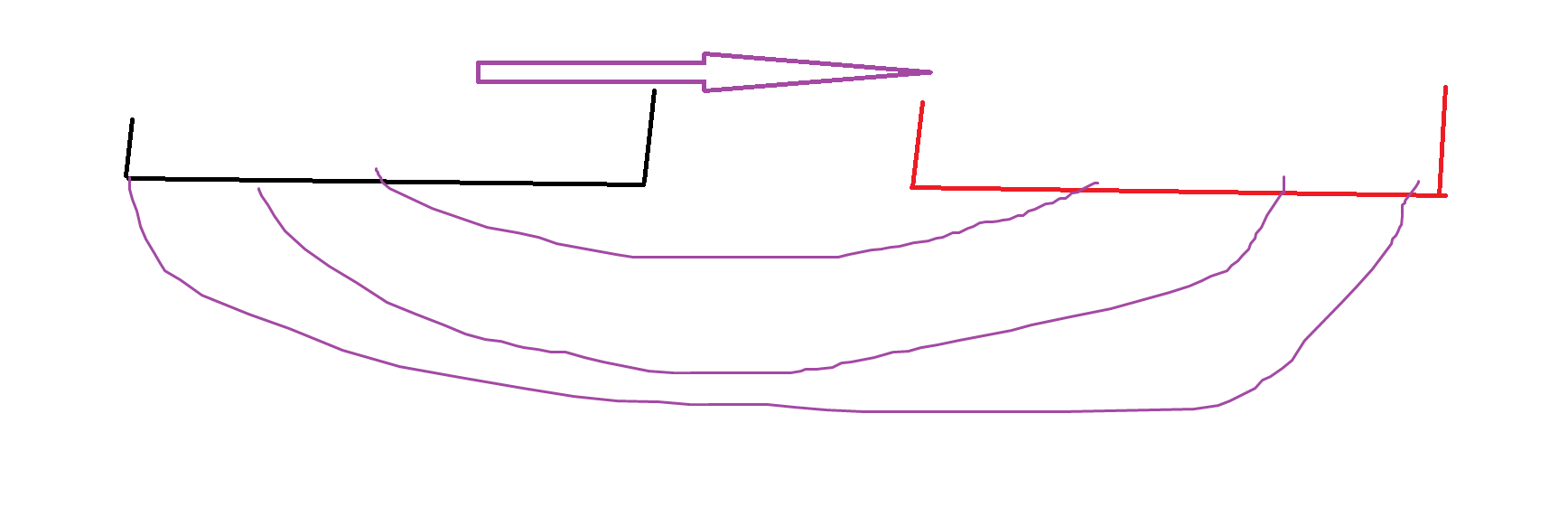
比较特殊的，发现从黑色到红色区间我们无论咋选择，由于 \(\left| a_{right}-a_{left}\right|\)，这玩意如果 \(right\) 表示红色的一边，那么这个绝对值可以直接拆掉，那么其实最后就是 \(sum(right)-sum(left)\)。跟你咋连无关。然后其实一开始我就猜到了应该是跟可持久化线段树有关的，因为询问涉及到哦一个区间上的 “无序子数组”，这玩意一点性质都没有，然后观察去掉绝对值的方式一定和有序有关，所以如果你看到这题猜不到可能用可持久化线段树化为有序问题就得加练这一块了。

其实难点还是询问区间和目标区间有交叉，其实这个题能猜结论也只能往有序对一一对应去猜，除此之外我猜不到别的结论了，注意到目标区间是连续得到，我们随便挑一组相邻交叉看。

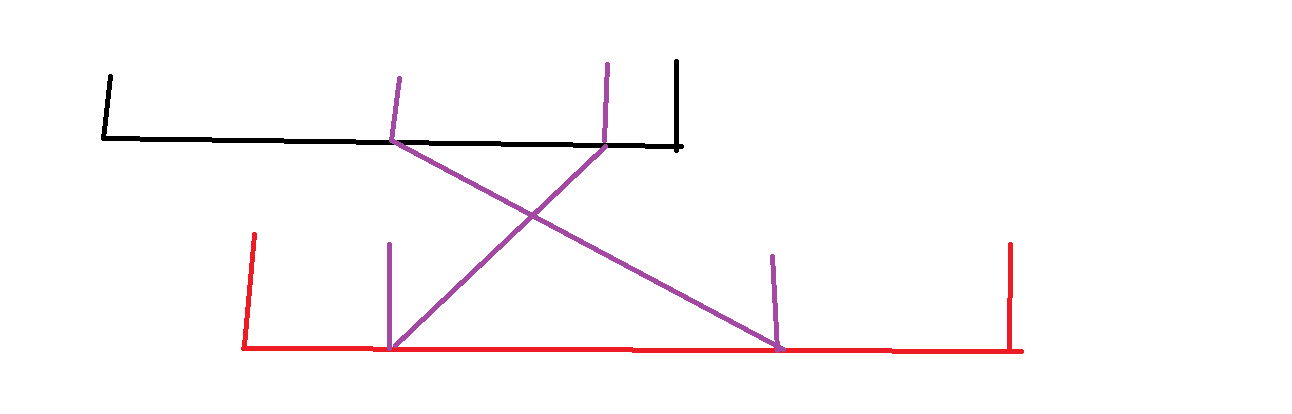
如果我们不按顺序对一一对应去选，就会出现图上这种交叉，就图上这个情况，很显然多了一段交叉的更远距离。

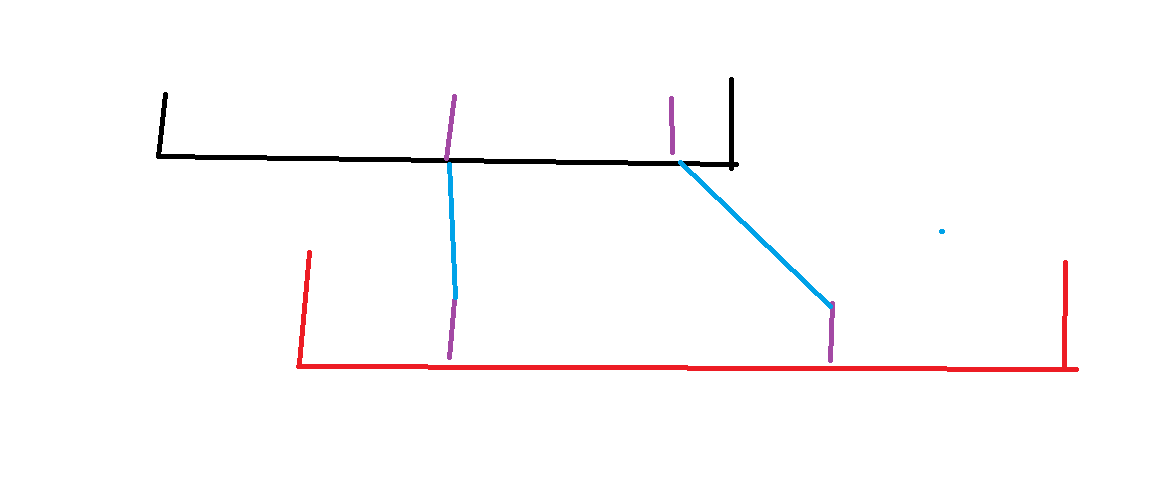
其实这玩意应该算一个很经典的问题吧，一般用邻项交换法就能证明，最小化曼哈顿距离也是用差不多的分析方法。保证相对顺序对就是最小化两个数组的差异程度。

现在难点在于统计，很显然一定有某个分割点 \(split\) 使得在它之前都有 \(a_{right} \ge a_{left}\)，在它之后则为 \(a_{left} \ge a_{rigth}\)，因为我们查询区间是连续的，所以当出现 \(a_{left} \ge a_{split}\) 的时候，\(split\) 后的点只会比上一个点 \(+1\)，而 \(a_{left}\) 则是至少 \(+1\)。那其实问题很好办了，如果一个值域上的 \(mid\) 直接满足了分割点的需求，求可以直接累计上这个值域上的所有贡献，具体的是 \(right-left\) 还是 \(left-right\) 取决于它在分割点左边还是右边，二分分割点的位置也很简单，知道值域里有多少个数，则 \(qeuryL+leftSize-1\) 即为分割点，然后和 \(mid\) 一比较就 \(ok\) 了，而可持久化线段树上树上二分找出这个分割点的复杂度显然是 \(log\) 级别。连续段求和，显然就是等差数列求和了，另一边贡献就直接基础树上前缀和作差查找。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}


template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 5e5 + 10;
constexpr int MX = 2e6;

struct Node
{
    int left, right, cnt;
    ll sum;
} node[N << 5];

#define left(x) node[x].left
#define right(x) node[x].right
#define cnt(x) node[x].cnt
#define sum(x) node[x].sum
int cnt, n;

inline void add(const int pre, int& curr, const int val, const int l = 1, const int r = MX)
{
    node[curr = ++cnt] = node[pre];
    cnt(curr)++, sum(curr) += val;;
    const int mid = l + r >> 1;
    if (l == r)return;
    if (val <= mid)add(left(pre),left(curr), val, l, mid);
    else add(right(pre),right(curr), val, mid + 1, r);
}

//等差数列求和公式
inline ll getDiff(const ll start, const ll end)
{
    return (start + end) * (end - start + 1) / 2;
}

inline ll query(const int L, const int R, const int l, const int r, const int s = 1, const int e = MX)
{
    ll ans = 0;
    const int leftSize = cnt(left(R)) - cnt(left(L));
    const int rightSize = cnt(right(R)) - cnt(right(L));
    const int mid = s + e >> 1;
    if (leftSize)
    {
        //分割区间[l,l+leftSize-1]
        if (mid <= l + leftSize - 1)ans += getDiff(l, l + leftSize - 1) - (sum(left(R)) - sum(left(L)));
        else ans += query(left(L),left(R), l, l + leftSize - 1, s, mid);
    }
    if (rightSize)
    {
        //分割区间[l+leftSize,r]
        if (l + leftSize <= mid + 1)ans += sum(right(R)) - sum(right(L)) - getDiff(l + leftSize, r);
        else ans += query(right(L),right(R), l + leftSize, r, mid + 1, e);
    }
    return ans;
}

int q, x;
int root[N];

inline void solve()
{
    cin >> n >> q;
    forn(i, 1, n)
    {
        cin >> x;
        add(root[i - 1], root[i], x);
    }
    while (q--)
    {
        int l, r, k;
        cin >> l >> r >> k;
        cout << query(root[l - 1], root[r], k, k + r - l) << endl;
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[时间复杂度为:\ O((n+q)\log{MX}) \]