CF526F Pudding Monsters 题解

合集 - codeforces题解集1(37)

1.CF1916E Happy Life in University 题解2023-12-312.CF763E Timofey and our friends animals题解2024-01-033.CF1270G Subset with Zero Sum2024-01-054.CF1045G AI robots题解2024-01-055.CF940F Machine Learning题解2024-01-066.CF678F Lena and Queries题解2024-01-127.CF1921F Sum of Progression 题解2024-01-16

8.CF526F Pudding Monsters 题解2024-01-21

9.CF455D Serega and Fun 题解2024-01-2210.CF351D Jeff and Removing Periods 题解2024-01-2211.CF452F Permutation 与 P2757 [国家集训队] 等差子序列 题解2024-01-2312.CF911G Mass Change Queries 题解2024-01-2413.CF145E Lucky Queries 题解2024-01-2514.CF1515F Phoenix and Earthquake 题解2024-01-2615.CF765F Souvenirs 题解2024-01-2716.CF1764H Doremy's Paint 2 题解2024-01-2917.CF1000F One Occurrence题解2024-01-3018.CF813E Army Creation 题解2024-01-3119.CF1706E Qpwoeirut and Vertices 题解2024-02-0120.CF620E New Year Tree 题解2024-02-0221.CF1454F Array Partition 题解2024-02-0322.CF1771F Hossam and Range Minimum Query 题解2024-02-0823.CF1931F Chat Screenshots 另一种题解2024-02-1424.CF896C Willem, Chtholly and Seniorious 题解2024-02-1525.CF55D Beautiful numbers 题解2024-02-1626.CF916E Jamie and Tree 题解2024-02-2327.CF696B Puzzles 题解2024-02-2828.CF383C Propagating tree 题解2024-02-2929.CF1436E Complicated Computations 题解2024-03-0830.CF817F MEX Queries 题解2024-03-2031.CF1638E Colorful Operations 题解2024-03-2132.CF1618G Trader Problem 题解2024-03-2233.CF794F Leha and security system 题解2024-03-2334.CF371E Subway Innovation 题解2024-04-0435.CF1200E Compress Words 题解2024-04-0636.CF1884D Counting Rhyme 题解2024-05-1737.CF1982F Sorting Problem Again 题解2024-06-26

收起

题目链接：CF 或者 洛谷

析合树真是连续段问题的降智神器

先看下题目的一些特殊性，每行每列恰好有一个棋子。考虑特殊性，$n\times n$ 的棋盘，那么就该判断是否有 $n$ 个棋子，容易观察到，也就是相当于每一行并且每一列都有一个棋子。而容易知道，这些棋子所在的行或者列拿出来应当是“连续的”。

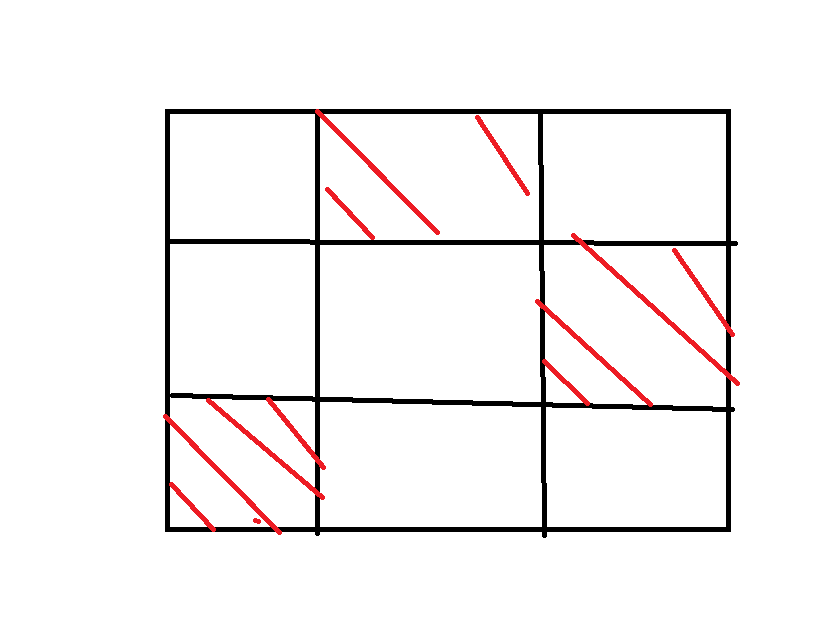
容易知道一个事实，如果你的行是连续的，并且列是连续的，那么一定能够组成答案，但如果只满足其中一个，就不一定了：

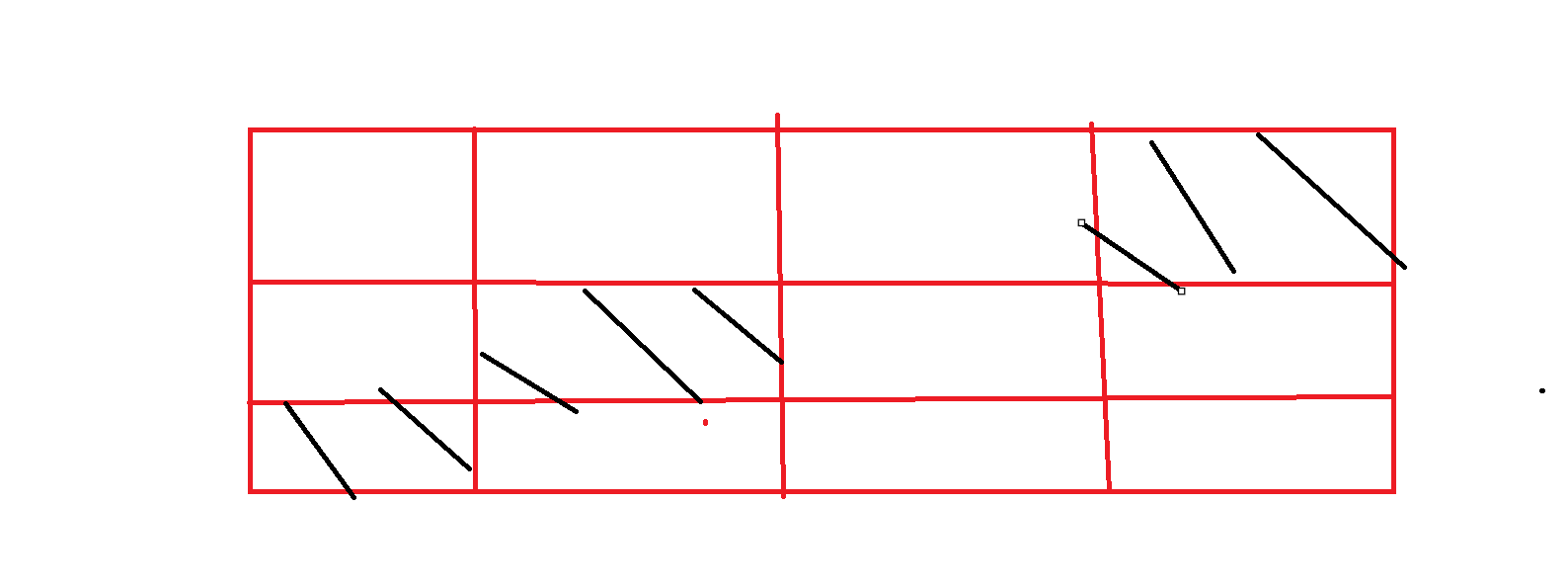
比如如图所示，这三个黑色格子是属于行连续的，但列并不连续，而它们并不能组成答案。同理，列连续但行不连续也无法组成答案。

我们得到了本题的一个贡献的充要条件，行需要连续，列也需要连续，但这个二维问题比较难以解决，我们考虑让某一维先连续，即比如以行为关键字进行排序，这样一来任意一段都是行连续了，这个时候在来考虑列连续性即可。当然了也可以这样去写：$idx[row]=col$，这样一来，自然按照行排好序了，因为这本质是排列，并不会出现重复数字，也是排列问题常用的一种排序方式。

接下来就转变为了一个数组上，有多少个连续段区间的问题，线段树确实处理起来比较需要思维难度，但析合树解决起来就不需要太多思考。

1. 如果某个点是析点，显然贡献为 $1$，只有它的所有儿子节点合并起来才是连续段。

2. 如果某个点是合点，显然贡献为 $(\genfrac{}{}{0ex}{}{siz}{2})$，因为它的任意两个儿子节点都可以组成一个新的连续段，所以应该为任取两个儿子的方案数。

那么只需要建析合树，然后遍历一遍树节点就行了。

参照代码

#include <bits/stdc++.h>
 
// #pragma GCC optimize("Ofast,unroll-loops")
// #pragma GCC optimize(2)
 
// #define isPbdsFile
 
#ifdef isPbdsFile
 
#include <bits/extc++.h>
 
#else
 
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
 
#endif
 
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
 
template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}
 
template <typename T>
T lowBit(T x)
{
    return x & -x;
}
 
template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}
 
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}
 
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}
 
template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}
 
template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}
 
template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}
 
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}
 
 
template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;
 
    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }
 
    T3() { one = tow = three = 0; }
 
    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};
 
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}
 
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}
 
constexpr int N = 6e5 + 10;
constexpr int T = 25;
int idx[N];
int n;
 
struct
{
    int MAX[N][T], MIN[N][T];
    int LOG2[N];
 
    void build()
    {
        forn(i, 2, n)LOG2[i] = LOG2[i >> 1] + 1;
        const int k = LOG2[n] + 1;
        forn(i, 1, n)MAX[i][0] = MIN[i][0] = idx[i];
        forn(j, 1, k)
        {
            forn(i, 1, n-(1<<j)+1)
            {
                MAX[i][j] = max(MAX[i][j - 1], MAX[i + (1 << j - 1)][j - 1]);
                MIN[i][j] = min(MIN[i][j - 1], MIN[i + (1 << j - 1)][j - 1]);
            }
        }
    }
 
    int query(const int l, const int r) const
    {
        const int k = LOG2[r - l + 1];
        return max(MAX[l][k], MAX[r - (1 << k) + 1][k]) - min(MIN[l][k], MIN[r - (1 << k) + 1][k]);
    }
} ST;
 
struct
{
    struct Node
    {
        int Min, Add;
    } node[N << 2];
 
#define Min(x) node[x].Min
#define Add(x) node[x].Add
 
    void push_up(const int curr)
    {
        Min(curr) = min(Min(ls(curr)),Min(rs(curr)));
    }
 
    void push_down(const int curr)
    {
        if (Add(curr))
        {
            Min(ls(curr)) += Add(curr), Min(rs(curr)) += Add(curr);
            Add(ls(curr)) += Add(curr), Add(rs(curr)) += Add(curr);
            Add(curr) = 0;
        }
    }
 
    void add(const int curr, const int l, const int r, const int val, const int s = 1, const int e = n)
    {
        if (l <= s and e <= r)
        {
            Min(curr) += val, Add(curr) += val;
            return;
        }
        const int mid = s + e >> 1;
        push_down(curr);
        if (l <= mid)add(ls(curr), l, r, val, s, mid);
        if (r > mid)add(rs(curr), l, r, val, mid + 1, e);
        push_up(curr);
    }
 
    int query(const int curr = 1, const int l = 1, const int r = n)
    {
        if (l == r)return l;
        const int mid = l + r >> 1;
        push_down(curr);
        if (!Min(ls(curr)))return query(ls(curr), l, mid);
        return query(rs(curr), mid + 1, r);
    }
} Seg;
 
struct DCT
{
    int left, right, type, rightL;
 
    DCT(const int left, const int right, const int type = 0, const int right_l = 0)
        : left(left),
          right(right),
          type(type),
          rightL(right_l)
    {
    }
 
    DCT() = default;
} dct[N];
 
inline bool isContinue(const int l, const int r)
{
    return ST.query(l, r) == r - l;
}
 
#define left(x) dct[x].left
#define right(x) dct[x].right
#define type(x) dct[x].type
#define rightL(x) dct[x].rightL
int cnt;
int stMax[N], stMin[N], maxCnt, minCnt;
#define maxTop idx[stMax[maxCnt]]
#define minTop idx[stMin[minCnt]]
int node[N];
vector<int> child[N];
stack<int> st;
#define root st.top()
int dctRoot;
 
inline void build()
{
    forn(i, 1, n)
    {
        while (maxCnt and idx[i] >= maxTop)Seg.add(1, stMax[maxCnt - 1] + 1, stMax[maxCnt], -maxTop), --maxCnt;
        while (minCnt and idx[i] <= minTop)Seg.add(1, stMin[minCnt - 1] + 1, stMin[minCnt],minTop), --minCnt;
        Seg.add(1, stMax[maxCnt] + 1, i, idx[i]), Seg.add(1, stMin[minCnt] + 1, i, -idx[i]);
        stMax[++maxCnt] = stMin[++minCnt] = i;
        int curr;
        dct[curr = node[i] = ++cnt] = DCT(i, i);
        const int L = Seg.query();
        while (!st.empty() and left(root) >= L)
        {
            if (type(root) and isContinue(rightL(root), i))
            {
                right(root) = i, rightL(root) = left(curr);
                child[root].push_back(curr);
                curr = root;
                st.pop();
            }
            else if (isContinue(left(root), i))
            {
                dct[++cnt] = DCT(left(root), i, 1,left(curr));
                child[cnt].push_back(root), child[cnt].push_back(curr);
                curr = cnt;
                st.pop();
            }
            else
            {
                child[++cnt].push_back(curr);
                do child[cnt].push_back(root), st.pop();
                while (!isContinue(left(root), i));
                dct[cnt] = DCT(left(root), i);
                child[cnt].push_back(root);
                curr = cnt;
                st.pop();
            }
        }
        st.push(curr);
        Seg.add(1, 1, i, -1);
    }
    dctRoot = root;
}
 
ll ans;
 
inline void dfs(const int curr)
{
    ll siz = child[curr].size();
    if (type(curr))ans += siz * (siz - 1) / 2;
    else ans++;
    for (const auto nxt : child[curr])dfs(nxt);
}
 
inline void solve()
{
    cin >> n;
    forn(i, 1, n)
    {
        int x, y;
        cin >> x >> y;
        idx[x] = y;
    }
    ST.build();
    build();
    dfs(dctRoot);
    cout << ans;
}
 
signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}
 

$$\mathrm{时}\mathrm{间}\mathrm{复}\mathrm{杂}\mathrm{度}\mathrm{为}O(n\log n)$$