ABC311_g One More Grid Task 题解
题目链接:Atcoder 或者 洛谷
对于解决二维区间内的最值类型问题,我们常常有一类特别好用的方法,就是悬线法,它可以看做是单调栈的子集,但更加好理解和书写。
对于悬线法,我们有一个常见的模型,找出面积最大的符合题意的最大的矩形:
例题 P4147 玉蟾宫。对于悬线法而言,我们需要理解什么是悬线:
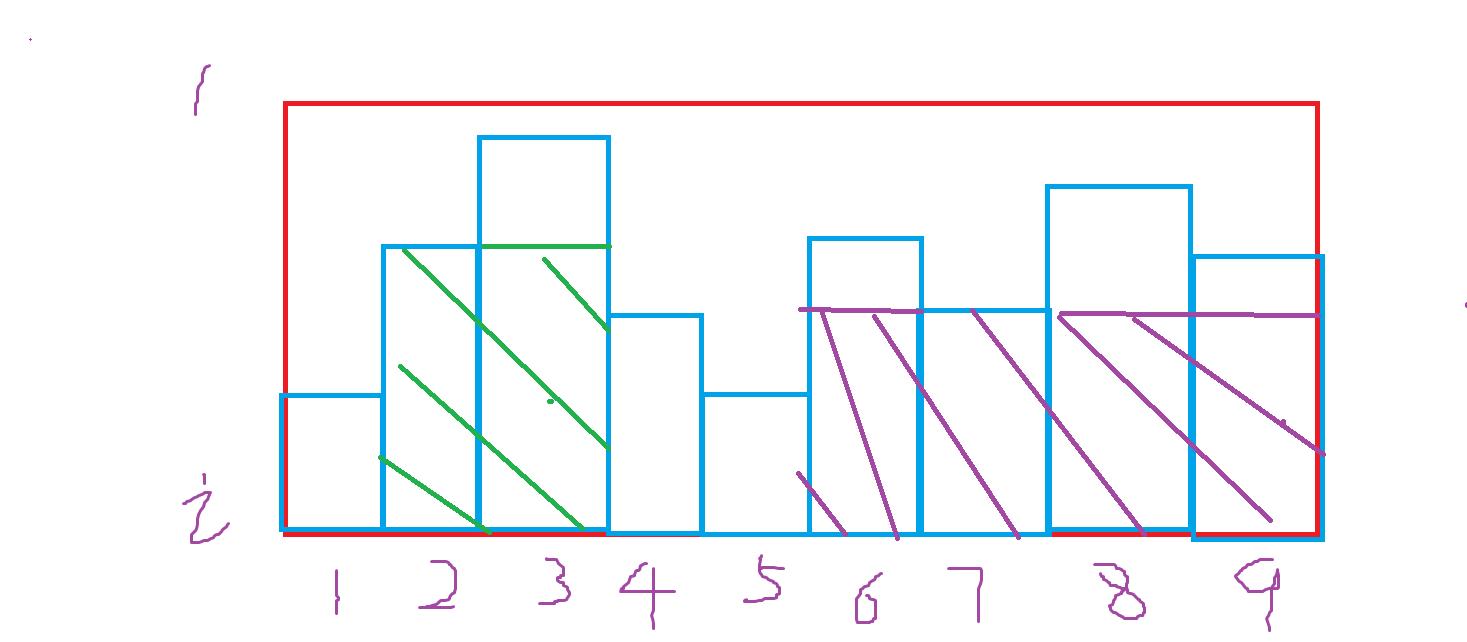
如图所示,我们可以很容易的从第 \(1\) 行往第 \(i\) 行更新的同时,维护从当前行往上满足的最长悬线,在例题当中,则为从当前位置往上的最长连续是 \(F\) 的段。对于以 \(2\) 号位置的上悬线作为高的最优矩形,我们显然要找到它的左右悬线,如图所示,如果它左右两边的上悬线比它高,显然就能拓展出去,使得当前的这根悬线高度不会变小。绿色图形则为最终悬线更新结果。而对于 \(7\) 号上悬线而言,紫色图形则为最终结果。而左右悬线是很好维护求出来的,只需要保证上悬线不减即可,其实这个思想就是类似单调栈思想了,找到左右最先小于自身的端点,但单调栈书写这个逻辑要略显复杂一丢丢,在弹栈时去判断,我们可以用一种更为简单的方法:
更新左右悬线参照代码
forn(j, 1, m)while (L[j] > 1 and h[L[j] - 1] >= h[j])L[j] = L[L[j] - 1];
forv(j, m, 1)while (R[j] < m and h[R[j] + 1] >= h[j])R[j] = R[R[j] + 1];
从左往右更新左悬线,如果比上一个左悬线对应的上悬线还小,那就可以继续拓展到上一个左悬线可以拓展到的左悬线,右悬线就倒序遍历,同理。建议将本题反复练熟再回到原问题上。
至此,回到原题,考虑如何将本题转化为基本的悬线法模型:
很显然的是,本地比较难以处理的是这个区间最小值如何处理,我们注意到区间最小值的数量不超过 \(N\),而 \(N\) 仅仅为 \(300\),所以我们可以考虑枚举最小值是多少,那么这样一来,每个点对最小值而言只有两种情况:
-
如果 \(a[i][j] \ge Value_{min}\),那么很显然对应的其实就是例题的 \(==F\)。
-
如果 \(a[i][j] < Value_{min}\),很显然就是对应的 \(==R\)。
问题转变为原例题问题,找到最大的全为 \(F\) 的矩形,然后答案为这个矩形内的数之和乘上我们枚举的最小值。而求区间和问题,可以预处理出前缀和解决。所以问题至此解决。
参照代码
#include <bits/stdc++.h>
// #pragma GCC optimize("Ofast,unroll-loops")
// #pragma GCC optimize(2)
#define isPbdsFile
#ifdef isPbdsFile
#include <bits/extc++.h>
#else
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
#endif
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
template <typename T>
int disc(T* a, int n)
{
return unique(a + 1, a + n + 1) - (a + 1);
}
template <typename T>
T lowBit(T x)
{
return x & -x;
}
template <typename T>
T Rand(T l, T r)
{
static mt19937 Rand(time(nullptr));
uniform_int_distribution<T> dis(l, r);
return dis(Rand);
}
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
return (a % b + b) % b;
}
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
a %= c;
T1 ans = 1;
for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
return modt(ans, c);
}
template <typename T>
void read(T& x)
{
x = 0;
T sign = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')sign = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
x *= sign;
}
template <typename T, typename... U>
void read(T& x, U&... y)
{
read(x);
read(y...);
}
template <typename T>
void write(T x)
{
if (typeid(x) == typeid(char))return;
if (x < 0)x = -x, putchar('-');
if (x > 9)write(x / 10);
putchar(x % 10 ^ 48);
}
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
write(x), putchar(c);
write(c, y...);
}
template <typename T11, typename T22, typename T33>
struct T3
{
T11 one;
T22 tow;
T33 three;
bool operator<(const T3 other) const
{
if (one == other.one)
{
if (tow == other.tow)return three < other.three;
return tow < other.tow;
}
return one < other.one;
}
T3() { one = tow = three = 0; }
T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
{
}
};
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
if (x < y)x = y;
}
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
if (x > y)x = y;
}
constexpr int N = 310;
ll pre[N][N];
int h[N], L[N], R[N];//上悬线的长度,左右悬线的位置
//二维前缀和求区间和
inline ll query(const int x1, const int y1, const int x2, const int y2)
{
return pre[x2][y2] - pre[x1 - 1][y2] - pre[x2][y1 - 1] + pre[x1 - 1][y1 - 1];
}
int n, m;
ll ans;
int a[N][N];
//悬线法解决最小值为val的答案
inline ll getAns(const ll val)
{
ll res = 0;
fill_n(h + 1, m, 0); //每个点上悬线长度初始化为0
forn(i, 1, n)
{
forn(j, 1, m)
{
if (a[i][j] >= val)h[j]++;//符合扩展条件,上悬线长度增加
else h[j] = 0;//不符合扩展条件,没有上悬线
L[j] = R[j] = j;//初始化当前列的左右悬线
}
forn(j, 1, m)while (L[j] > 1 and h[L[j] - 1] >= h[j])L[j] = L[L[j] - 1];
forv(j, m, 1)while (R[j] < m and h[R[j] + 1] >= h[j])R[j] = R[R[j] + 1];
forn(j, 1, m)if (h[j])uMax(res, query(i - h[j] + 1, L[j], i, R[j]) * val);//有上悬线就计算答案
}
return res;
}
int mx;
inline void solve()
{
cin >> n >> m;
forn(i, 1, n)
{
forn(j, 1, m)
{
cin >> a[i][j];
uMax(mx, a[i][j]), pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + a[i][j];
}
}
forn(i, 1, mx)uMax(ans, getAns(i));//枚举最小值
cout << ans;
}
signed int main()
{
// MyFile
Spider
//------------------------------------------------------
// clock_t start = clock();
int test = 1;
// read(test);
// cin >> test;
forn(i, 1, test)solve();
// while (cin >> n, n)solve();
// while (cin >> test)solve();
// clock_t end = clock();
// cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}
总结:
关于悬线法而言,它常常会与二维区间的最优矩形查找有关。而我们实际上需要转化为普通悬线法的模型,需要优先考虑上悬线的扩展条件,对于某一个点而言,如果它的上悬线的扩展条件固定了,那么左右条件悬线扩展就很轻松了。建议反复将例题进行熟悉,这样遇到其他的其他的题型也可以转化为最本质的模型去解决。



