P4149 [IOI2011] Race 题解
题目链接:Race
点分治基本题,从这题简单阐述点分治如何思考问题的。点分治常见的解决一类问题,就是树里面的一些路径类问题。比如一些计数是最常见的。
点分治的一个核心计数思想:

如图所见,对于某个点而言,我们将它作为根,那么它的子树并排地排起来,我们依次遍历每棵树并累计树。

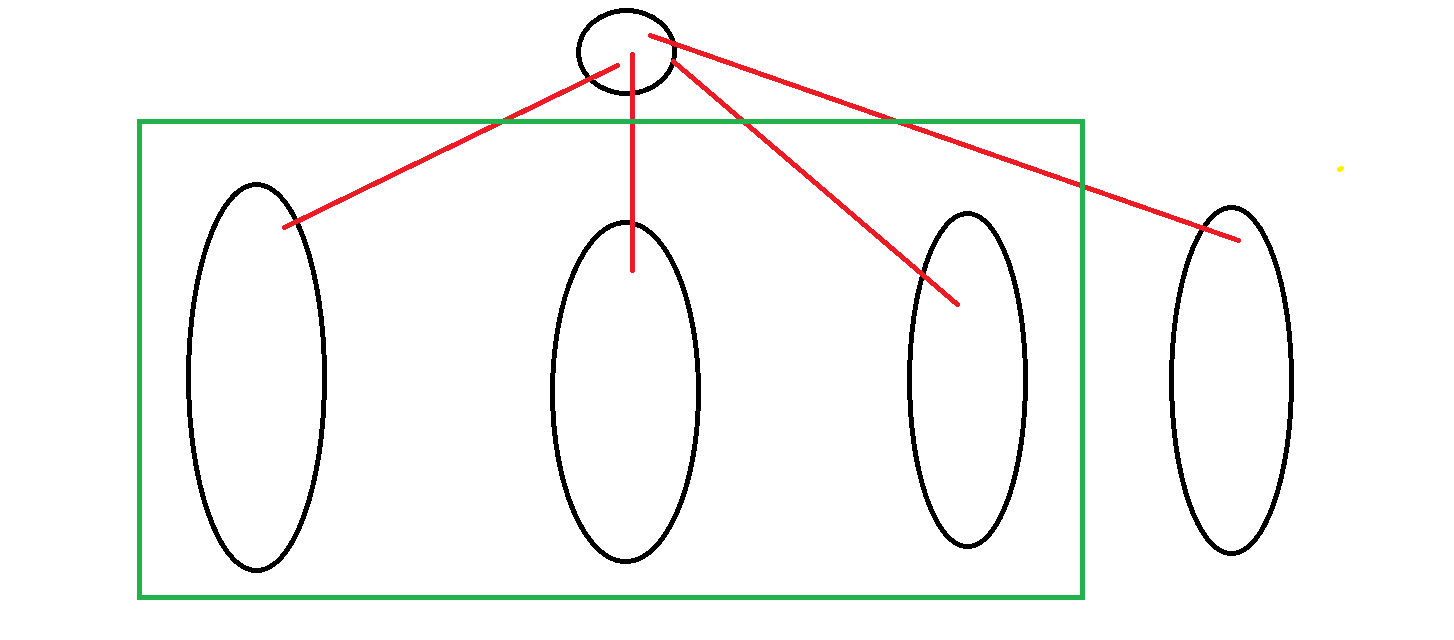
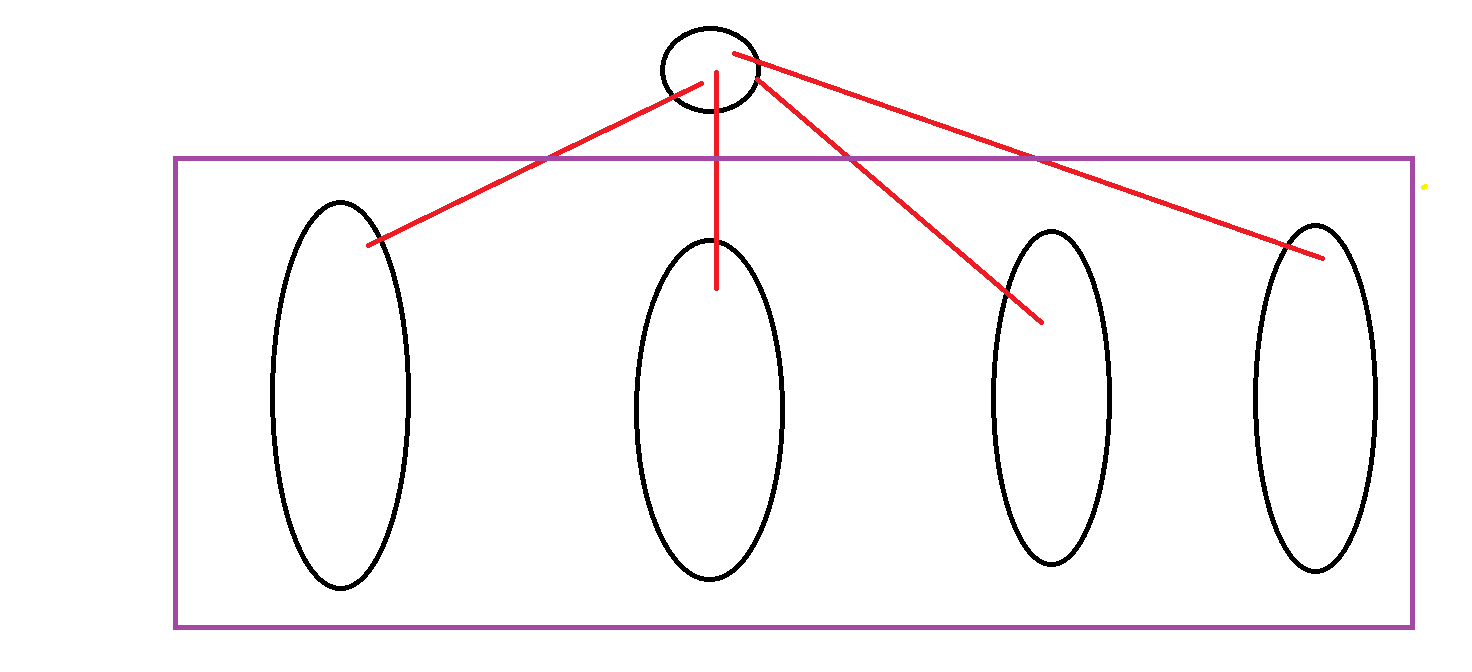
我们容易知道,包括这个点的路径分为两类:
-
只会存在于某个子树中
-
由两个子树类路径拼接而成
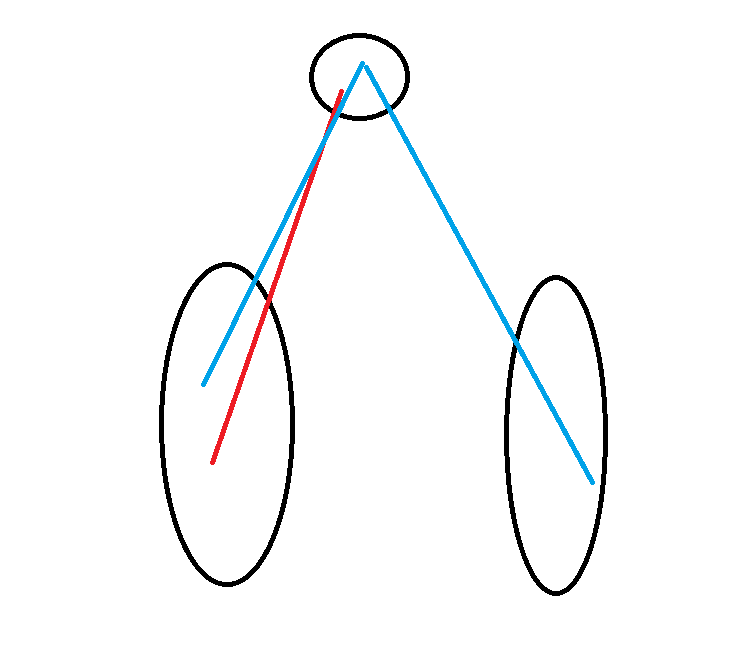
红色为只经过一棵子树的路径,蓝色为两条拼接在一起。很显然的是,我们很容易在遍历的时候维护前缀和路径长以及它的边数量,那么对于同一棵子树里面的路径,我们可以增加一个路径长为 \(0\),边数为 \(0\) 的前缀路径和它前缀路径组合,而对于两棵子树,这里的两棵子树其中一棵为当前子树,另一棵为即为前面那一堆累计的“子树群”,如上图所示,我们遍历完第一棵的子树的信息不删除,继续累计,就是子树群的信息了。当然常见的也可以先算出总的,然后算补集信息即可。而我们可以开一个桶,记录这些路径长的集合,对于每一种路径长,我们记录它的最小边数,然后拼边即可。
点分治使得可以访问到每个点为根的树的信息维护复杂度降低,其次,我们注意到如果和大于 \(k\) 的前缀路径显然无法拼出等于 \(k\) 的路径长,所以可以剪枝掉,我们用数组当桶即可。
剩余细节见代码注释即可。
参照代码
#include <bits/stdc++.h>
//#pragma GCC optimize("Ofast,unroll-loops")
#define isPbdsFile
#ifdef isPbdsFile
#include <bits/extc++.h>
#else
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
#endif
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
template <typename T>
int disc(T* a, int n)
{
return unique(a + 1, a + n + 1) - (a + 1);
}
template <typename T>
T lowBit(T x)
{
return x & -x;
}
template <typename T>
T Rand(T l, T r)
{
static mt19937 Rand(time(nullptr));
uniform_int_distribution<T> dis(l, r);
return dis(Rand);
}
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
return (a % b + b) % b;
}
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
a %= c;
T1 ans = 1;
for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
return modt(ans, c);
}
template <typename T>
void read(T& x)
{
x = 0;
T sign = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')sign = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
x *= sign;
}
template <typename T, typename... U>
void read(T& x, U&... y)
{
read(x);
read(y...);
}
template <typename T>
void write(T x)
{
if (typeid(x) == typeid(char))return;
if (x < 0)x = -x, putchar('-');
if (x > 9)write(x / 10);
putchar(x % 10 ^ 48);
}
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
write(x), putchar(c);
write(c, y...);
}
template <typename T11, typename T22, typename T33>
struct T3
{
T11 one;
T22 tow;
T33 three;
bool operator<(const T3 other) const
{
if (one == other.one)
{
if (tow == other.tow)return three < other.three;
return tow < other.tow;
}
return one < other.one;
}
T3() { one = tow = three = 0; }
T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
{
}
};
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
if (x < y)x = y;
}
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
if (x > y)x = y;
}
constexpr int N = 1e6 + 10; //k为1e6,桶大小不会超过1e6
constexpr int INF = 1e9 + 7;
int treeMin[N];
pii dist[N]; //包括路径和边数
int cnt; //dist的数量
int maxSon, root, sumSize; //最重儿子,当前根,当前树大小
bool del[N]; //该点是否删除
vector<pii> child[N];
int siz[N];
int k, ans = INF;
int edgeMinSize[N]; //开一个桶,对每个长度的路径记录需要的最小边长
//树重心作为根,算出树重心
inline void makeRoot(const int curr, const int fa)
{
siz[curr] = 1;
int maxSize = 0; //最大子树
for (const auto nxt : child[curr] | views::keys)
{
if (nxt == fa or del[nxt])continue;
makeRoot(nxt, curr);
siz[curr] += siz[nxt];
uMax(maxSize, siz[nxt]);
}
uMax(maxSize, sumSize - siz[curr]); //可能是另一半边子树更大
if (maxSize < maxSon)maxSon = maxSize, root = curr; //更新重心
}
//统计前缀路径和边的数量
inline void get_dis(const int curr, const int fa, const int sum, const int edgeCnt)
{
if (sum > k)return; //剪枝,题目要求和为k,这条边长不要
dist[++cnt] = pii(sum, edgeCnt);
for (const auto [nxt,d] : child[curr])if (nxt != fa and !del[nxt])get_dis(nxt, curr, sum + d, edgeCnt + 1);
}
//统计此子树答案
inline void calc(const int curr)
{
cnt = 0;
edgeMinSize[0] = 0; //可能自身路径就是个符合题意的,加一条长为0,边数为0的路径
for (const auto [nxt,d] : child[curr])
{
if (del[nxt])continue;
int pre = cnt; //方便找到新的子树的dist记录起点
get_dis(nxt, curr, d, 1);
forn(i, pre+1, cnt)uMin(ans, edgeMinSize[k - dist[i].first] + dist[i].second); //两路径凑一边
forn(i, pre+1, cnt)uMin(edgeMinSize[dist[i].first], dist[i].second); //更新对应长度的最小值
}
forn(i, 1, cnt)edgeMinSize[dist[i].first] = INF; //删除这些边
edgeMinSize[0] = INF; //删除该点
}
//点分治
inline void div(const int curr)
{
del[curr] = true;
calc(curr);
for (const auto nxt : child[curr] | views::keys)
{
if (del[nxt])continue;
maxSon = sumSize = siz[nxt];
makeRoot(nxt, 0);
div(root);
}
}
int n;
inline void solve()
{
cin >> n >> k;
forn(i, 1, n-1)
{
int u, v, d;
cin >> u >> v >> d;
++u, ++v; //变为从1开始
child[u].emplace_back(v, d);
child[v].emplace_back(u, d);
}
maxSon = sumSize = n;
fill_n(edgeMinSize, N, INF);
makeRoot(1, 0); //也可以继续考虑重算size减小常数,不过不太需要
div(root);
cout << (ans == INF ? -1 : ans);
}
signed int main()
{
Spider
//------------------------------------------------------
int test = 1;
// read(test);
// cin >> test;
forn(i, 1, test)solve();
// while (cin >> n, n)solve();
// while (cin >> test)solve();
}
\[时间复杂度为 \ O(n\log{n})
\]



