P8078 [WC2022] 秃子酋长题解

题目链接: P8078 [WC2022] 秃子酋长

题目所求较难理解，我们考虑转化下，首先这是个 \(1 \sim n\) 的排列，而且要求相邻对应的原位置的绝对值最大我们先考虑最简单的一种情况：\([1,n]\) 的答案。

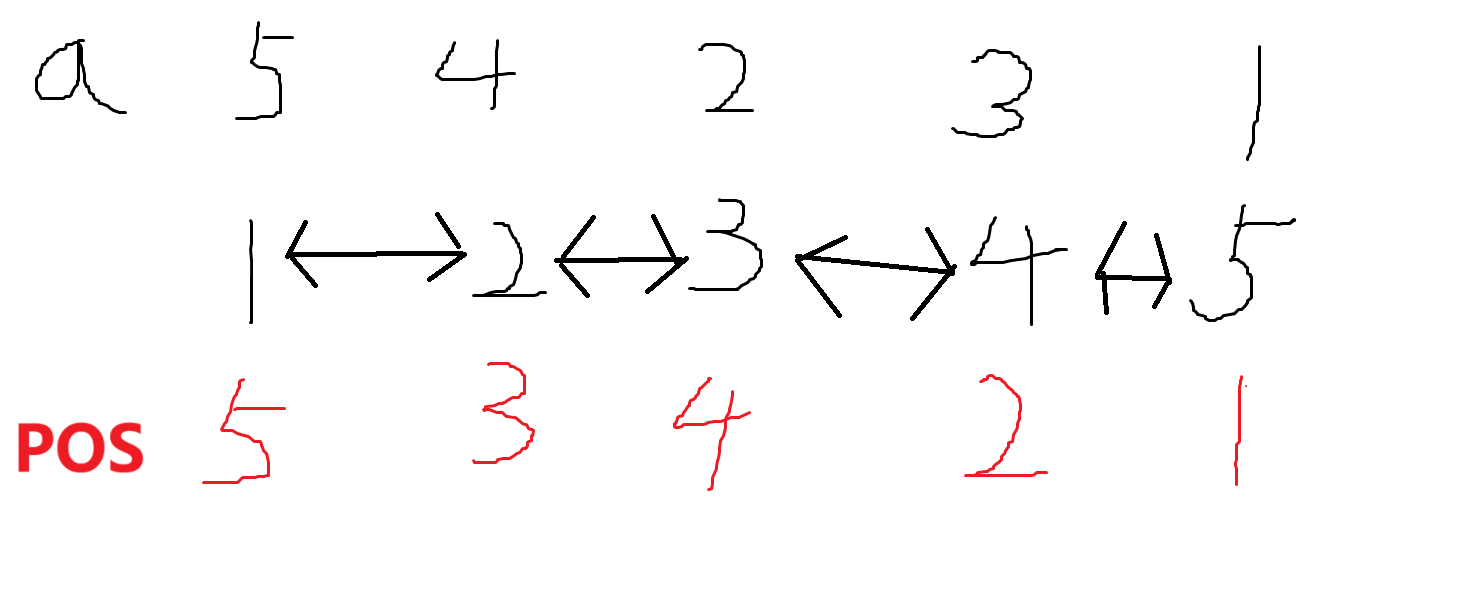
来看这张我画的丑图。以样例为例，如果求 \([1,n]\) 的答案，我们排完序以后，要通过值找到它的原位置的 \(pos\) ，然后相邻的值进行 \(pos\) 绝对值之差之和。

比如这里的答案应该为：

\[ans=\sum_{i=1}^{n-1} \left| pos_{i+1}-pos_i \right|=\left|3-5 \right|+\left| 4-3\right|+\left|2-4 \right|+\left| 1-2 \right|=6 \]

很显然的是，如果第三行这个东西我们建一个双向链表，我们可以很自然的拿到每个位置对应的前后驱，也即是它相邻位置的 \(pos\)。那么考虑对这个链表增加和删除的贡献变化。很自然的是删除很简单，我们删除一个节点 \(pos_i\) 贡献将会有以下变化：

如果它存在前后驱，那么它前后驱会拼起来，得到一个新的 \(\left|pos_{i+1}-pos_{i-1}\right|\) 值。
考虑如果它有前驱，那么会减少一个 \(\left|pos_{i}-pos_{i-1}\right|\)。同理如果有后驱的话，它一样也会减少一个\(\left|pos_{i+1}-pos_{i}\right|\)。
最后我们在把它的前后驱拼在一起，如果存在 \(0\) 也无所谓，因为我们 \(0\) 作为空链表节点，我们本身将它作为 \(NULL\) 不参与贡献，所以直接的，我们有这样一个变化式子：\(pre[nxtPos]=prePos,nxt[prePos]=nxtPos\)。

考虑加法和上述是逆过程。完全反过来。好啦，问题来了，加法这样计算贡献一定对吗？很显然，是有问题的，如果增加的这个节点的相邻的节点已经删除了，我们则会增加一组不存在的贡献，因为我们的判断条件仅仅只是它是否在原来得到有序序列中是否有前后驱。那么分讨？有没有一种“只删不加”的东西？答案是：回滚莫队

回滚莫队与普通莫队的区别

常常的你会听说回滚莫队就两种，只删不加，只加不删。以只删不加为例，回滚莫队真得只有删除没有增加吗？不是的。回归莫队的回滚，更多的是一种回撤的思想。举个例子，如果上述的删某个节点以后再重新把它加回来时，如果这个时间段，其他节点并未发生变化，换句话说，我把删节点的过程倒着做了一遍，这种加法显然就正确了。就好比你把魔方打乱以后，按照你打乱的步骤逆序复原，这个过程一定正确。所以回滚莫队常常会用到许多可撤销的数据结构。

所以回滚莫队在即使同时具有加减法的同时，也能很好地保证每种操作的正确性，因为它需要回滚的加法或者减法在某个时间段是一定互逆正确的。

简单提提回滚莫队的设计。首先呢对于传统莫队而言，我们都是奇偶块优化的，显然不能上了。实际上，这里的只加/只减的核心点是在于 \(r\) 的有序性。不同的块还是按照左端点的块编号排序，相同的块考虑 \(r\) 是顺序还是逆序。逆序的话对于同一个块而言，\(r\) 就是只会减小的，这就是只减不加回滚莫队。反过来就是只加不减的回滚莫队。

在同个块中，\(r\) 只会减小，不用管。我们把 \(l\) 放在块的最左边，那么很显然，它在查询的时候，也是只会减的，当然，回滚莫队的重点也在这，在查询结束以后需要把这个 \(l\) 恢复到原来查询块的左端点处。在这个过程中也有加法，但加法和减法显然是一种“原路返回”的既视感，所以这种加法是完全正确的。
考虑开始处理新的一个块的查询，那么这里的 \(r\) 我们将重新的放置在最右边 \(n\) 处，而 \(l\) 也应该来到新的查询块的最左边。显而易见的是以常见的莫队思想来说，我们通常会拷贝一份在上个块的初识状态数组，用于回撤这个已经做过 \(r\) 删除的数组恢复到原样然后再移动 \(l\)。但对于回滚莫队而言，我们可以直接地重新移动 \(r\) 到 \(n\) 做加法，因为此时此刻 \(l\) 保证不动，还是前一个块的左端点，发生变化的是 \(r\) 的删除，这个过程也可以看做 \(r\) 的回滚。这两种写法都是可以的。这里是最重要的核心回滚思想，需要理解，也是区别普通莫队的最大点。

细节

常见的我们块内暴力，但这题显然在块内暴力需要重新创建链表然后做判断，写起来较为小繁琐，我们可以继续沿用回滚莫队指针移动即可。

\[\text{由于是接近 } O(1) \text{删除的，所以复杂度为 } O(n\sqrt{n}) \]

常规带拷贝份的回滚莫队参照代码

#include <bits/stdc++.h>

//#pragma GCC optimize("Ofast,unroll-loops")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}


template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 5e5 + 10;
int pre[N], nxt[N]; //链表
ll ans;
int pos[N];

struct Mo
{
    int l, r, id;

    bool operator<(const Mo& other) const
    {
        return pos[l] != pos[other.l] ? pos[l] < pos[other.l] : r > other.r;
    }
} node[N];

int n, m;
ll res[N];//答案
int val[N]; //序列原来对应的位置
int last = 1;//上一个查询块编号
int s[N];//块的起点
int precp[N], nxtcp[N]; //用于复制的序列
inline void del(const int curr)
{
    int prePos = pre[curr], nxtPos = nxt[curr];
    if (prePos and nxtPos)ans += abs(nxtPos - prePos); //增加前后相邻的位置绝对值之差
    if (prePos)ans -= abs(curr - prePos); //减少与前面的之差
    if (nxtPos)ans -= abs(curr - nxtPos); //减少与后面之差
    nxt[prePos] = nxtPos;
    pre[nxtPos] = prePos;
}

//可能原本的前驱和后继也被删除了,但回滚莫队需要回滚的回滚以后的前后驱一定保持原样
inline void add(const int pos)
{
    int prePos = pre[pos], nxtPos = nxt[pos];
    if (prePos and nxtPos)ans -= abs(nxtPos - prePos); //减少前后相邻的位置绝对值之差
    if (prePos)ans += abs(pos - prePos); //增加与前面的之差
    if (nxtPos)ans += abs(pos - nxtPos); //增加与后面之差
    pre[nxtPos] = nxt[prePos] = pos;
}

ll preAns;//回滚时需要的答案

inline void solve()
{
    int x;
    read(n, m);
    int siz = sqrt(n);
    int cnt = (n + siz - 1) / siz;
    forn(i, 1, n)read(x), val[x] = i, pos[i] = (i - 1) / siz + 1;
    forn(i, 1, cnt)s[i] = (i - 1) * siz + 1;
    forn(i, 1, n)precp[val[i]] = pre[val[i]] = val[i - 1], nxtcp[val[i]] = nxt[val[i]] = val[i + 1]; //值i对应的前后位置
    forn(i, 1, m)read(node[i].l, node[i].r), node[i].id = i;
    sortArr(node, m);
    forn(i, 1, n-1)ans += abs(val[i + 1] - val[i]); //初始化有[1,n]
    preAns = ans;
    int l = 1, r = n; //位置
    forn(i, 1, m)
    {
        auto [L,R,id] = node[i];
        if (pos[L] != pos[node[i - 1].l])
        {
            //回滚回去,使得当前为[pos[L],n]
            forn(i, 1, n)pre[i] = precp[i], nxt[i] = nxtcp[i];
            ans = preAns;
            while (l < s[pos[L]])del(l++);
            //记录当前块最终回滚需要的状态
            forn(i, 1, n)precp[i] = pre[i], nxtcp[i] = nxt[i];
            preAns = ans;
            r = n;
            last = pos[L];
        }
        while (r > R)del(r--);
        while (l < L)del(l++);
        res[id] = ans;
        //回滚回去
        while (l > s[pos[L]])add(--l);
    }
    forn(i, 1, m)write(endl, res[i]);
}

signed int main()
{
    Spider
    //------------------------------------------------------
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
}

基于回滚思想跨块重置的回滚莫队参照代码

#include <bits/stdc++.h>

//#pragma GCC optimize("Ofast,unroll-loops")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}


template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 5e5 + 10;
int pre[N], nxt[N]; //链表
ll ans;
int pos[N];

struct Mo
{
    int l, r, id;

    bool operator<(const Mo& other) const
    {
        return pos[l] != pos[other.l] ? pos[l] < pos[other.l] : r > other.r;
    }
} node[N];

int n, m;
ll res[N];//答案

inline void del(const int curr)
{
    int prePos = pre[curr], nxtPos = nxt[curr];
    if (prePos and nxtPos)ans += abs(nxtPos - prePos); //增加前后相邻的位置绝对值之差
    if (prePos)ans -= abs(curr - prePos); //减少与前面的之差
    if (nxtPos)ans -= abs(curr - nxtPos); //减少与后面之差
    nxt[prePos] = nxtPos;
    pre[nxtPos] = prePos;
}

//可能原本的前驱和后继也被删除了,但回滚莫队需要回滚的回滚以后的前后驱一定保持原样
inline void add(const int pos)
{
    int prePos = pre[pos], nxtPos = nxt[pos];
    if (prePos and nxtPos)ans -= abs(nxtPos - prePos); //减少前后相邻的位置绝对值之差
    if (prePos)ans += abs(pos - prePos); //增加与前面的之差
    if (nxtPos)ans += abs(pos - nxtPos); //增加与后面之差
    pre[nxtPos] = nxt[prePos] = pos;
}

int val[N]; //序列原来对应的位置
int last;//最后一次查询块编号
int s[N];//块起点
int x;//读入

inline void solve()
{
    read(n, m);
    int siz = sqrt(n);
    int cnt = (n + siz - 1) / siz;
    forn(i, 1, n)read(x), val[x] = i, pos[i] = (i - 1) / siz + 1;
    forn(i, 1, cnt)s[i] = (i - 1) * siz + 1;
    forn(i, 1, n)pre[val[i]] = val[i - 1], nxt[val[i]] = val[i + 1]; //值i对应的前后位置
    forn(i, 1, m)read(node[i].l, node[i].r), node[i].id = i;
    sortArr(node, m);
    forn(i, 1, n-1)ans += abs(val[i + 1] - val[i]); //初始化有[1,n]
    int l = 1, r = n; //位置
    forn(i, 1, m)
    {
        auto [L,R,id] = node[i];
        if (pos[L] != last)
        {
            //回滚回去,使得当前为[pos[L],n],基于回滚思想,add一定正确
            while (r < n)add(++r);
            while (l < s[pos[L]])del(l++);
            last = pos[L];
        }
        while (r > R)del(r--);
        while (l < L)del(l++);
        res[id] = ans;
        //回滚回去
        while (l > s[pos[L]])add(--l);
    }
    forn(i, 1, m)write(endl, res[i]);
}

signed int main()
{
    Spider
    //------------------------------------------------------
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
}

posted @ 2024-01-03 10:24 Athanasy 阅读(62) 评论(0) 编辑收藏举报

刷新页面返回顶部

Athanasy

P8078 [WC2022] 秃子酋长题解

题目链接: P8078 [WC2022] 秃子酋长

题目所求较难理解，我们考虑转化下，首先这是个 \(1 \sim n\) 的排列，而且要求相邻对应的原位置的绝对值最大我们先考虑最简单的一种情况：\([1,n]\) 的答案。

回滚莫队与普通莫队的区别

所以回滚莫队在即使同时具有加减法的同时，也能很好地保证每种操作的正确性，因为它需要回滚的加法或者减法在某个时间段是一定互逆正确的。

细节

公告