网络流
网络流
网络流的概念
在一个有向图上选择一个源点,一个汇点,每一条边上都有一个流量上限(以下称为容量),
即经过这条边的流量不能超过这个上界,同时,除源点和汇点外,所有点的入流和出流都相等,
而源点只有流出的流,汇点只有汇入的流。这样的图叫做网络流。
网络流的相关定义
-
源点:有n个点,有m条有向边,有一个点很特殊,只出不进,叫做源点。
-
汇点:另一个点也很特殊,只进不出,叫做汇点。
-
容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常用c[i,j]表示,流量则通常是f[i,j].
通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最大的车流量。
很显然的,流量<=容量。而对于每个不是源点和汇点的点来说,可以类比的想象成没有存储功能的货物的中转站,
所有“进入”他们的流量和等于所有从他本身“出去”的流量。
- 最大流:把源点比作工厂的话,问题就是求从工厂最大可以发出多少货物,是不至于超过道路的容量限制,也就是,最大流。
Ford-Fulkerson 增广路算法
该方法通过寻找增广路来更新最大流,有 EK,dinic,SAP,ISAP 主流算法。
求解最大流之前,我们先认识一些概念。
最常用的就是dinic(据说隔壁treaker只会这一种)。
但是费用流需要用到EK算法,so,要学会EK算法,dinic;
增广路:在图中若一条从源点到汇点的路径上所有边的 剩余容量都大于 0 (注意是大于不是大于等于),这条路被称为增广路。
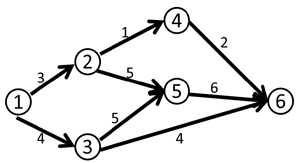
EK算法O(nm2)
求解思路:
从图中找一条增广路,然后增广,怎么找?
1.从源点开始bfs,找到到汇点的一条路径,并记录这条路径上所有边剩余流量最小值,因为要找增广
路,所以我们在bfs时要判断一下边的剩余容量是否为0,记得用一个pre数组记录下路径。
2.找到路径后,对其进行增广(代码里的up函数),增广就是把这条路径的每条边都减去这
些边中剩余流量的最小值(bfs时记录),反向边加上这个最小值(关于方向边下面再解释)。
3.一直找增广路增广,直到不能增广为止(找不到增广路)。
可以看下面这张图。

感谢SYCstudio的图(本人较菜懒不会画)。
上面我们提到了反向边,下面我们解释下为什么要建反向边。(放图,简单图我还是可以的现学的)

像我们上面这张图,因为我们bfs时不能确定第一次走哪条边,要是你像bmf一样运气不好,
如果bfs第一次找到的增广路是1→3→2→1的话,我们最后求得的最大流就是1.
但是很明显这张图最大流是2,所以我们发现第一次找的增广路不是最优的,这时候你就凉了。
那我们怎么解决呢反向边,反向边其实就是一个反悔的机会,也就是让流过的流量流回去。
如果还不明白的话还学什么网络流,下面模拟一下这个过程。
先说一下反向边的一些东西,反向边初始化为0,当正向边剩余流量减少的是时候,
反向边流量增加同样的值,因为我们可以反悔的流量等于已经从这条边正向流过的流量。
下面看一下我们是如何通过反向边反悔的又要做图qaq。
因为我不会画反向边,所以我们假设‘1/0’左边那个数字表示正向变边权,右边是反向边。
下面这张图就是建完边后的图。
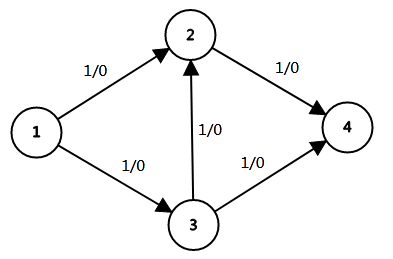
如果我们第一次找到的增广路是1→3→2→1的话,总流量+1=1,图就变成了
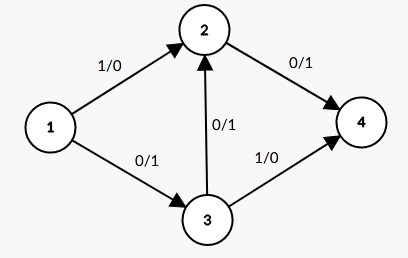
我们发现我们还可以找到增广路1→2→3→4,总流量+1=2,图变成

然后发现,找不到增广路了,程序结束不用作图了,我们发现
再找增广路的过程中3→2这条边正向一次,反向一次,相当于流量为0.
这就是反向边的作用。
另外提供一种小技巧,使用邻接表建图的话,可以边的编号从2开始建,我们知道
2^1=3,3^1=2……
这样的话我们可以通过异或得到反向边的编号(记得建完正向边,紧接着就建反向边),具体看代码
时间复杂度为O(nm2)至于为什么,本人很菜不会,另外,一般时间复杂度是远远达不到这个值的。
代码(EK)
#include<iostream> #include<cstdio> #include<cstring> #include<queue> #define LL long long using namespace std; const int inf=1<<29; const int N=207; const int M=5e3+7; int n,m,s,t,cnt=1;//从编号2开始建边 LL maxf;//最大流 int head[N],vis[N],pre[N]; LL incf[N]; LL v[N][N]; struct edge{ int v,nxt; LL w; }e[M<<1];//因为要建反向边,所以开二倍空间 void add_edge(int u,int v,LL w){//存边 cnt++; e[cnt].v=v; e[cnt].w=w; e[cnt].nxt=head[u]; head[u]=cnt; } bool bfs(){ memset(vis,0,sizeof(vis)); queue<int>q; q.push(s); vis[s]=1; incf[s]=inf; while(q.size()){ int now=q.front();q.pop(); for(int i=head[now];i;i=e[i].nxt){ if(e[i].w==0||vis[e[i].v])continue; int to=e[i].v; incf[to]=min(incf[now],e[i].w);//记录路径最小边的流量 pre[to]=i;//记录路径边的编号 q.push(to); vis[to]=1; if(to==t)return 1; } } return 0; } void up(){ int x=t; while(x!=s){ int i=pre[x]; e[i].w-=incf[t]; e[i^1].w+=incf[t];//反向边加上正向边减少的流量 x=e[i^1].v; } maxf+=incf[t]; } inline int read() { int x = 0 , f = 1; char ch = getchar(); while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();} while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();} return x * f; } int main(){ n = read(); m = read(); s = read(); t = read(); for(int i=1;i<=m;i++){ int x,y,z; x = read(); y = read(); z = read(); v[x][y] += z; } for(int i = 1;i <= n;i ++) for(int j = 1;j <= n;j ++) if(v[i][j]) add_edge(i,j,v[i][j]),add_edge(j,i,0); while(bfs())up(); cout<<maxf<<endl; }//可能跟你们码风不同,╮(╯▽╰)╭
Dinic
会了EK还学dinic有什么用呢,有用,我们来分析下下面这张图不小心把颜色改了下,懒得再做一张。
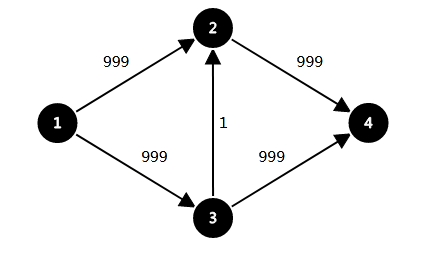
如果你运气不好的话像bmf一样,若你每次找到的增广路都经过了2→3或3→2这条边的话你又凉了
所以这时候就用到了我们的Dinic算法。
Dinic 算法 的过程是这样的:每次增广前,我们先用 BFS 来将图分层。设源点的层数为1 ,
那么一个点的层数便是它离源点的最近距离。
层次用数组dep表示。分层图对于每条边满足dep[v]=dep[u]+1。
我们思考,EK算法每轮可能会遍历整个图,但只找出一条增广路,属于单路增广。
而Dinic属于多路增广,时间复杂度O(n2m)
求解思路:
1.bfs求出节点的层次,构建分层图
2.对于求出的分层图,用dfs进行多路增广,由于本人菜,讲的不是很明白,我们可以看代码
3.当前弧优化 :cur[]数组的应用,如果一条边已经被增广过,那么它就没有可能被增广第二次。那么,我们下一次进行增广的时候,
就可以不必再走那些已经被增广过的边。
#include<bits/stdc++.h> #define LL long long const int N=210; const int M=5e3+7; using namespace std; int n,m,s,t,cnt=1; LL max_flow; int dep[N],head[N],cur[N]; struct edge{ int v,w,nxt; }e[M<<1];//数组含义与上一篇EK含义一样,cur[]数组是dinic的一个优化,下面会提到 void add_edge(int u,int v,int w){ cnt++; e[cnt].v=v; e[cnt].w=w; e[cnt].nxt=head[u]; head[u]=cnt; } int bfs(){//构建分层图 for(int i=1;i<=n;i++) dep[i]=0;//每个节点层次初始化 queue<int>q; q.push(s); dep[s]=1;//源点初始化为1; while(q.size()){ int now=q.front(); q.pop(); for(int i=head[now];i;i=e[i].nxt){ int to=e[i].v,val=e[i].w; if(val&&(!dep[to])){//构建分层图的时候要保证边不为0,如果dep[]已经被更新就不用更新了 q.push(to); dep[to]=dep[now]+1; if(to==t)return 1;//如果到达汇点,进行dfs } } } return 0; } int dfs(int u,int flow){ if(u==t)return flow; int rest=flow,k;//rest表示当前这个节点最大允许通过流量 for(int i=cur[u];i&&rest;i=e[i].nxt){ cur[u]=i;//当前弧优化 int to=e[i].v,val=e[i].w; if(val&&(dep[to]==dep[u]+1)){ int k=dfs(to,min(rest,val));//寻找增广路 if(!k)dep[to]=0;//如果在to之后的路径找不到增广路,踢出分层图 e[i].w-=k;//回溯时更新边权 e[i^1].w+=k; rest-=k;//当前节点最大允许通过流量减去这次通过的流量 } } return flow-rest; } int main(){ scanf("%d%d%d%d",&n,&m,&s,&t); for(int i=1;i<=m;i++){ int x,y,z; scanf("%d%d%d",&x,&y,&z); add_edge(x,y,z); add_edge(y,x,0); } int flow=0; while(bfs()){ for(int i=1;i<=n;i++){ cur[i]=head[i]; //当前弧初始化 } while(flow=dfs(s,1<<29))max_flow+=flow; } cout<<max_flow<<"\n"; }
最小割
最小割问题是指:给出一种有向图(无向图)和两个点s,t以及图中的边的边权,
求一个权值和最小的边集,使得删除这些边之后是s,t不连通。这类问题,一般运用最
大流等于最小流定理,求出最大流来解决。证明自行百度百科
附上代码
int bfs(){ for(int i=1;i<=2*n;i++)dep[i]=0; queue<int>q; q.push(s); dep[s]=1; while(q.size()){ int now=q.front(); q.pop(); for(int i=head[now];i;i=e[i].nxt){ int to=e[i].v,val=e[i].w; if(val&&!dep[to]){ q.push(to); dep[to]=dep[now]+1; if(to==t)return 1; } } } return 0; } int dfs(int u,int flow){ if(u==t)return flow; int rest=flow,k; for(int i=cur[u];i;i=e[i].nxt){ cur[u]=i; int to=e[i].v,val=e[i].w; if(val&&(dep[to]==dep[u]+1)){ k=dfs(to,min(val,rest)); if(!k)dep[to]=0; e[i].w-=k; e[i^1].w+=k; rest-=k; } } return flow-rest; }
费用流
费用流就是每条边除了有容量限制外,还有一个给定的单位费用 w(x,y),
当流过(x,y)这条边时,要花费 f(x,y)*w(x,y)的费用
一般求解的问题是最小费用最大流和最大费用最大流,
基于之前提到的Ek算法,把bfs改成spfa即可,
就是每次先增广费用最小的流。。。
int spfa(){//最小费用最大流 for(int i=0;i<=n;i++)dis[i]=inf,vis[i]=0; queue<int>q; q.push(s); dis[s]=0; vis[s]=1; incf[s]=inf; while(q.size()){ int now=q.front(); vis[now]=0; q.pop(); for(int i=head[now];i;i=e[i].nxt){ int to=e[i].v,val=e[i].w; if(!val)continue; if(dis[to]>dis[now]+e[i].f){ dis[to]=dis[now]+e[i].f; incf[to]=min(incf[now],val); pre[to]=i; if(!vis[to]){ vis[to]=1; q.push(to); } } } } if(dis[t]==inf)return 0; return 1; } int up(){ int x=t; max_flow+=incf[t]; min_cost+=dis[t]*incf[t]; while(x!=s){ int i=pre[x]; e[i].w-=incf[t]; e[i^1].w+=incf[t]; x=e[i^1].v; } }
end......



 浙公网安备 33010602011771号
浙公网安备 33010602011771号