树和二叉树
树
不同于队列、栈等一对一的数据结构,树是一对多的数据结构。树(Tree)是n(n>=0)各节点的有限集。当n=0,为空树。
在任意一颗非空树中:
- 有且只有一个特定的结点称为:根(Root)
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、...Tm。其中每一个树本身又是一棵树,并且称为:子树。
两点注意:
- n>0时候,根节点唯一。
- m>0时候,子树个数虽然没有限制。但是他们不会相交(不会形成类似环状的形状)
树的结点
结点:
度:结点拥有的子树个数称之为结点的度。整棵树的度:各结点度的值的最大值。
- 度为0的结点称为:叶节点或者终端结点
- 度不为0的结点称为:分支结点
- 度不为0且不是根节点的结点称为:内部结点。
(附截图)

结点关系
- Child:结点子树的根;Parent:相应的,该结点就是Parent
- Sibling(兄弟):统一Parent的Child之间的关系
- 祖先结点:从根到该结点所经过的分支上的所有结点。
深度或高度:
树中结点的最大层次称为输的深度或高度。下面截图就是高度和度均为3的一棵树:

其它定义
有序树和无序树:
如果将树中结点的各子树看成从左到右有次序的,不能互换的,就是有序树;否则就是无序树。
森林:
是m>0棵互不相交的树的结合。对树中每个结点,其子树的集合就是森立。
二叉树
特点:
- 二叉树的度<=2。
- 二叉树是有序树。
五种基本形态
截图
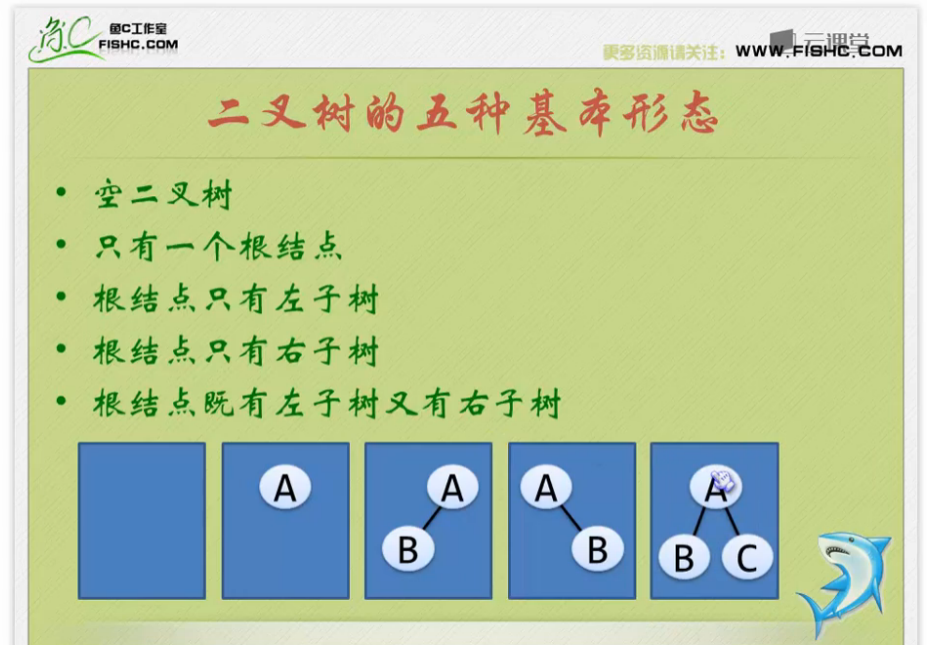
特殊二叉树
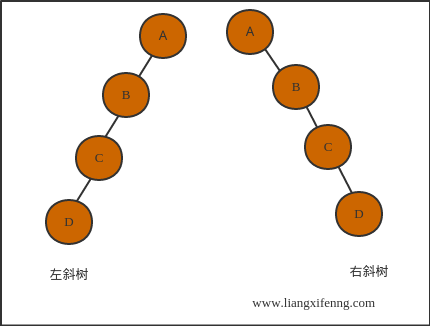
- 斜二叉树
- 左斜树:所有结点都只有左子树的二叉树;
- 右斜树:所有结点都只有右子树的二叉树;截图
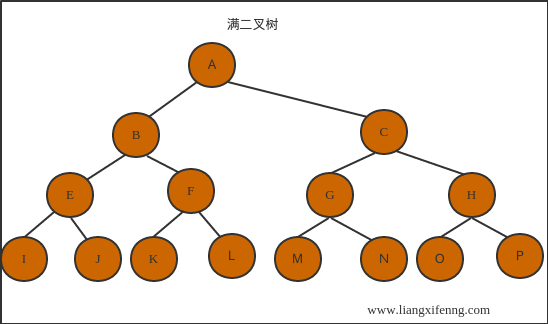
- 满二叉树
- 所有分支结点的度为2;
- 所有叶子结点只能分布在最下层上;
- 同样深度的二叉树中,满二叉树的结点数最多,叶子结点数最多;
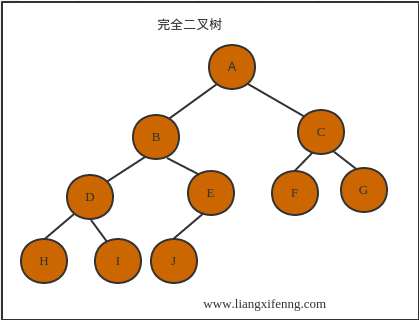
- 完全二叉树
- 所有叶子结点只能出现在最下两层
- 若结点度为1,则该结点只有左子树,不存在只有右子树的情况
- 结点分配 先左后右
通过截图1和截图2看一下满二叉树和完全二叉树的区别:
欢迎进一步交流本博文相关内容:
博客园地址 : http://www.cnblogs.com/AsuraDong/
CSDN地址 : http://blog.csdn.net/asuradong
也可以致信进行交流 : xiaochiyijiu@163.com
欢迎转载 , 但请指明出处 : )
数学性质
-
二叉树的第i层上最多有2^(i-1)个结点(i>=1)
-
深度为k的二叉树最多有2^k-1 个结点
-
如果中断节点数为n0,度为2的节点数为n2,那么n0 = n2+1 ...(1)
推导:
设度为1的节点数为n1。那么 总结点数 n= n0+n1+n2连接数(连接线)为n-1。通过图易得 也等于 n1+2*n2。
所以n-1 = n1+2*n2.......(2)
联立等式(1).(2)可得到性质三。
-
具有n个结点的完全二叉树的深度为[log_2 n]+1
推导:
深度为k的满二叉树结点为n = 2^k-1 。所以k = log_2(n+1)。而完全二叉树叶子结点在最下面两层。所以,倒数第二层以上的满二叉树 n = 2^(k-1)-1 。
So : 2^(k-1)<= n <= 2^k-1
So: 2^(k-1)<= n < 2^k
So: k-1<= log_2 n <k
所以:k = [log_2 n ]+1
-
(见截图)。效果见截图。注意结点的排序,从上到下,从左到右。

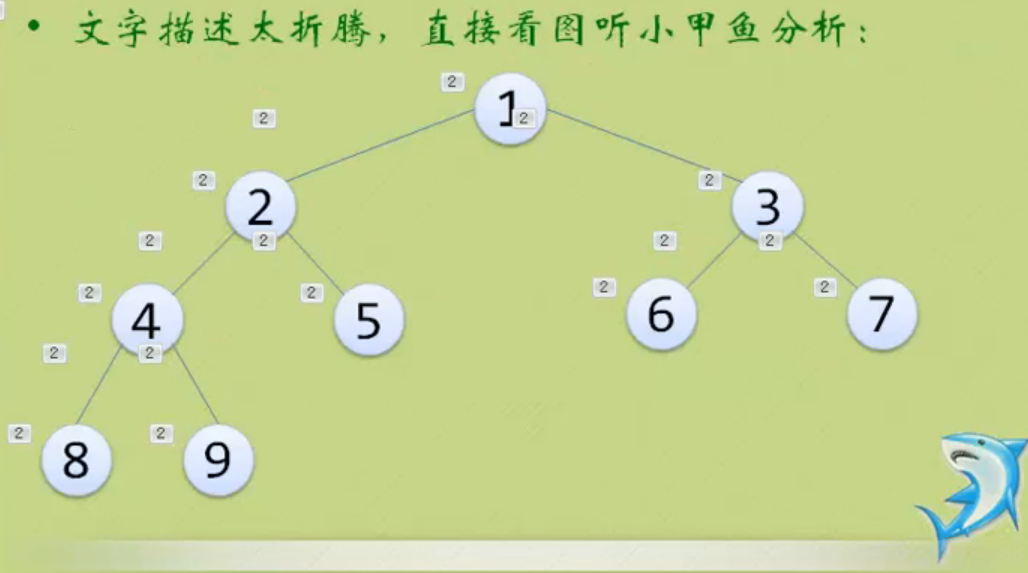
二叉树建立和遍历代码实现
二叉树的存储结构
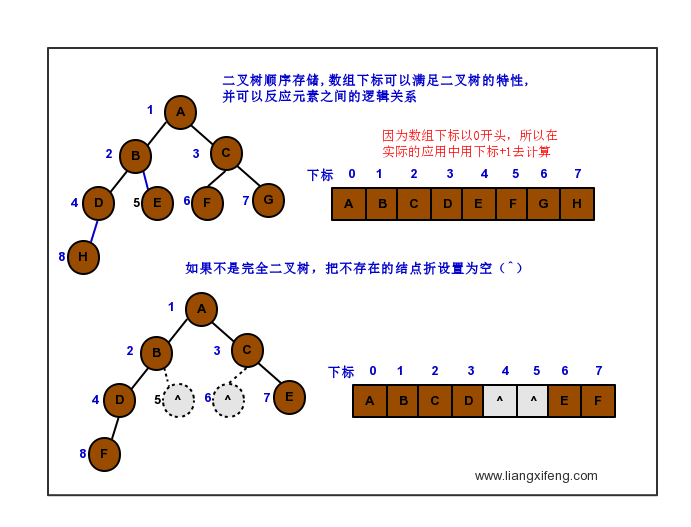
- 顺序存储,方便查询操作,并且可以根据层序遍历,合理的利用以上特性(截图)
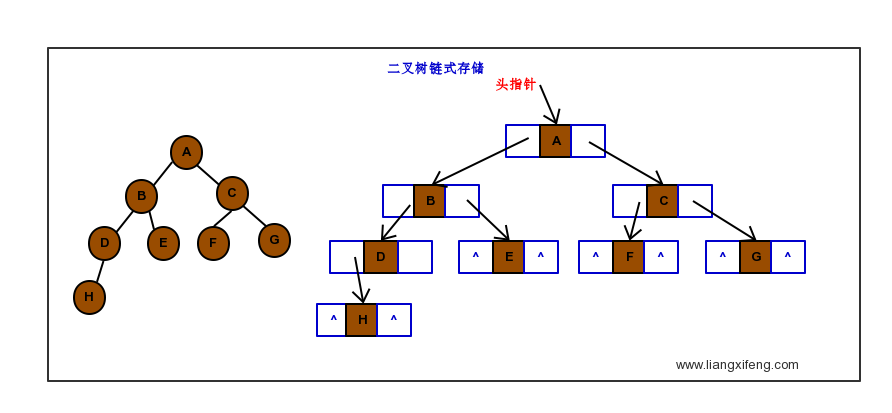
- 链式存储,方便新增,删除操作;结构为数据域+左孩子指针+右孩子指针 (二叉链表),如果有必要的情况下可以添加双亲指针,指向结点的双亲(三叉链表),这都是根据业务需求 灵活控制 的。(截图)
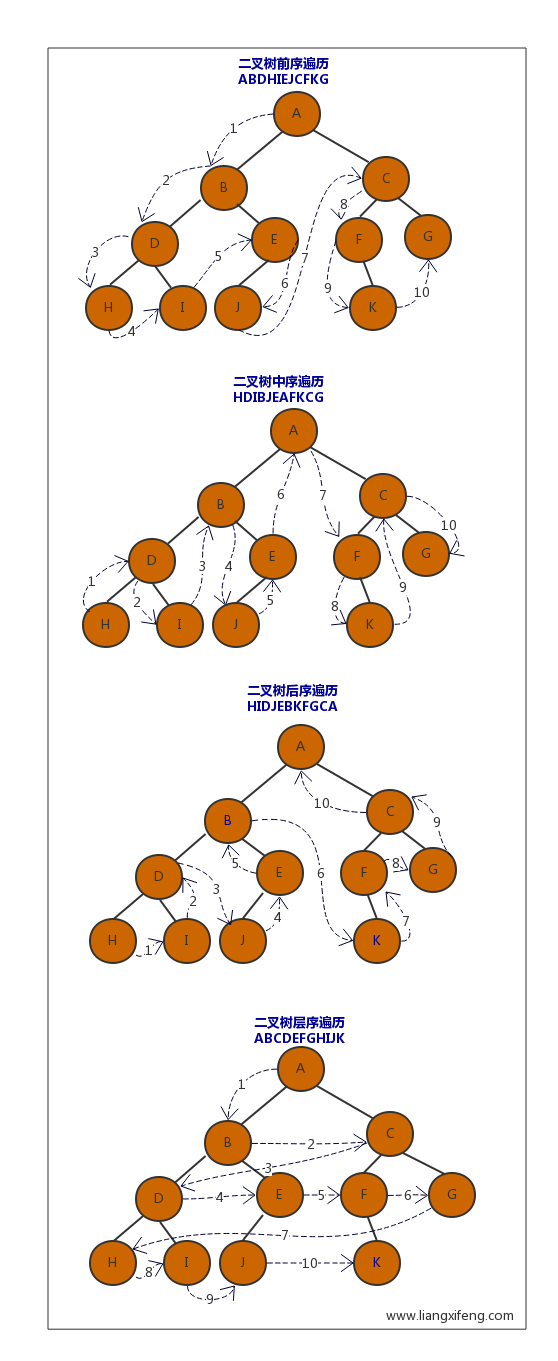
二叉树的遍历方式
有三种遍历方式。命名的根据是按照根节点被遍历的顺序。前序、中序 || 后序、中序 可以确定一个二叉树。但是前序+后序不可以确定一颗二叉树。
- 前序:先访问根结点 -> 遍历左子树 -> 遍历右子树;先访问根结点
- 中序:遍历左子树 -> 访问根结点 -> 遍历右子树;中间访问根结点
- 后序:遍历左子树 -> 遍历右子树 -> 后访问根结点;后访问根结点
- 层序:自上而下,从左到右逐层访问结点;
下面截图展现了4中遍历方式。
代码实现
#include<iostream>
#include<cstdio>
using namespace std;
typedef char ElemType;
struct BinTree{
ElemType data;
BinTree *lchild,*rchild;//左子树和右子树
};
//按照前序遍历创建二叉树。注意输入的顺序也必须得是前序遍历的顺序。
void CreateBinTree(BinTree *&T){
ElemType c;
scanf("%c",&c);
if(c!=' '){
T = new BinTree;
T->data = c;
CreateBinTree(T->lchild);//递归创建
CreateBinTree(T->rchild);
}
else
T = NULL;//空格代表是空子树
}
//递归查找二叉树的深度
int BinTreeDepth(BinTree *T){
int left_depth,right_depth;
if(T==NULL) return 0;
else{
left_depth = BinTreeDepth(T->lchild)+1;
right_depth = BinTreeDepth(T->rchild)+1;
return left_depth>=right_depth?left_depth:right_depth; //返回最大深度
}
}
//按照前序遍历二叉树
//中序和后序只需要改变if(T)条件中语句顺序
void PreOrderBinTree(BinTree *T,int level){
if(T){
cout<<"在第"<<level<<"层,"<<"数据是:"<<T->data<<endl;
PreOrderBinTree(T->lchild,level+1);//遍历左子树
PreOrderBinTree(T->rchild,level+1);//遍历右子树
}
}
//清空二叉树。注意if中自调用和delete语句的顺序
void ClearBinTree(BinTree *&T){
if(T){
ClearBinTree(T->lchild);
ClearBinTree(T->rchild);
delete T;
}
}
//查找含有对应数据的结点。返回值是结点的指针
BinTree* FindNode(BinTree *T ,ElemType data){
if(T==NULL)
return NULL;
else
if(T->data == data)
return T;
else{
BinTree *tem=NULL;
if(tem=FindNode(T->lchild,data))
return tem;
else if(tem=FindNode(T->rchild,data))
return tem;
else
return tem;
}
}
//输入为(注意空格):AB D CE
int main(){
int level = 1;
BinTree *T = NULL;
CreateBinTree(T) ;
PreOrderBinTree(T,level);
cout<<"二叉树的深度是:"<<BinTreeDepth(T)<<endl;
BinTree *NodeD = FindNode(T,'D');
cout<<NodeD->data<<endl;
return 0;
}



