【牛客网多校第一场】A

题目链接：https://www.nowcoder.com/acm/contest/139/A

 

题意：大概就是给你0，1，2让你填矩阵问有多少种填法满足

a(i,j)<=a(i+1,j)以及a(i,j)<=a(i,j+1)

 

题解：Lindström–Gessel–Viennot lemm这个定理的应用。

本鶸也是第一次看见这种东西。去稍微了解了一下。是一个求不相交路径的东西。

给定n个起点，n个终点，不相交路径的方法数的矩阵行列式如下。

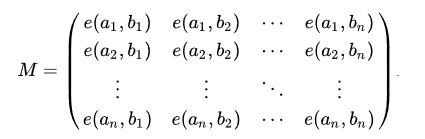
其中e(a,b)为图上a到b的方案数。

 

题解上的ppt给的思路是，

其实也就是把所有的0往左上角搬，2往所有的右下角搬。（感谢bang哥的指导）

 

打个组合的板子，用公式一带就行了！。

 

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long
const ll mod=1e9+7;
const int maxn=2010;
ll c[maxn][maxn];

int main(){
    ll n,m;
//递推求组合数 
    c[1][1] = 1;
    c[0][0] = c[1][0] = 1;
    for(int i = 2 ; i < maxn ; i++){
        c[i][0] = 0;
        for(int j = 0 ; j <= i; j++) 
            c[i][j] = ( c[i-1][j] + c[i-1][j-1] ) % mod;
    }
  
    while(scanf("%lld%lld",&n,&m)==2){
        printf("%lld\n",(c[n+m][n]*c[m+n][n]%mod-c[n+m][m-1]*c[n+m][n-1]%mod+mod)%mod);
    }
    return 0;
}