【美团点评】2020校招数据分析方向笔试题

这几天做了下美团校招的一些套题。（只写了编程，这两天慢慢更新吧）

 

这套题还是蛮简单的。。我暴力了好几个都能过。一个小时多一点差不多能写完。

---

 

试题链接：美团点评2020校招数据分析方向笔试题

 

4、棋子翻转

题意：在4*4的棋盘上摆满了黑白棋子，黑白两色的位置和数目随机其中左上角坐标为(1,1),右下角坐标为(4,4),现在依次有一些翻转操作，要对一些给定支点坐标为中心的上下左右四个棋子的颜色进行翻转，请计算出翻转后的棋盘颜色。

 

题解：这题有点坑，输入输出数据类型都是字符串，我可能leetcode刷多了以为是vector然后一直报段错误。

我用了极其暴力的手法做了输入的处理。。因为这个字符串是固定了长度的。。所以。。看代码吧。

 

代码：

 

#include<bits/stdc++.h>
using namespace std;
int mp[5][5];
int pos[4][4];
string s;
string p;

void init(){
    cin>>s;
    cin>>p;
    mp[0][0] = s[2]-'0';
    mp[0][1] = s[4]-'0';
    mp[0][2] = s[6]-'0';
    mp[0][3] = s[8]-'0';

    mp[1][0] = s[12]-'0';
    mp[1][1] = s[14]-'0';
    mp[1][2] = s[16]-'0';
    mp[1][3] = s[18]-'0';

    mp[2][0] = s[22]-'0';
    mp[2][1] = s[24]-'0';
    mp[2][2] = s[26]-'0';
    mp[2][3] = s[28]-'0';

    mp[3][0] = s[32]-'0';
    mp[3][1] = s[34]-'0';
    mp[3][2] = s[36]-'0';
    mp[3][3] = s[38]-'0';

    pos[0][0] = p[2]-'0';
    pos[0][1] = p[4]-'0';

    pos[1][0] = p[8]-'0';
    pos[1][1] = p[10]-'0';

    pos[2][0] = p[14]-'0';
    pos[2][1] = p[16]-'0';

}

int main(){
    init();
    int x,y;
    for(int i = 0; i < 3; i++){
        x = pos[i][0];
        y = pos[i][1];
        x--;y--;
        if(x-1 >= 0)
            mp[x-1][y] = !mp[x-1][y];
        if(x+1 < 4)
            mp[x+1][y] = !mp[x+1][y];
        if(y-1 >= 0)
            mp[x][y-1] = !mp[x][y-1];
        if(y+1 < 4)
            mp[x][y+1] = !mp[x][y+1];
    }
    cout<<"[";
    for(int i = 0 ;i < 4;i++){
        cout<<"[";
        for(int j = 0; j < 3 ;j++){
            cout<<mp[i][j]<<",";
        }
        if(i == 3)  cout<<mp[i][3]<<"]";
        else    cout<<mp[i][3]<<"],";
    }
    cout<<"]"<<endl;
    
    return 0;
}

 

 

 

5、寻找最后的山峰

题意：山峰元素是指其值大于或等于左右相邻值的元素。给定一个输入数组nums，任意两个相邻元素值不相等，数组可能包含多个山峰。找到索引最大的那个山峰元素并返回其索引。假设 nums[-1] = nums[n] = -∞。

 

题解：感觉也是一个模拟。。一次循环，判断一下左右，满不满足条件。因为是找索引最大。。遍历完就行了。

最后找一个特判，就是最后一个数是不是大于左边的数就可以了。

优化当然也是可以，用二分可行。

 

代码：

#include<bits/stdc++.h>
using namespace std;
 
vector<int> num;
int main(){
    int n;
    while(cin>>n){
        num.push_back(n);
    }
     
    int len = num.size();
    int pos = 0;
    for(int i = 1 ;i < len-1; i++){
        if(num[i]>=num[i+1] && num[i]>=num[i-1]){
            pos = i;
        }
    }
       
    if(num[len-1] > num[len-2])    pos = len-1;
    cout<<pos<<endl;
     
    return 0;
}

 

 

6、比大小

题意：给定一个整数数组，返回一个数组。该返回数组中第i个数字为，原数组中第i个位置的数字至少往右走多少步才能遇到比它大的数字。如果遇不到或者已经处于最右的位置，则置为-1。

 

题解：这个题暴力是会超时的。做优化。参考了一下讨论区大佬的代码，用单调栈做处理。

这样每次比较栈顶元素和当前元素，我们保存栈顶元素的这个步数就好了，也就是找栈顶的大元素。

友情提示：切c++14编译器。

 

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;

int num[maxn];
int ans[maxn]={0};
int main(){
    int n;
    cin>>n;
    for(int i = 0; i < n ;i++){
        cin>>num[i];
        ans[i] = -1;
    }
    stack<int> s;
    
    int cnt = 0;
    while(cnt < n){
        if(!s.empty() && num[s.top()] < num[cnt]){
            int xx = s.top();
            s.pop();
            ans[xx] = cnt - xx;
        }
        else{
            s.push(cnt);
            cnt++;
        }
    }

    for(int i = 0; i < n ;i++){
        cout<<ans[i]<<endl;
    }
    
    return 0;
}

 

 

7、关联查询

题意：数据对象data1List，员工表，存储员工ID，员工姓名

数据对象data2List， 员工工作时长表，存储员工ID，月份，工时

计算每个员工1-3月每月工时及总工时

 

题解：我好像做复杂了。。就是一个模拟题。。我甚至怀疑只有一组数据。。理解题意就行了。

 

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1010;

map<string,int> mp;

struct member{
    int id;
    string name;
    int sumtime;
};

member peo[maxn];

int main(){
    int cnt = 0;
    while(cin>>peo[cnt].id>>peo[cnt].name){
        int id;
        string month;
        int time;
        cin>>id;
        for(int i = 0; i < 3; i++){
            cin>>month>>time;
            mp[month] = time;
        }
        peo[cnt].sumtime = mp["01"]+mp["02"]+mp["03"];
        cout<<peo[cnt].name<<" "<<mp["01"]<<" "<<mp["02"]<<" "<<mp["03"]<<" "<<peo[cnt].sumtime<<endl;
        cnt++;
    }
 
    
    return 0;
}

 

 

8、滑动窗口的中位数

题意：在实时计算中，数据流源源不断地流入计算单元，经常需要借助窗口来处理数据，其中有一类窗口为滑动窗口（Sliding Window），其特点是窗口长度固定，每次滑动一定的位移（slide）

 

 

 

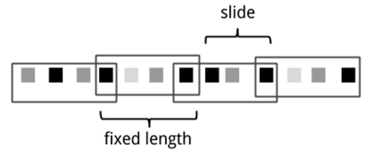
现给定一个数组 nums，有一个长度为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。注意你只可以看到在滑动窗口 k 内的数字，滑动位移大小slide=1，即滑动窗口每次只向右移动一位。

要求返回每一个滑动窗口内的中位数，解释中位数定义，例如：对于[2,3,4]，中位数是3；对于[2,3]，中位数是 (2 + 3) / 2 = 2.5

注意：为了简化窗口计算，规定如果没有累计到窗口大小的数，不能触发计算，即不输出结果！

 

题解：暴力可过。每次对窗口里的元素排序，得到中位数即可。

 

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1010;
 
double num[maxn];
vector<double> res;
int main(){
    int n,k;
    cin>>n>>k;
    for(int i = 0; i < n; i++){
        cin>>num[i];
    }
    int flag = 0;
    if(k%2)    flag = 1;
     
    for(int i = 0; i <= n-k; i++){
        for( int j = i; j < i+k ;j++){
            res.push_back(num[j]);
        }
        sort(res.begin(),res.end());
         
        if(flag)    num[i] = res[k/2];
        else    num[i] = (res[k/2 - 1] + res[k/2]) / 2;
         
        res.clear();
    }
     
    for(int i = 0; i <= n-k; i++){
        printf("%.1lf ",num[i]);
    }
     
    return 0;
}

 

 

9、月份天数

题意：输入年份月份，请输出这个月的天数

 

题解：也是个做了很多遍的题。判断闰年。

闰年：1、能被4整除但是不能被100整除。2、能被400整除。

满足以上条件随便一个就行。

 

代码：

#include<bits/stdc++.h>
using namespace std;
 
bool judge(int year){
    if(year%4 == 0 && year%100)    return true;
    if(year%400 == 0)    return true;
     
    return false;
}
 
int main(){
    int year,month;
    while(cin>>year>>month){
        int flag = 0;
        if(judge(year))    flag = 1;
        if(month == 1 || month == 3 || month == 5 || month == 7||
           month == 8 || month == 10 || month == 12){
            cout<<31<<endl;
        }
        else if(month == 2){
            if(flag)    cout<<29<<endl;
            else    cout<<28<<endl;
        }
        else cout<<30<<endl;
    }
    return 0;
}

 

 

10、整数分解

题意：一个正整数N可以分解为M(M>1)个正整数的和，即N=K+L，例如N=5、M=2时可以分解为(1+4,2+3)。

给定一个正整数N(1<N<200)及正整数M(1<M<200)，求有多少种可能的分解组合(注：K+L和L+K算一种)

 

题解：整数分解也是比较经典的题目。一般我会先用dfs，再用dp。

= =牛客这个编译器有毒，dfs得用c写才行。要不然报段错误。dfs超时,dp应该是正解。

但是都不给AC。我看讨论区也没人过，应该题目有点问题。。

我会给出两份代码。

1、dfs。普通爆搜一定会超时，所以这里说的dfs是做了剪枝处理的。枚举的时候从上一次的划分枚举到sum+i*(m-cur)<=n，因为后面再继续划分一定会大于当前所用分数。所以直接剪枝而不是枚举到n。

2、dp。dp[i][j]表示i可以分成j份的方案。i中分j份可以为：i-1中分j-1份，和i-j中分j份。

初始化只需要做一个dp[0][0]=1。

 

代码：

//深搜
#include<bits/stdc++.h>
using namespace std;
int n,m;
int cnt = 0;


void dfs(int res,int sum,int cur){
    if(cur == m){
        if(sum == n) cnt++;
        return;
    }
    for(int i = res; sum+i*(m-cur)<=n ; i++){
        dfs(i,sum+i,cur+1);
    }

}
int main(){
    cin>>n>>m;
    dfs(1,0,0);
    cout<<cnt<<endl;


    return 0;
}



//dp
#include<bits/stdc++.h>
using namespace std;
const int maxn = 210;
int n,m;
int dp[maxn][maxn]={0};

int main(){
    cin>>n>>m;
    dp[0][0] = 1;

    for(int i = 1; i <= n ;i++){
        for(int j = 1; j <= m ;j++){
            dp[i][j] += dp[i-1][j-1];
            if(i>=j) dp[i][j]+=dp[i-j][j];
        }
    }

    cout<<dp[n][m]<<endl;

    return 0;
}