【数据结构】严蔚敏笔记整理

时隔多日的复更。

本鶸备考过程中整理了一下部分的数据结构的笔记以及严奶奶书上的代码。

不算全面，笔记有错的地方还请指出嗷QWQ。

---

 

 

 

#include<bits/stdc++.h>
using namespace std;


/*基本操作
InitList(&L);       //构造一个空的线性表
DeStroyList(&L);    //销毁一个线性表
ClearList(&L);      //置空表
ListEmpty(L);       //判断空表
ListLength(L);      //返回L中数据元素的个数
GetELem(L,i,&e);    //返回L中第i个数据元素的值
LocateElem(L,e,compare());  //和e满足位序
PriorElem(L,cur_e,&pre_e);  //返回前驱
NextElem(L,cur_e,&pre_e);   //返回后继
ListInsert(&L,i,e);         //在第i个前插入元素e
ListDelete(&L,i,&e);        //删除L的第i个数据元素
ListTraverse(L,visit());    //没个数据元素访问一次

*/

//线性表
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
typedef struct{
    ELemType *elem;     //基址
    int length;         //长度
    int listsize;       //分配的存储容量
}SqList;

Status InitList(SqList &L){
    L.elem = (ELemType *)malloc(LIST_INIT_SIZE*sizeof(ELemType));
    if(!L.elem) return ERROR;
    L.length = 0;                   //空表长度为0
    L.listsize = LIST_INIT_SIZE;    //初始存储容量
    return OK;
}

Status ListInsert(SqList &L,int i,ELemType e){
    if(i < 1 || i > L.length + 1)   return ERROR;
    if(L.length >= L.listsize){
        newbase = (ELemType *)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ELemType));
        if(!newbase)    return ERROR;
        L.elem = newbase;
        L.listsize += LISTINCREMENT;
    }
    q = &(L.elem[L.length-1]; p >= q; --p)  *(p+1) = *p;
    *q = e;
    ++L.length;
    return OK;
}

Status ListDelete(SqList &L,int i,ELemType &e){
    if((i<1)||(i>L.length)) return ERROR;
    p = &(L.elem[i-1]);
    e = *p;
    q = L.elem + L.length-1;
    for(++p; p<= q; ++p)    *(p-1) = *p;
    --L.length;
    return OK;
}


void MergeList(SqList La,SqList Lb,SqList &Lc){
    pa = La.elem; pb = Lb.elem;
    Lc.listsize = Lc.length = La.length + Lb.length;
    pc = Lc.elem = (ELemType *)malloc(Lc.listsize * sizeof(ELemType));
    if(!Lc.elem)    return ERROR;
    pa_last = La.elem + La.length-1;
    pb_last = Lb.elem + Lb.length-1;
    while(pa <= pa_last && pb <= pb_last){
        if(*pa <= *pb)  *pc++ = *pa++;
        else    *pc++ = *pb++;
    }
    while(pa <= pa_last)    *pc++ = *pa++;
    while(pb <= pb_last)    *pc++ = *pb++;
}

//链表
typedef struct LNode{
    ELemType data;
    struct LNode *next;
}LNode, *LinkList;

Status ListInsert(LinkList &L,int i,ELemType e){
    p = L; j = 0;
    while(p && j < i-1 ){       //寻找第i-1个结点
        p = p->next;
        ++j;
    }           
    if(!p || j > i-1)   return ERROR;
    s = (LinkList)malloc(sizeof(LNode));
    s->data = e; s->next = p->next;
    p->next = s;
    return OK;
}

Status ListDelete(LinkList &L,int i,ELemType &e){
    p = L; j = 0;
    while(p->next && j < i-1){
        p = p->next; ++j;
    }
    if(!(p->next) || j > i-1)   return ERROR;
    q = p->next; p->next = q->next;
    e = q->data;    free(q);
    return OK;
}

void MergeList(LinkList &La,LinkList &Lb,LinkList &Lc){
    pa = La->next;  pb = Lb->next;
    Lc = pc = La;
    while(pa && pb){
        if(pa->data <= pb->data){
            pc->next = pa;  pc = pa;    pa = pa->next;
        }
        else{
            pc->next = pb;  pc = pb;    pb = pb->next;
        }
    }
    pc->next = pa ? pa : pb;
    free(Lb);
}



//双向链表
typedef struct DuLNode{
    ELemType data;
    struct DuLNode *prior;
    struct DuLNode *next;
}DuLNode,*DuLinkList;

Status ListInsert(DuLinkList &L,int i,ELemType e){
    if(!(p = GetELem(L,i))) return ERROR;
    if(!(s = (DuLinkList)malloc(sizeof(DuLNode))))  return ERROR;
    s->data = e;
    s->prior = p->prior;    p->prior->next = s;
    s->next = p;    p->prior = s;
    return OK;
}
Status ListDelete(DuLinkList &L,int i,ELemType &e){
    if(!(p = GetELem(L,i))) return ERROR;
    e = p->data;
    p->prior->next = p->next;
    p->next->prior = p->prior;
    free(p);    return OK;
}




int main(){

    return 0;
}

 

---

 

 

 

#include<bits/stdc++.h>

using namespace std;


#define MaxSize 50
typedef struct {
    ElemType data[MaxSize];     //存放栈中元素
    int top;    //栈顶
}SqStack;

//进栈
bool Push(SqStack &S,ElemType x){
    if(S.top == MaxSize-1)  return FALSE:
    S.data[++S.top] = x;        //指针先加1，再入栈
    return TRUE; 
}

//出栈
bool Pop(SqStack &S,ElemType &x){
    if(S.top == -1) return FALSE;
    x = S.data[S.top--];        //先出栈，指针再减1
    return true;
}

//栈顶
bool GetTop(SqStack S,ElemType &x){
    if(S.top == -1) return FALSE;
    x = S.data[S.top];
    return TRUE;
}

//初始化如果是S.top = 0; 
//入栈 S.data[S.top++]; 出栈 S.data[--S.top];

typedef struct Linknode{
    ElemType data;          //数据域
    struct  Linknode *next; //指针域
}*LiStack;                  //栈类型顶定义



//队列
typedef struct{
    ElemType data[MaxSize];     //存放队列元素
    int front,rear;             //队头和队尾指针
}SqQueue;

//循环队列
//入队
bool EnQueue(SqQueue &Q，ElemType x){
    if((Q.rear+1) % MaxSize == Q.front) return FALSE;
    Q.data[Q.rear] = x;
    Q,rear = (Q.rear + 1) % MaxSize;
    return TRUE;
}

bool DeQueue(SqQueue &Q,ElemType &x){
    if(Q.rear == Q.front)   return false;
    x = Q.data[Q.front];
    Q.front == (Q.front + 1) % MaxSize
    return true;
}



int main(){


    return 0;
}

 

---

 

 

 

 

 

 

#include<bits/stdc++.h>
using namespace std;

/*
基本操作
InitBiTree(&T);                 //构造空二叉树
DestoryBiTree(&T);              //销毁二叉树
CreateBiTree(&T,definition);    //按照definition构造二叉树
ClearBiTree(&T);                //清空二叉树
BiTreeEmpty(T);                 //判断是否为空二叉树，空为True  
BiTreeDepth(T);                 //返回T的深度
Root(T);                        //返回T的根
Value(T,e);                     //e为结点，返回e的值
Assign(T,&e,value);             //结点e赋值为value
Parent(T,e);                    //返回e的双亲节点
LeftChild(T,e);                 //返回e的左孩子
RightChile(T,e);                //返回e的右孩子
LeftSibling(T,e);               //返回e的左兄弟
RightSibling(T,e);              //返回e的右兄弟
InsertChild(T,p,LR,c);          //p指向T中结点，LR=0/1，插入c为T中p所指结点的左或右子树
DeleteChild(T,p,LR);            //p指向T中结点，LR=0/1,删除T中p所指结点的左或右子树
PreOrderTraverse(T,Visit());    //先序遍历
InOrderTraverse(T,Visit());     //中序遍历
PostOrderTraverse(T,Visit());   //后序遍历
LevelOrderTraverse(T,Visit());  //层序遍历
*/


//二叉链表存储
typedef struct BiTNode{
    TElemType data;
    struct BiTNode *lchild,*rchild;    
}BiTNode,*BiTree;

//基本操作
Status CreateBiTree(BiTree &T);
Status PreOrderTraverse(BiTree T,Status(* Visit)(TElemType e));
Status InOrderTraverse(BiTree T,Status(* Visit)(TElemType e));
Status PostOrderTraverse(BiTree T,Status(* Visit)(TElemType e));
Status LevelOrderTraverse(BiTree T,Status(* Visit)(TElemType e));

//Visit函数
Status PrintElement(TElemType e){
    printf(e);
    return OK;
}

/***********课本**************/
//二叉链表的先序遍历
//递归
Status PreOrderTraverse(BiTree T, Status(* Visit)(TElemType e)){
    if(T){
        if(Visit(T->data)){
            if(PreOrderTraverse(T->lchild,Visit)){
                if(PreOrderTraverse(T->rchild)) return OK;
            }
        }
        return ERROR;
    }
    else    return OK;
}


//二叉链表的中序遍历
//借助栈，非递归
Status InOrderTraverse(BiTree T,Status(* Visit)(TElemType)){
    InitStack(S);   Push(S,T);  //根指针入栈
    while(!StackEmpty(S)){
        while(GetTop(S,p) && p) Push(S,p->lchild);  //向左走到尽头
        Pop(S,p);       //空指针退栈
        if(!StackEmpty(S)){         //访问结点向右一步
            Pop(S,p);
            if(!Visit(p->data)) return ERROR;
            Push(S,p->rchild);
        }
    }
    return OK;
}

//二叉链表的中序遍历
//借助栈,非递归
Status InOrderTraverse(BiTree T,Status(* Visit)(TElemType e)){
    InitStack(S);   p=T;
    while(p||!StackEmpty(S)){
        if(p){              //根指针进栈，遍历左子树
            Push(S,p);  
            p = p->lchild;
        }
        else{               //根指针退栈访问根结点，遍历右子树
            Pop(S,p);
            if(!Visit(p->data)) return ERROR;
            p = p->rchild;
        }
    }
    return OK;
}

int main(){


    return 0;
}


/********************补充**********************/
//递归形式
//先序
void PreOrder(BiTree *bt){
    if(bt){
        visit(bt->data);
        PreOrder(bt->lchild);
        PreOrder(bt->rchild);
    }
}
//中序
void InOrder(BiTree *bt){
    if(bt){
        InOrder(bt->lchild);
        visit(bt->data);
        InOrder(bt->rchild);
    }
}
//后序
void PostOrder(BiTree *bt){
    if(bt){
        PostOrder(bt->lchild);
        PostOrder(bt->rchild);
        visit(bt->data);
    }
}

//层次遍历
/*
    利用一个队列，将根入队，以后队列不空取队头p
    p不空，访问，再将右子树入队。
*/
//queue
void LevelOrder(BiTree *bt){
    InitQueue(Q);           //初始化
    EnQueue(Q,bt);          //根入队
    while(!QueueEmpty(Q)){  //队列不为空
        DeQueue(Q,p);
        if(p!= NULL){
            visit(p->lchild);
            //左右子树入队
            EnQueue(Q,p->lchild);
            EnQueue(Q,p->rchild);
        }
    }
}
//队列表现为q[]+front+rear
void LevelOrder(BiTree *bt){
    const int maxn = 1024;
    BiTree q[maxn];
    int front,rear;
    //初始化为空
    front = rear = 0;
    //根入队列
    q[rear] = bt; rear = (rear+1) % maxn;
    //队列不为空
    while(front != rear){
        p = q[front];   front = (front+1) % maxn;
        if(p){
            visit(p->data);
            //左右子树入队列
            q[rear] = p->lchild;    rear = (rear+1) % maxn;
            q[rear] = p->rchild;    rear = (rear+1) % maxn;
        }

    }
}


//非递归
//中序
//沿着左子树向下移动，同时入栈保存。到达空子树就退栈访问结点，然后移动到右子树
void InOrder(BiTree *bt){
    InitStack(S);
    p = bt;
    while(p || !StackEmpty(S)){
        if(p){
            Push(S,p);
            p = p->lchild;
        }
        else{
            Pop(S,p);
            visit(p);
            p = p->rchild;
        }
    }
}
//先序
void PreOrder(BiTree *bt){
    InitStack(S);
    p = bt;
    while(p || !StackEmpty(S)){
        if(p){
            visit(p);       //先序访问结点的位置
            Push(S,p);
            p = p->lchild;
        }
        else{
            Pop(S,p);
            p = p->rchild;
        }
    }
}
//后序
//分别从左右子树返回根结点，只有从右子树的时候才访问根结点，所以增加一个栈标记到达结点的次序。
void PostOrder(BiTree *bt){
    InitStack(S);InitStack(tag);
    p = bt;
    while(p||!StackEmpty(S)){
        if(p){
            Push(S,p);  Push(tag,1);        //第一次入栈
            p = p->lchild;
        }
        else{
            Pop(S,p);   Pop(tag,f);
            if(f == 1){
                //左子树返回，二次入栈，p转右子树
                Push(S,p);  Push(tag,2);
                p = p->rchild;
            }
            else{
                //右子树返回，访问根结点，p转上层
                visit(p);
                p = NULL;       //下一步退栈
            }
        }
    }
}



/**************遍历二叉树的应用****************/

//二叉树结点的个数
int NodeCount(BiTree *bt){
    if(bt == NULL) return 0;
    else return 1+NodeCount(bt->lchild)+NodeCount(bt->rchild);
}

//二叉树叶子结点的个数
int LeafCount(BiTree *bt){
    if(bt == NULL) return 0;
    else if(bt->lchild == NULL && bt->rchild == NULL)   return 1;
    else return LeafCount(bt->lchild) + LeafCount(bt->rchild);
}

//二叉树的深度
int Depth(BiTree *bt){
    if(bt == NULL ) return 0;
    else return 1+max(Depth(bt->lchild),Depth(bt->rchild));
}

 

---

 

 

 

#include<bits/stdc++.h>
using namespace std;
#define INF 0xfffff
#define MAX_N 20
typedef enum {DG,DN,UDG,UDN} GraphKind; //{有向图，有向网，无向图，无向网}
bool visited[MAX_N];

/*基本操作

CreateGraph(&G,V,VR);       //构造图。V是顶点集，VR是弧
DestroyGraph(&G);           //销毁图
LocateVex(G,u);             //返回顶点u的位置
GetVex(G,v);                //返回v的值
PutVex(&G,v,value);         //对v赋值value
FirstAdjVex(G,v);           //返回v的第一个邻接顶点
NextAdjVex(G,v,w);          //返回v的下一个邻接顶点（相对于w）
InsertVex(&G,v);            //在图中加入顶点
DeleteArc(&G,v);            //删除v及v相关的弧
InsertVex(&G,v,w);          //加入v,w的弧
DeleteVex(&G,v,w);          //在G中删除弧v,w
DFSTraverse(G,Visit());     //DFS
BFSTraverse(G,Visit());     //BFS

*/


typedef struct ArcCell{
    VRType adj;         //顶点关系类型。无权图0/1
    InfoType *info;     //该弧相关信息的指针

}ArcCell,AdjMatrix[MAX_N][MAX_N];

typedef struct{
    VertexType vexs[MAX_N];     //顶点向量
    AdjMatrix arcs;             //邻接矩阵
    int vexnum,arcnum;          //图的当前顶点数和弧数
    GraphKind kind;             //图的种类
}MGraph;

//邻接表
typedef struct ArcNode{
    int adjvex;                 //弧所指向顶点的位置
    struct ArcNode *nextarc;    //指向下一条弧的指针
    InfoType *info;             //该弧的相关信息的指针
}ArcNode;

typedef struct VNode{   
    VertexType data;            //顶点信息
    ArcNode *firstarc;          //指向第一条依附该顶点的弧的指针
}VNode,AdjList[MAX_N];
typedef struct{
    AdjList Verices;            
    int vexnum,arcnum;          //当前顶点数和弧数
    int kind;                   //图种类标志
}ALGraph;


//DFS
Status (*VisitFunc)(int v);
void DFSTraverse(Graph G,Status (*Visit)(int v)){
    VisitFunc = Visit;          //使用全局变量
    for(v = 0; v < G.vexnum; v++)   visited[v] = FALSE;    //访问标志数组初始化
    for(v = 0; v < G.vexnum; v++){
        if(!visited[v]) DFS(G,v);       //对尚未访问的邻接点调用DFS
    }  
}

void DFS(Graph G, int v){
    //从第v个结点出发访问
    visited[v] = TRUE; VisitFunc(v);    //访问第v个顶点
    for(w = FirstAdjVex(G,v); w>=0 ; w = NextAdjVex(G,v,w))
        if(!visited[w]) DFS(G,w);       //对v尚未访问的顶点w递归调用DFS
}

//BFS
void BFSTraverse(Graph G,Status (*Visit)(int v)){
    for(v = 0 ; v < G.vexnum; v++)  visited[v] = FALSE;
    InitQueue(Q);
    for(v = 0; v < G.vexnum; v++){
        if(!visited[v]){                    //v尚未访问
            visited[v] = TRUE;  Visit(v);   
            EnQueue(Q,v);                   //v入队
            while(!QueueEmpty(Q)){
                DeQueue(Q,u);               //队头出队并置为u
                for(w = FirstAdjVex(G,u);w >= 0; w = NextAdjVex(G,u,w)){
                    if(!visited[w] = TRUE){ //w为u的尚未访问过的邻接顶点
                        visited[w] = TRUE; Visit(w);
                        EnQueue(Q,w);
                    }
                }
            }
        }
    }
}


//Prim
Void Prim(MGraph G, VertexType u){
    /*
    struct{
        VertexTypeadjvex;
        VRType lowcost;
    }closedge[MAX_N];
    */
    k = LocateVex(G,u);
    //辅助数组初始化
    for(j = 0 ; j < G.vexnum; i++){         
        if(j != k ) closedge[j] = {u,G.arcs[k][j].adj};
    }
    closedge[k].lowcost = 0;                    //初始U={u}
    for(i = 1; i < G.vexnum; i++){              //选择其余G.vexnum-1个结点
        k = minimum(closedge);                  //求出T的下一个结点，k
        /*此时
        closedge[k].lowcost =
            min{closedge[vi].lowcost|closedge[vi].lowcost>0}
        */

        printf(closedge[k].adjvex,G.vexs[k]);   //输出生成树的边
        closedge[k].lowcost = 0;                //第k个顶点入U
        for(j = 0; j < G.vexnum; j++){
            if(G.arcs[k][j].adj < closedge[j].lowcost){//新顶点入U后重新选择最小边
                closedge[j] = {G.vexs[k],G.arcs[k][j].adj};
            }
        }
    }
}


int main(){

    return 0;
}

 

---

 

 

 

 

 

 

  

#include<bits/stdc++.h>
using namespace std;

typedef float KeyType;
typedef int KeyType;
typedef char *KeyType;

#define EQ(a,b) (a == b)
#define LT(a,b) (a < b)
#define LQ(a,b) (a <= b)


typedef struct{
    KeyType key;    //关键字
    ......          //其他

}SElemType；


/*基本操作
Create(&ST,n);      //构造一个含n个数据元素的集合ST
Destroy(&ST);       //销毁ST
Search(ST,key);     //查找和key相等的元素，并返回位置
Traverse(ST,Visit); //按照某种次序对每个元素调用函数，仅一次
*/


//顺序
typedef struct {
    TElemType *elem;        //数据元素存储空间基址
    int length;             //表长度
}SSTable;   

 //顺序查找
 int Search_Seq(SSTable ST,KeyType key){
    ST.elem[0].key = key;   //哨兵
    for(i = ST.length; !EQ(ST.elem[i].key,key); --i)    //从后往前找
        return i;

 }

 //折半查找
 int Search_Bin(SSTable ST,KeyType key){
    low = 1;    high = ST.length;       //置区间初值
    while(low <= high){ 
        mid = (low + high) / 2;
        if(EQ(key,ST.elem[mid].key))    return mid; //找到
        else if(LT(key,ST.elem[mid].key))   high = mid - 1; // 前半区间
        else    low = mid + 1;          //后半区间

    }
    return 0; 
 }

/*****************动态查找*****************/
/*基本操作

InitDSTable(&DT);               //创造空的动态表
DestroyDSTable(&DT);            //销毁动态表
SearchDSTable(DT,key);          //查找和key相等的数据元素返回位置   
InsertDSTable(&DT,e);           //不存在和e.key相等的元素的情况下插入e
DeleteDSTable(&DT,e);           //若存在和e.key相等的元素，删除。
TraverseDSTable(DT,Visit());    //对DT每个结点只访问一次

*/


//二叉排序树
 //查找
 BiTree SearchBST(BiTree T, KeyType key){
    //根指针T所指二叉排序树中递归的查找某关键字等于key的数据元素。
    //查找成功，返回指向该数据元素结点的指针。
    if(!T || EQ(key,T->data.key))   return T;
    else if(LT(key,T->data.key))    return (SearchBST(T->lchild,key));  
    else return (SearchBST(T->rchild,key));
 }
 
 //查找便于插入版本
 Status SearchBST(BiTree T,KeyType key,BiTree f,BiTree &p){
    if(!T)  {p = f; return FALSE;}
    else if(EQ(key,T->data.key))    {p = T; return TRUE;}
    else if(LT(key,T->data.key))    return  SearchBST(T->lchild,key,T,p);
    else return SearchBST(T->rchild,key,T,p);
}
 //插入
Status InsertBST(BiTree &T,ElemType e){
    if(!SearchBST(T,e.key,NULL,p)){
        s = (BiTree) malloc(sizeof(BiTNode));
        s->data = e; s->lchild = s->rchild = NULL;          
        if(!p)  T = s;                                      //被插结点为新的根结点。
        else if LT(e.key,p->data.key)  p->rchild = NULL;    //被插结点为左孩子
        else p->rchild = s;                                 //被插结点为右孩子
        return TRUE;
    }
    else    return FALSE;
}

//删除
Status DeleteBST(BiTree &T,KeyType key){
    if(!T)  return FALSE;
    else{
        if(EQ(key,T->data.key)) return Delete(T);
        else if(LT(key,T->data.key))    return DeleteBST(T->lchild,key);
        else return DeleteBST(T->rchild,key);
    }
}
Status Delete(BiTree &p){
    //重连左/右子树
    //右子树空就重连左子树
    if(!p->rchild){
        q = p;
        p = p->lchild;
        free(q);
    }
    else if(!p->lchild){        //重连右子树
        q = p;
        p = p->rchild;
        free(q);
    }
    else{                       //左右子树都不空
        q = p;  s = p->lchild;
        while (s->rchild){q = s; s = s->rchild;} //转左，向右到尽头
        p->data = s->data;                  //s指向被删结点的前驱
        if(q != p)  q->rchild = s->lchild;  //重连右子树
        else    q->lchild = s->lchild;      //重连左子树
        delete s;
    }
    return TRUE;
}

int main(){


    return 0;
}

 

---

 

 

 

 

 

 

 

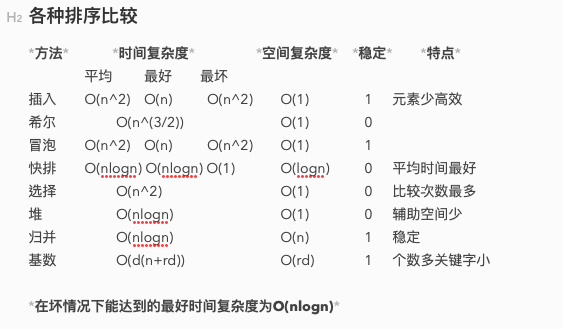
#include<bits/stdc++.h>
using namespace std;

#define maxn 20
typedef int KeyType;

typedef struct {
    KeyType key;            //关键字项
    InfoType otherinfo;     //其他数据项
}RedType;

typedef struct {
    RedType r[maxn+1];
    int length;
}SqList;

//LT(a,b) <=> a<b

//直接插入排序
void BinInsert(SqList &L){
    for(i = 2 ; i <= L.length; i++){    
        if(LT(L.r[i].key, L.r[i-1].key)){     //<,L.r[i]插入有序子表
            L.r[0] = L.r[i];                  //复制为哨兵
            L.r[i] = L.r[i-1];
            for(j = i-2; LT(L.r[0].key,L.r[j].key); --j){
                L.r[j+1] = L.r[j];            //记录后移
            }
            L.r[j+1] = L.r[0];                //插入到正确位置
        }
    }
}

//折半插入排序
void BInsertSort(SqList &L){
    for(i = 2; i <= L.length ;i++){
        L.r[0] = L.r[i];                //暂存到L.r[0]
        low = 1; high = i-1;
        while(low <= high){             //在low-high中折半查找有序
            m = (low + high)/2;         //折半
            if(LT(L.r[0].key,L.r[m].key))   high = m-1;     //插入点在低半区
            else    low = m+1;                              //插入点在高半区
        }
        for(j = i-1 ;j >= high+1 ; j--) L.r[j+1] = L.r[j];  //记录后移

        L.r[high+1] = L.r[0];           //插入
    }
}

//希尔排序
void ShellInsert(SqList &L,int dk){
    for(i = dk+1 ; i <= L.length; i++){
        if(LT(L.r[i].key, L.r[i-dk].key)){  //将L.r[i]插入有序子表
            L.r[0] = L.r[i];                //暂存在L.r[0]
            for(j = i-dk ; j > 0 && LT(L.r[0].key,L.r[j].key); j -= dk){
                L.r[j+dk] = L.r[j];         //记录后移，查找插入位置
            }
            L.r[j+dk] = L.r[0];
        }
    }   
}
void ShellSort(SqList &L,int dita[],int t){
    for(k = 0; k < t; k++){
        ShellInsert(L.dlta[k]);     //一趟增量为dlta[k]的插入排序
    }
}

//快速排序
int Partition(SqList &L,int low,int high){
    L.r[0] = L.r[low];          //用子表的第一个记录作枢轴
    pivotkey = L.r[low].key;    //枢轴记录关键字
    while(low < high){          //从表的两端交替向中间扫描
        while(low < high && (L.r[high].key >= pivotkey) ) --high;
        L.r[low] = L.r[high];   //小的移到低端
        while(low < high && (L.r[high].key <= pivotkey) ) ++low;
        L.r[high] = L.r[low];   //大的移到高端
    }
    L.r[low] = L.r[0];          //枢轴记录到位
    return low;                 //返回枢轴位置
}
void QSort(SqList &L, int low ,int high){
    if(low < high){
        pivotloc = Partition(L,low,high);   //分成两个子表
        QSort(L,low,pivotloc-1);            //低子表递归排序               
        QSort(L,pivotloc+1,high);           //高子表递归排序
    }   
}
void QuickSort(SqList &L){
    QSort(L,1,length);
}

//简单选择排序
void SelectSort(SqList &L){
    for(i = 1; i < L.length ;i++){
        j = SelectMinKey(L,i);
        if(i != j)  swap(L.r[i],L.r[j]);
    }
}

//归并排序
void Merge(T a[],int low,int mid,int high){
    i = low;
    j = mid+1;  k = low;
    while(i <= mid && j <= high){
        if(a[i] <= a[j]){
            b[k] = a[i];
            i++;
        }
        else{
            b[k] = a[j];
            j++;
        }
        k++;
    }
    while(i <= mid) b[k++] = a[i++];
    while(j <= high)    b[k++] = a[j++];
    a[low...high] = b[low...high];       
}
void MergeSort(T a[],int low ,int high){
    if(low >= high) return;
    else{
        int mid = (low+high)/2;
        MergeSort(a,low,mid);
        MergeSort(a,mid+1,high);
        Merge(a,low,mid,high);
    }
}


int main(){
    
    return 0;
}

 

---

 

 

#include<bits/stdc++.h>
using namespace std;
#define MaxSize 255

typedef unsigned char SString[MaxSize + 1];
/*基本操作
    StrAssign(&T,chars);        //生成一个值等于chars的串T
    StrCopy(&T,S);                //由串S复制得T
    StrEmpty(S);                //判断串是否为空
    StrCompare(S,T);            //S > T 返回>0
    StrLength(S);                //返回S的元素个数，串的长度
    ClearString(&S);            //清空S
    Concat(&T,S1,S2);            //返回由S1，S2连接而成的新串
    SubString(&Sub,S,pos,len);    //Sub返回串的第pos个字符起长度为len的子串
    Index(S,T,pos);                //返回T在S中第pos个字符后第一次出现的位置
    Replace(&S,T,V);            //用V替换S中所有与T相等的不重叠子串
    StrInsert(&S,pos,T);        //在S的第pos个字符前插入串T
    StrDelete(&S,pos,len);        //删除第pos个字符开始长度为len的子串
    DestroyString(&S);            //串被销毁

 */


//模式匹配
int Index(SString S,SString T, int pos){
    i = pos; j = 1;
    while(i <= S[0] && j <= T[0]){
        if(S[i] == S[T]){
            ++i;    ++j;        //继续比较后继字符
        }
        else{
            i = i-j+2; j = 1;    //指针后退重新匹配
        }
    }
    if(j > T[0])    return i-T[0];
    else return 0;
}

//KMP
int Index_KMP(SString S,SString T,int pos){
    i = pos;    j = 1;
    while(i <= S[0] && j <= T[0]){
        if(j == 0 || S[i] == T[j]){
            ++i; ++j;                    //继续比较后继字符
        }
        else    j = next[j];            //模式串向右移动
    }
    if(j > T[0])    return i-T[0];        //匹配成功    
    else return 0;                        
}

//next数组
void get_next(SString T,int next[]){
    i = 1; next[1] = 0; j = 0;
    while(i < T[0]){
        if(j == 0 || T[i] == T[j]){
            ++i; ++j; next[i] = j;
        }
        else    j = next[j];
    }
}

//nextval
void get_nextval(SString T ,int nextval[]){
    i = 1;nextval[1] = 0; j = 0;
    while(i < T[0]){
        if(j == 0 || T[i] == T[j]){
            ++i; ++j;
            if(T[i] != T[j])    nextval[i] = j;
            else    nextval[i] = nextval[j];
        }
        else    j = nextval[j];
    }
}
int main(){
    

    return 0;
}