DDCA —— SIMD结构和向量处理器

1. SIMD 处理：利用常规（数据） 并行性

1.1 数据级并行的兴起与SIMD的优势

动机（Data Level Parallelism，DLP）：

  • 应用需求和技术发展推动着体系结构的发展
  • 图形、机器视觉、语音识别、机器学习等新的应用均需要大量的数值计算，其算法通常具有数据并行特征
  • SIMD-based结构（vector-SIMD，SIMD/GPUs）是执行这些算法的最有效途径

SIMD 结构可有效地挖掘数据级并行：

  • 基于矩阵运算的科学计算

  • 图像和声音处理

  • ......

SIMD 比 MIMD 更节能

  • 针对每组数组操作仅需取指一次

SIMD 允许程序员继续以串行模式思考

1.2 SIMD 发展

三种变体：

  • 向量体系结构

  • SIMD/Multimedia 指令级扩展

  • Graphics Processor Units (GPUs)

对于X86处理器：

  • MIMD 每年增加2 cores/chip

  • SIMD 宽度每 4 年翻一番

  • SIMD 潜在加速比是 MIMD 的2倍

image-20241216155116391

1.3 Flynn 计算机分类法

  1. SISD: Single instruction operates on single data element（单指令流单数据流）
  • 单一指令操作单一数据元素
  1. SIMD：Single instruction operates on multiple data elements（单指令流多数据流）
  • 单一指令操作多个数据元素
  • 阵列处理器（Array Processor）：多个处理单元并行操作不同的数据
  • 向量处理器（Vector Processor）：执行向量化操作，常见于科学计算和图形处理
  1. MISD：Multiple instructions operate on single data element（多指令流单数据流）
  • 多条指令操作同一个数据元素
  • 接近形式：
    • 脉动阵列处理器（Systolic Array Processor）：数据在多个处理单元之间传递，指令并行执行
    • 流处理器（Streaming Processor）：例如在信号处理和数据流计算中用于连续操作同一数据
  1. MIMD：Multiple instructions operate on multiple data elements (multiple instruction streams) （多指令流多数据流）
  • 多条指令操作多个数据元素（即多个指令流）
  • 多处理器（Multiprocessor）：例如多核CPU，每个核心可以执行不同的任务
  • 多线程处理器（Multithreaded Processor）：例如支持多线程并发执行的现代处理器

1.4 数据并行性（Data Parallelism）

  1. 并发性源于在不同的数据块上执行相同的操作
  • 单指令多数据 (SIMD)
  • 例如：两个向量的点积操作
  1. 与数据流并行的对比
  • 并发性源于以数据驱动的方式并行执行不同的操作。
  1. 与线程并行的对比
  • 并发性源于并行执行不同的控制线程。
  1. SIMD 利用操作级并行性 (Operation-Level Parallelism, OLP) 来处理不同的数据
  • 相同的操作被并行地应用于不同的数据块上。
  • 这是一种指令级并行性 (ILP)，但指令在不同数据块上是相同的。

1.5 SIMD 处理范式（SIMD Processing Paradigm）

  1. 单条指令作用于多个数据元素
  • 在时间上或空间上实现
  1. 多个处理单元 (PEs, Processing Elements)
  • 即多个执行单元
  1. 时空结合的实现方式：
  • 阵列处理器 (Array Processor)：
    单条指令在相同时间内，通过不同的空间（多个处理单元，PEs）操作多个数据元素。
  • 向量处理器 (Vector Processor)：
    单条指令在连续的时间步骤内，通过相同的空间（同一个处理单元，PE）操作多个数据元素。
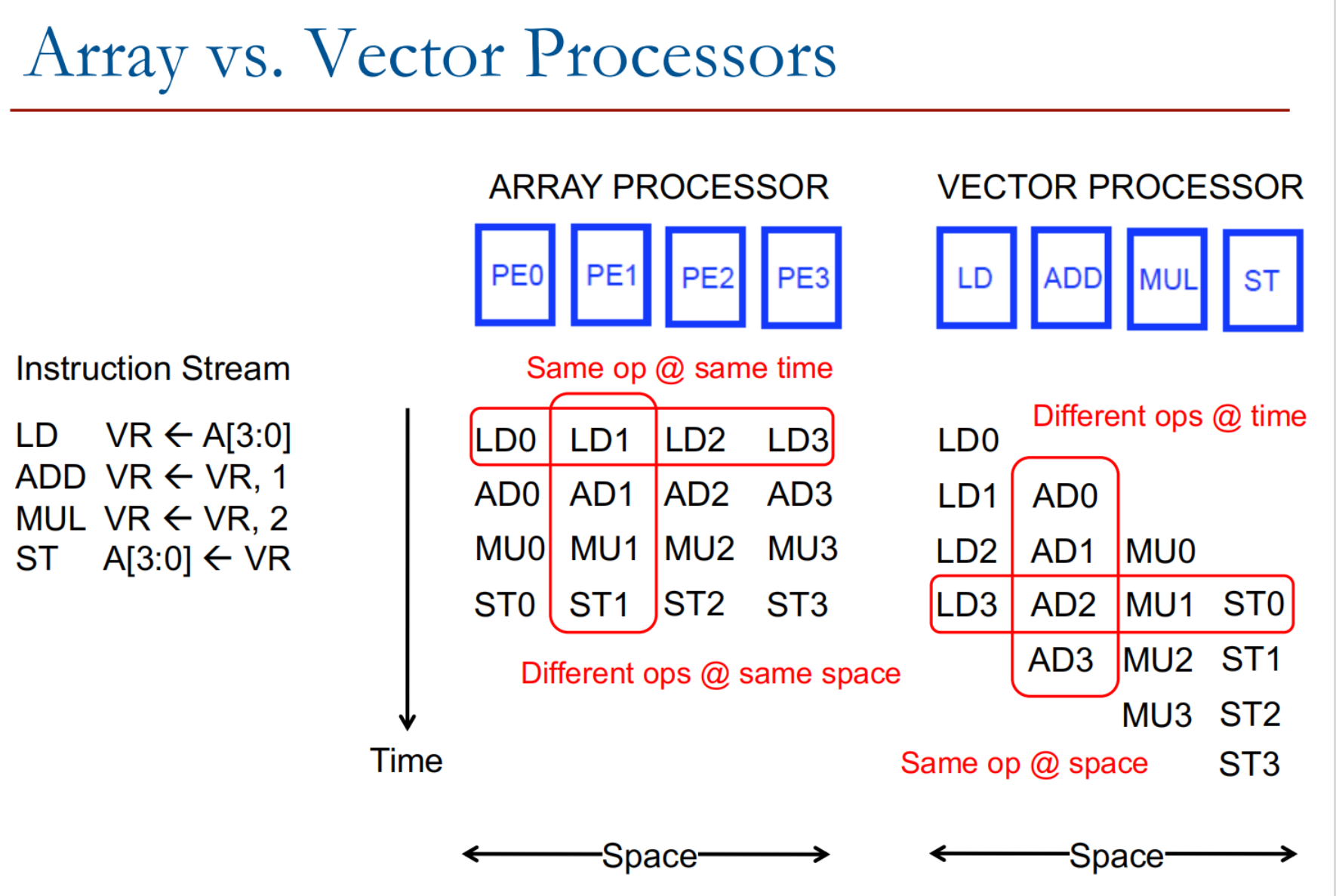
image-20241219212816192

如上图所示：

  1. 阵列处理器

    阵列处理器有多个处理单元（PE0、PE1、PE2、PE3），每个单元独立处理一部分数据。

    相同操作同时执行（SIMD: Single Instruction Multiple Data） 阵列处理器的每个处理单元同时执行相同的操作，但作用在不同的数据元素上：

    • 第一行：LD0, LD1, LD2, LD3 同时完成数据加载。

    • 第二行：AD0, AD1, AD2, AD3 同时完成加法操作。

    • 第三行：MU0, MU1, MU2, MU3 同时完成乘法操作。

    • 第四行：ST0, ST1, ST2, ST3 同时完成数据存储。

    时间维度：同一时刻，各个 PE 执行相同的指令。

    空间维度：不同 PE 处理不同的数据。

  2. 向量处理器

    向量处理器中，每个处理单元的功能不同，分别负责加载（LD）、加法（ADD）、乘法（MUL）和存储（ST）。

    时间维度： 同一时刻，各个 PE 执行不同的指令。

    空间维度： 同一 PE 执行相同的功能。

1.6 存储多个数据元素：向量寄存器

每个向量数据寄存器存储 N 个 M 位值

  • 每个寄存器存储一个向量
  • 不再是之前看到的 （单个）标量值
  • 这样就能实现流水线
image-20241219220005085

1.7 SIMD 阵列处理器 vs. VLIW

VLIW（超长指令字）：将多个独立操作打包在一起组成一个“长指令”

  • 指令之间是相互独立的，可以有不同的操作
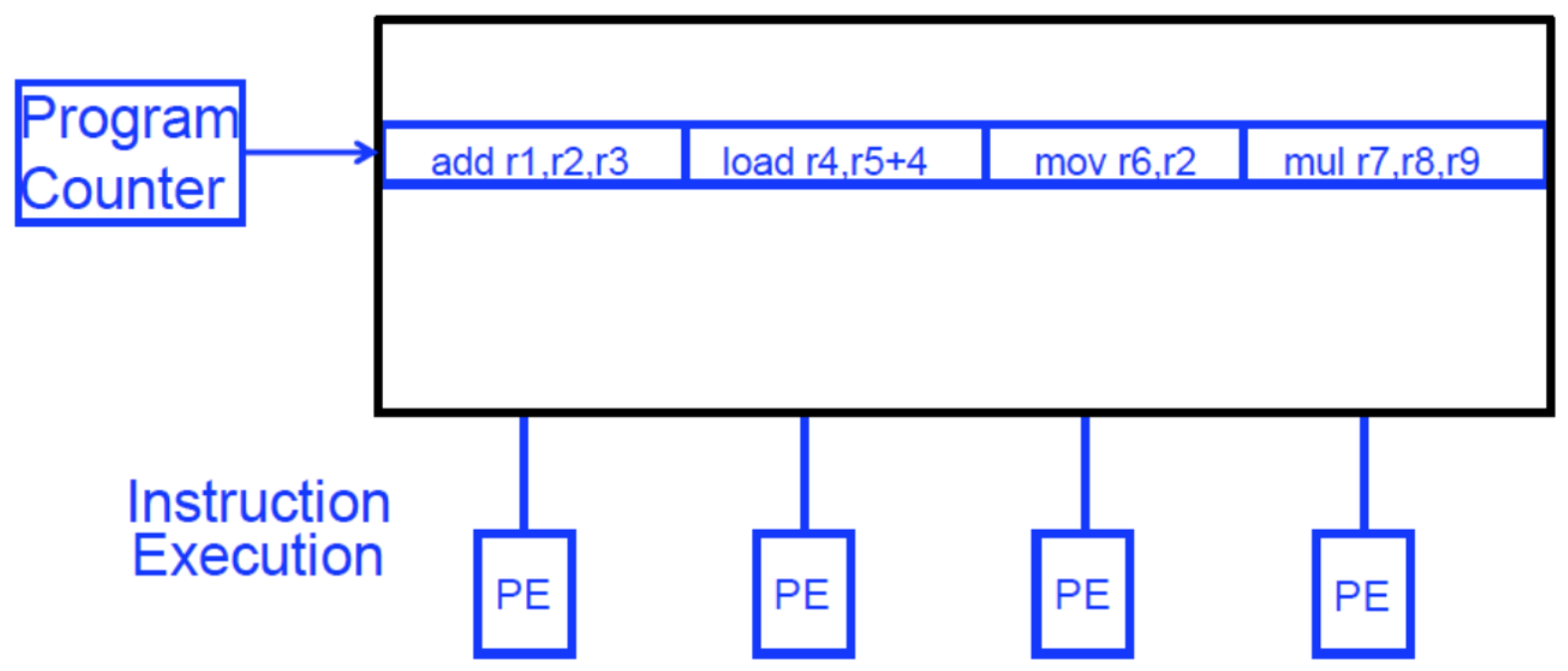
image-20241219221743330

阵列处理器：对多个（不同的）数据元素执行单一操作

image-20241219222034936

1.8 向量处理器的基本特性

基本思想：

  • 向量运算：
    • 向量处理器的核心思想是对两个向量的对应分量进行运算，最终生成一个结果向量。
    • 例如：对向量A和向量B的各元素进行加法运算，得出结果向量C。
    • 这种操作天然具有并行性，非常适合硬件流水线处理。
  • 减少指令获取次数：
    • 一条向量指令可以包含多个操作，例如对整个向量的每个元素进行加法运算。
    • 与标量处理器相比，这样的设计可以减少指令提取的次数，从而提高效率。

结果独立性：

  • 长流水线设计：向量处理器通过长流水线来加速运算，流水线中每个阶段可以独立完成一个操作。
  • 编译器保证无数据相关性：编译器需要确保向量指令中的操作彼此独立，避免操作间的依赖问题（如写后读冲突）。
  • 硬件相关性检测：硬件只需要检测不同向量指令之间是否存在依赖关系（而不是每个向量分量之间），大大简化了控制逻辑。
  • 较高的时钟频率：由于流水线中没有过多的数据相关性检查，可以实现更高的时钟频率，提高计算效率。

存储器访问模式：

  • 已知模式的存储器访问：
    • 向量指令会以固定模式访问存储器。例如，按顺序访问存储器地址中连续的数据。
    • 这种模式化的访问减少了复杂的地址计算开销。
  • 多体交叉存储器（Interleaved Memory）：向量处理器能够充分利用多体交叉存储器的特性，使不同的向量分量并行存取，从而提高内存带宽。
  • 减少对数据缓存的需求：由于向量数据可以按照固定的模式从内存加载，向量处理器通常只需使用指令缓存而不需要复杂的数据缓存，进一步降低硬件设计复杂性。

流水线控制的优化

  • 减少控制Hazard：由于向量处理器的流水线设计较为简单，且向量指令间的独立性强，可以有效减少控制冒险（control hazard）的发生。
  • 高效利用流水线并发：向量处理器可以充分发挥流水线的并发能力，使得不同的向量操作阶段可以同时进行，提高指令执行效率。

1.9 向量处理模型

向量处理器具有更高层次的操作，一条向量指令可以同时处理N个或N对操作数（处理对象是向量）

image-20241219223755755

1.9.1 向量处理器-1

向量是一个一维的数字数组。

示例代码：这段代码通过遍历数组对每个元素进行操作，实际上是典型的向量运算。

for (i = 0; i <= 49; i++) {
    C[i] = (A[i] + B[i]) / 2;
}

向量处理器是一种指令直接对向量进行操作的处理器，而不是像标量处理器那样只能处理单个数据值。

基本需求：

  1. 需要加载/存储向量：向量寄存器（vector registers）专门用来存储向量数据。
  2. 需要支持不同长度的向量操作：向量长度寄存器（VLEN）用于指定向量的实际长度，从而支持不同长度的向量运算。
  3. 向量的元素可能在内存中不连续存储：向量步幅寄存器（VSTR）用于定义向量中两个相邻元素在内存中的距离。
  4. 步幅（Stride）：指内存中两个向量元素之间的距离。例如，如果步幅为 1，则向量元素在内存中是连续存储的；如果步幅为 2，则每两个向量元素之间间隔一个存储位置。

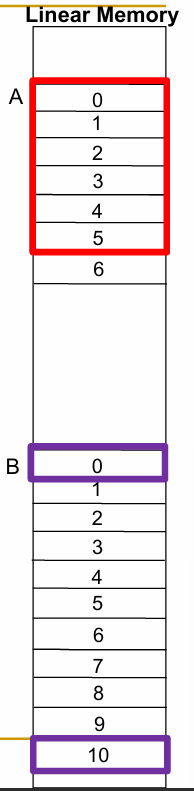
1.9.2 向量步幅示例：矩阵乘法

矩阵 A 和矩阵 B 的数据均以 行优先（row-major order） 存储在内存中。

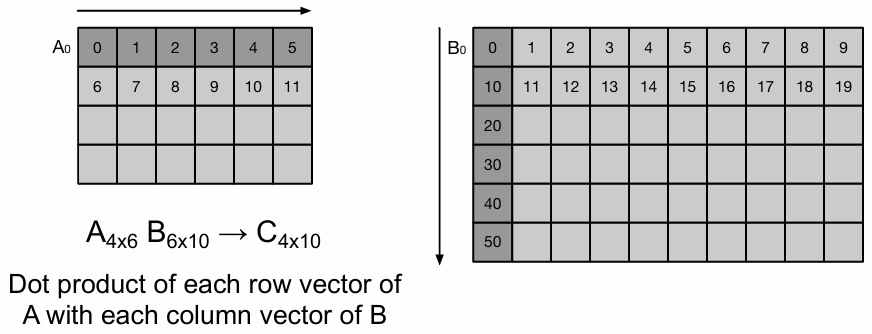
image-20241219225242044

加载 A 的第 0 行（A0 到 A5）到向量寄存器 V1：

  • 每次加载时，内存地址递增 1 来访问下一列的元素。
  • 这种访问的步幅（stride）是 1。

加载 B 的第 0 列（B0 到 B50）到向量寄存器 V2：

  • 每次加载时，内存地址递增 10 来访问下一行的元素。
  • 这种访问的步幅（stride）是 10。
image-20241219225406869

1.9.3 向量处理器-2

一条向量指令在连续的时钟周期中对向量中的每个元素执行操作。

  • 向量功能单元（functional units）是流水线化的。
  • 每个流水线阶段处理一个不同的数据元素。

向量指令支持更深的流水线设计：

  • 向量内部没有数据相关性：向量中元素的运算是相互独立的，因此硬件不需要额外的锁定机制来处理数据相关性。
  • 向量内部没有控制流：在处理单个向量时，不涉及条件分支等控制流操作。
  • 已知步幅（stride）：向量的存储位置是固定模式的（例如连续存储或有固定间隔），这使得可以轻松计算向量中所有元素的地址。
    • 这些特性使得向量的加载更加容易（甚至可以提前加载，即预取），并能将数据快速存储到寄存器、缓存或内存中。

1.10 向量处理器的优势

+ 向量内部没有数据相关性

  • 流水线和并行化可以非常高效地运行。
  • 可以设计非常深的流水线，而不会因深流水线的开销（例如数据冒险、硬件锁定等）而受到显著影响。

+ 每条指令产生大量的工作（操作）

  • 减少了对指令获取带宽的需求。
  • 将指令获取和控制的开销分摊到大量的数据上。
    • 这带来了每次操作的高能效。

+ 不需要显式编写循环代码

  • 指令序列中分支（如循环跳转）更少。

+ 非常规则的内存访问模式

1.11 向量处理器的劣势

-- 仅在并行性是规则的情况下（数据/SIMD并行）工作良好

  • ++ 对规则的向量操作非常有效。
  • -- 如果并行性是不规则的，会非常低效。
  • -- 那如果要在一个链表中查找某个键值呢？（显然这种不规则任务无法高效利用向量处理器）

Fisher 在论文“Very Long Instruction Word architectures and the ELI-512”中提到：

  • VLIW 架构尝试解决向量处理器的问题：
    • 对于向量处理器，编译器或程序员必须让代码中的数据结构非常接近硬件内置的规则结构才能有效运行。
    • 这种调整本身非常困难。

1.12 Amdahl定律

Amdahl定律

  • f：程序中可并行化的部分

  • N：处理器的数量

    \[Speedup = \frac{1}{1 - f + \frac{f}{N}} \]

  • Amdahl，"单处理器方法在实现大规模计算能力中的有效性"，AFIPS 1967年

最大加速比受限于串行部分：串行瓶颈

所有并行计算机都会“受到”串行瓶颈的影响。

image-20241219232729698

1.13 向量处理器的局限性

内存（带宽）可能很容易成为瓶颈，尤其是在以下情况：

  1. 计算/内存操作平衡没有得到保持

    向量处理器的性能很大程度上取决于计算和内存访问的平衡。如果计算速度过快，而内存访问速度跟不上，处理器就会变得空闲，无法充分利用计算资源，导致效率下降。因此，程序的设计需要确保计算与内存操作之间的平衡。

  2. 数据没有适当映射到 memory banks

    向量处理器通常依赖于多个 Memory Banks 并行处理数据。如果数据没有合理地分布到不同的 Memory Banks，就可能导致内存访问冲突或带宽瓶颈。例如，多个计算任务可能会尝试访问相同的内存位置，从而造成等待和性能下降。因此，正确地映射数据到不同的 Memory Banks 是确保高效执行的关键。

2. 向量处理的更深层次探讨

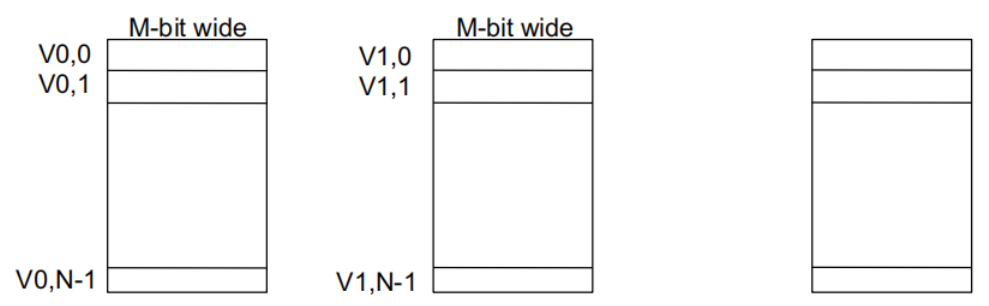
2.1 向量寄存器

每个向量数据寄存器包含 N 个 M 位的值

向量控制寄存器：VLEN、VSTR、VMASK

最大 VLEN 可以是 N

  • 向量寄存器中存储的最大元素数量

向量掩码寄存器（VMASK）

  • 指示需要操作的向量元素
  • 由向量测试指令设置
    • 例如：VMASK[i] = (Vk[i] == 0)
image-20241219233607809

2.2 向量功能单元

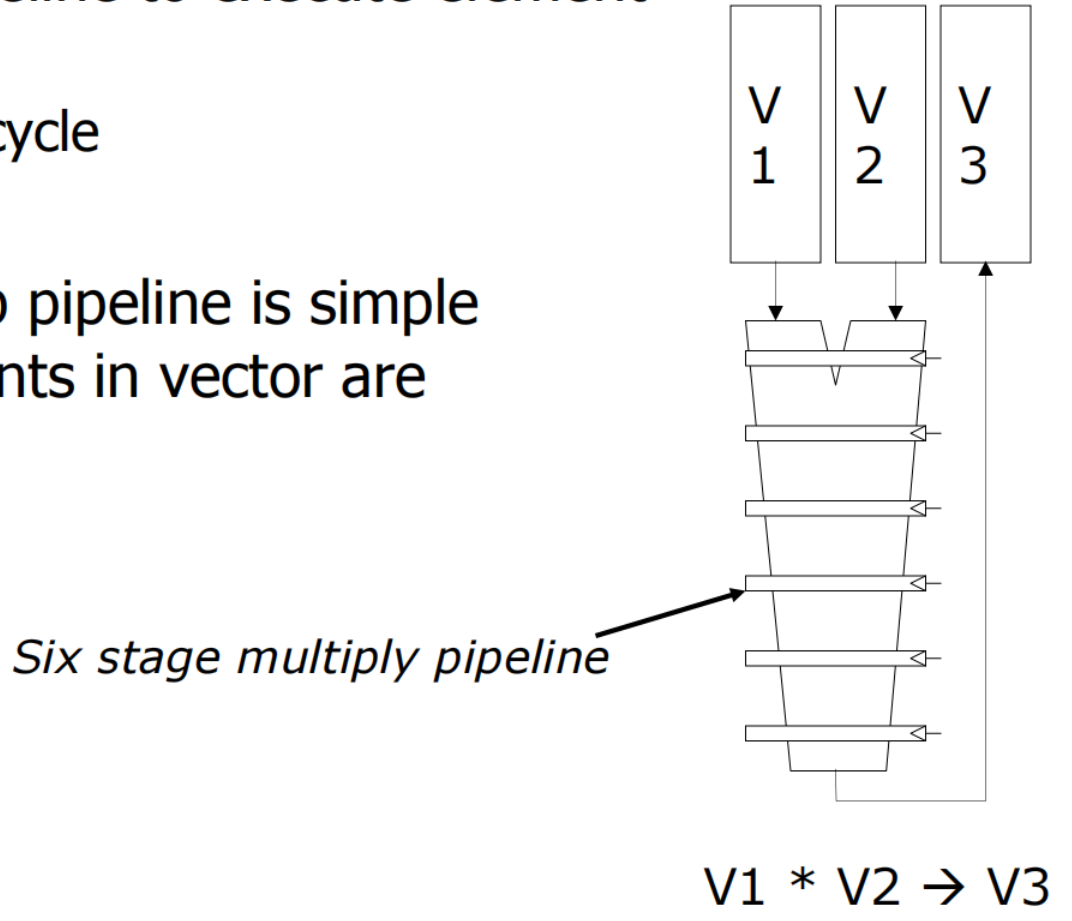
  1. 使用深流水线执行元素操作

    向量功能单元利用深度流水线（Deep Pipeline）来加速元素操作。深流水线指的是流水线有更多的阶段，这样可以使得每个时钟周期内能够执行更多的操作。

  2. 深流水线的控制相对简单，因为向量中的元素是独立的

image-20241219234941566

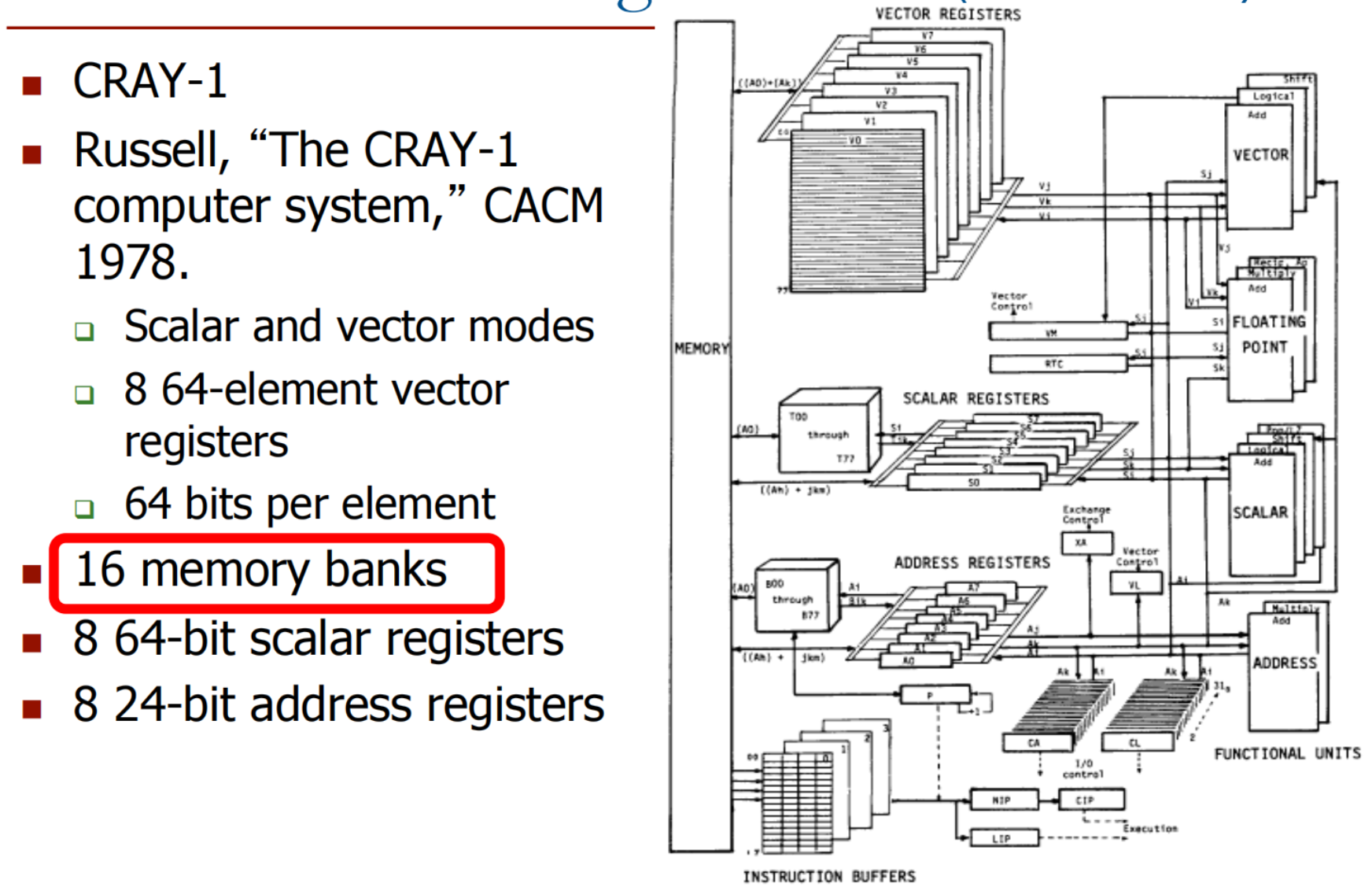
2.3 向量机组织（CRAY-1）

image-20241219235534521

2.3.1 从/向内存加载/存储向量

需要加载/存储多个元素

元素之间有固定的距离（步长）

  • 假设步长（stride）为1

如果每个周期可以启动一个元素的加载，那么元素可以在连续的周期内加载

  • 可以维持每个周期加载一个元素的吞吐量

问题：如何在内存访问需要多个周期的情况下实现这一点？

答案：将内存分成多个存储单元；将元素交错存储到不同的存储单元中

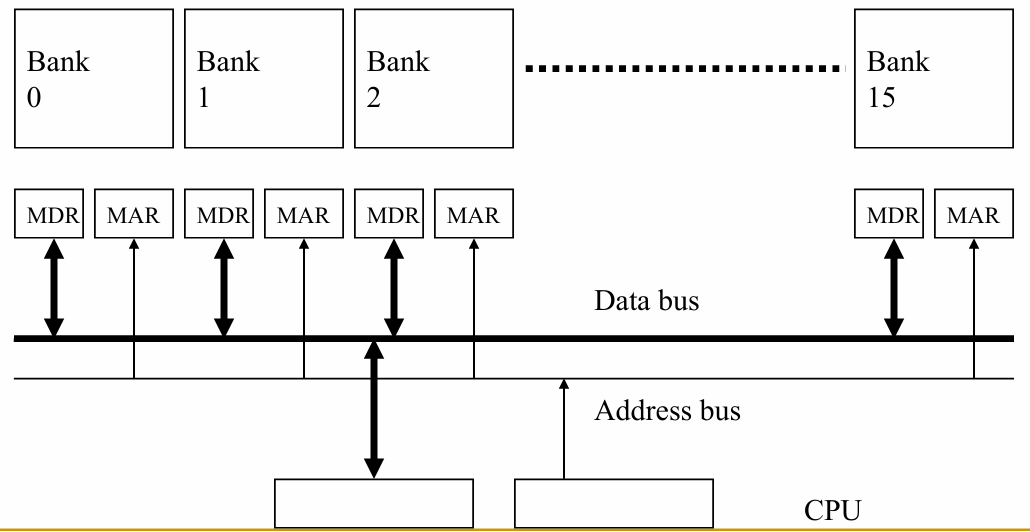
2.3.2 Memory Banking

内存被划分为多个独立的 bank；各 bank 共享地址总线和数据总线（以减少内存芯片的引脚数量）

每个周期可以启动并完成一个 bank 的访问

如果所有访问都指向不同的 bank，则可以持续进行 N 次并发访问

image-20241221162657737

2.3.4 向量内存系统

下一个地址 = 上一个地址 + 步幅（Stride）

如果（步幅 == 1）且（连续元素跨 memory bank 交错存储）且（memory bank 数量 ≥ memory bank 延迟），则：

  • 我们可以维持 1 元素/周期的吞吐量
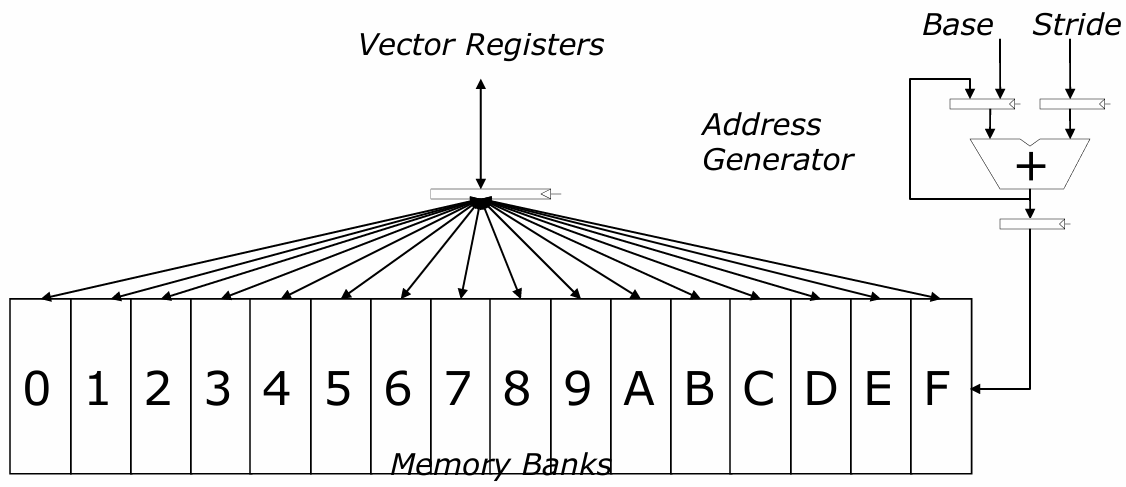
image-20241221162720955

2.4 标量 vs. 向量

2.4.1 标量代码示例：Element-Wise Avg.

for i = 0 to 49
	C[i] = (A[i] + B[i])/2

标量代码（指令及其在时钟周期中的延迟）：

	MOVI	R0 = 50			; 1 cycle
	MOVA	R1 = A			; 1 cycle
	MOVA 	R2 = B 			; 1 cycle
	MOVA	R3 = C			; 1 cycle
X:	LD		R4 = MEM[R1++]	; 11 cycle
	LD 		R5 = MEM[R2++]	; 11 cycle
	ADD		R6 = R4 + R5	; 4 cycle
	SHFR 	R7 = R6 >> 1	; 1 cycle
	ST		MEM[R3++] = R7	; 11 cycle
	DECBNZ	R0, X			; 2 cycle

该程序会执行 \(4 + 6 \times 50 = 300\) 条动态指令。

标量代码执行时间 （按顺序）：

在一个单存储体（bank）的顺序执行处理器上的标量执行时间

  • 循环中的前两个加载无法流水线化：\(2 \times 11\) 周期
  • \(4 + 50 \times 40 = 2004\) 周期

在一个具有两个存储端口（两个不同的内存访问可以同时进行服务）的单存储体顺序执行处理器上的标量执行时间，或者具有两个存储体（其中数组A和B存储在不同的存储体中）

  • 循环中的前两个加载可以流水线化：1 + 11周期
  • \(4 + 50 \times 30 = 1504\) 周期

2.4.2 向量化循环

可向量化的循环：

  • 如果每次迭代都是独立的，那么一个循环是可向量化的。
for i = 0 to 49
	C[i] = (A[i] + B[i])/2

向量化后的循环（每个指令及其延迟）：

MOVI		VLEN = 50 		; 1
MOVI 		VSTR = 1 		; 1
VLD 		V0 = A 			; 11 + VLEN - 1
VLD 		V1 = B 			; 11 + VLEN - 1
VADD 		V2 = V0 + V1 	; 4 + VLEN - 1
VSHFR 		V3 = V2 >> 1 	; 1 + VLEN - 1
VST 		C = V3 			; 11 + VLEN - 1

该程序会执行 7 条动态指令。

基本向量代码执行性能：

  • 假设没有链接（无向量数据转发）
    • 即，一个向量功能单元的输出不能直接被另一个用作输入
    • 整个向量寄存器需要准备好，其任何一个元素才能作为另一个操作的一部分
    • 这意味着必须等待整个向量操作完成，并且整个向量寄存器的内容都准备好了，之后才能开始下一个操作
  • 1 个 memory 端口（每个 memory bank 一个地址生成器）
  • 16个存储体（字交叉存储：数组的连续元素存储在连续的存储体中）
  • 总共需要285个周期
image-20241221162750283
  • 为什么是16个存储体？
    • 11个周期的内存访问延迟
    • 拥有16个（大于11）存储体可以确保有足够的存储体来重叠足够的内存操作以覆盖内存延迟
  • 上述假设单位步长（即，步长=1）
    • 对于我们的示例程序是正确的
  • 如果步长> 1会怎样？
    • 当内存延迟为11个周期时，如何确保我们每个周期可以访问一个元素？

2.5 向量链接（Vector Chaining）

向量链接：向量链接是指数据从一个向量功能单元转发到另一个单元的过程。

链接过程：

  • 加载单元从内存加载数据到v1。
  • 乘法单元（Mult.）接收来自v1的数据并与v2的数据相乘。由于向量链接的存在，v1的部分结果可以在准备好后立即被乘法单元使用，而无需等待整个v1向量。
  • 同样，v3的部分结果可以被加法单元（Add）立即使用，无需等待整个乘法操作完成。
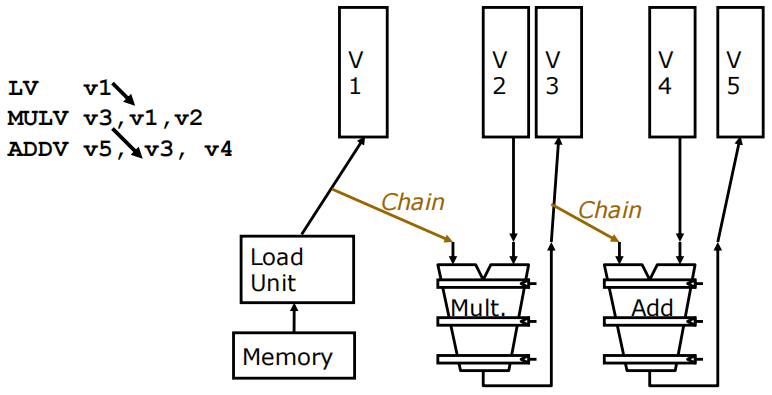
image-20241221163735211

对于 2.4.2节 的向量化程序：

  • VLD V0=A 和 VLD V1=B：这两个加载操作（VLD）不能流水线化。原因是每个存储体只有一个端口，导致内存带宽成为瓶颈，所以不能同时进行多个内存访问。
  • VADD 和 VSHFR：VADD（向量加法）和 VSHFR（向量右移）可以通过链接快速转发数据，减少了等待时间。
  • VLD 和 VST 不能流水线化：加载（VLD）和存储（VST）操作由于同样的内存端口限制，不能同时进行。
  • 总耗时：182个周期
image-20241221165044181

2.6 多个内存端口

如果每个 memory bank 有 2 个加载端口和 1 个存储端口。

  • VLD V0=A 和 VLD V1=B：由于有两个加载端口，这两个加载操作可以并行进行，从而加速内存访问。
  • VADD 和 VSHFR：向量加法（VADD）和向量右移（VSHFR）通过链式处理快速传递数据，进一步减少了执行时间。
  • 总耗时：79个周期
  • 性能提升：19倍
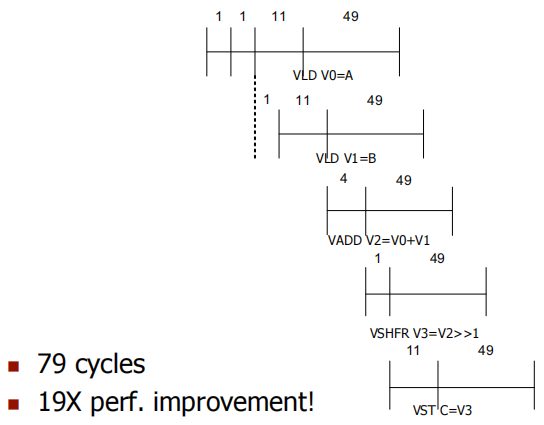
image-20241221165635494

2.7 Questions-1

如果数据元素数 > 向量寄存器中的元素数怎么办？

  • 想法：将循环分解，使每次迭代处理向量寄存器中的元素数量。
  • 例如，有527个数据元素，64个元素的向量寄存器（VREGs）。
  • 需要进行8次迭代，每次处理64个元素。
  • 最后一次迭代需要处理剩余的15个元素（需要改变向量长度VLEN的值）。
  • 这种方法被称为向量条带挖掘（vector stripmining）。

2.8 Questions-2

如果向量数据在内存中不是以固定步长存储的呢？（即不规则内存访问）

  • 想法： 使用间接寻址将元素组合/打包到向量寄存器中。
  • 这种技术称为散射/聚集（scatter/gather）操作。
  • 这样做还可以避免在稀疏向量（即许多元素为0的向量）上进行无用计算。

2.9 散射/聚集（scatter/gather）操作

向量化具有间接访问的循环，如：

for (i=0; i<N; i++)
    A[i] = B[i] + C[D[i]]

索引加载指令（聚集）：

LV 		vD, rD		; 加载D向量的索引
LVI 	vC, rC, vD	; 从rC基址间接加载到vC中
LV 		vB, rB		; 加载B向量
ADDV.D 	vA, vB, vC	; 执行加法操作
SV 		vA, rA		; 存储结果

聚集操作用于从非连续内存地址收集数据。这里，通过LVI指令，使用向量D中的索引来间接访问C向量，即从C的不同位置加载数据。

聚集/散射操作通常在硬件中实现，以处理稀疏向量（矩阵）或间接索引。

向量加载和存储使用一个索引向量，通过将其加到基址寄存器来生成地址。

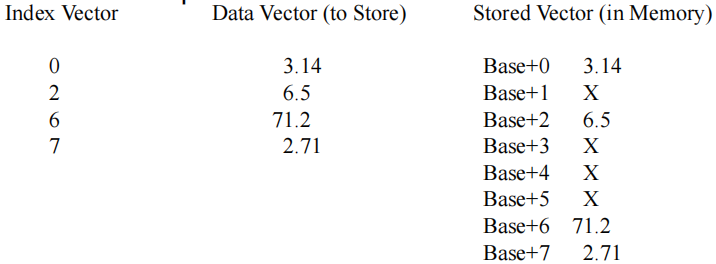
散射示例：

  • 索引向量 (Index Vector)： 指定数据应该存储的位置。
  • 数据向量 (Data Vector to Store)： 要存储的数据。
  • 存储向量 (Stored Vector in Memory)： 结果在内存中的存储情况。

索引向量包含位置索引 {0, 2, 6, 7}。

数据向量包含要存储的数据 {3.14, 6.5, 71.2, 2.71}。

在存储操作中，3.14 被存储在 基址+0 的位置，6.5 在 基址+2 的位置，71.2 在 基址+6 的位置，2.71 在 基址+7 的位置。

其他位置保留为X，表示这些位置没有被当前操作修改。

image-20241221181921116

2.10 Questions-3

如果某些操作不应在向量上执行怎么办？（基于动态确定的条件）

for (i=0; i<N; i++)
    if (a[i] != 0) 
        b[i] = a[i] * b[i];

在这个循环中，只有当a[i]不为零时，才执行乘法操作。

想法：掩码操作（Masked Operations）：

  • VMASK寄存器：这是一个位掩码，用于确定哪些数据元素不应被操作。
  • 执行步骤：
    • VLD V0 = A：将向量A加载到寄存器V0。
    • VLD V1 = B：将向量B加载到寄存器V1。
    • VMASK = (V0 != 0)：创建一个掩码，V0中不为零的元素对应的掩码位置为1。
    • VMUL V1 = V0 * V1：对V0和V1中的元素进行乘法操作，但仅对掩码为1的索引执行。
    • VST B = V1：将结果存储回向量B中。

举例：

循环逻辑：这个循环的目标是将a[i]或b[i]中较大的值存储到c[i]。

for （i = 0； i < 64; ++i）
    if (a[i] >= b[i])
        c[i] = a[i]
    else
        c[i] = b[i]

执行步骤：

  1. 比较A和B以获得VMASK：比较A和B的元素，生成一个位掩码VMASK。如果a[i] >= b[i]，则VMASK[i]为1，否则为0。
  2. 将A的掩码存储到C：使用VMASK，把满足条件（a[i] >= b[i]）的元素从A存储到C。
  3. 取反VMASK：取反VMASK，使得之前为0的位变为1，反之亦然。
  4. 将B的掩码存储到C：使用取反后的VMASK，把不满足条件（a[i] < b[i]）的元素从B存储到C。
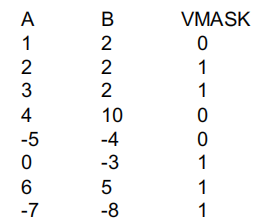
image-20241221190258100

2.11 掩码向量指令（Masked Vector Instructions）

掩码向量指令用于在向量处理器中根据掩码位决定哪些操作结果需要被写回。根据掩码的不同状态，可以优化执行效率和资源使用。

  1. 简单实现 (Simple Implementation)：

  • 方法： 执行所有 N 个操作，根据掩码决定是否写回结果。

  • 示例：

    • 对于每对元素A[i]和B[i]，计算结果C[i]。
    • 如果掩码M[i] = 1，则结果被写入C[i]；如果M[i] = 0，则结果不被写回。

  • 特性： 所有运算都执行，但根据掩码来控制哪些结果被写入存储。

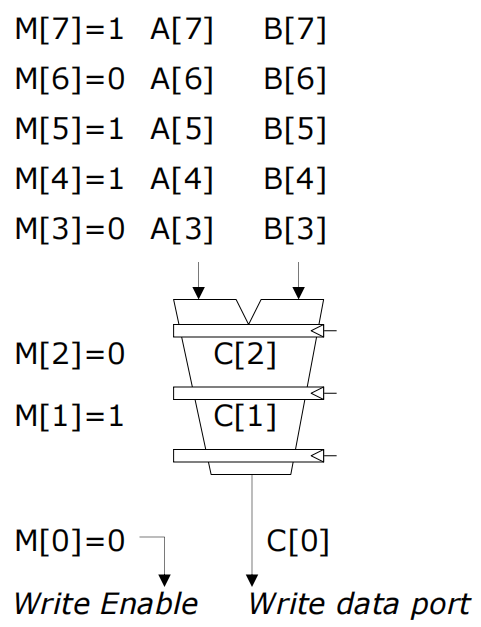
image-20241221191048802
  1. 密度-时间实现 (Density-Time Implementation)：
  • 方法： 扫描掩码向量，仅执行掩码不为零的元素。
  • 示例：
    • 仅对M[i] = 1的元素进行计算和写回。
    • 例如，如果M[7]=1，则仅计算A[7]和B[7]，并将结果写回C[5]。
  • 特性： 通过跳过掩码为零的操作减少计算量，提高效率。
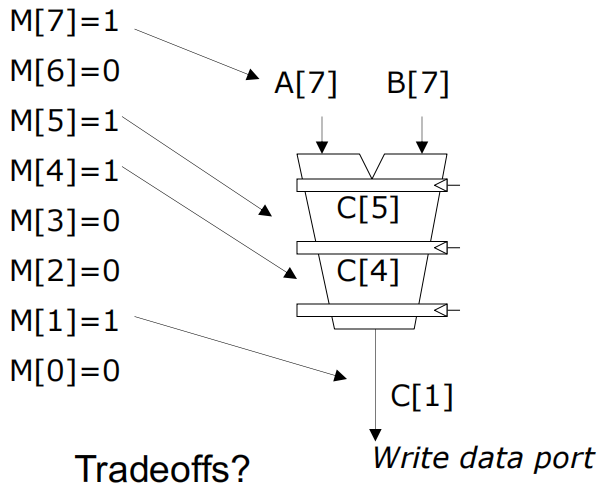
image-20241221191428009
  1. 权衡 (Tradeoffs)：
  • 简单实现的缺点：
    • 即使条件不满足，所有指令仍需执行，浪费计算资源。
    • 某些向量处理器可能在条件执行时仅控制标志寄存器的写操作，可能导致错误。
  • 密度-时间实现的优点和缺点：
    • 优点： 仅对必要的元素进行计算，节省时间和资源。
    • 缺点： 需要额外的逻辑来扫描和选择非零掩码的元素，可能增加复杂性。
  • 有些向量处理器针对带条件的向量执行时，仅控制向目标寄存器的写操作，可能会有除法错误

2.12 Some Issues

  1. 步长与 memory bank 数量：
  • 只要步长和 memory bank 数量互为质数，并且有足够多的 memory bank 来覆盖 memory bank 访问延迟，就可以实现每周期一个元素的吞吐量。
  1. 矩阵的存储格式：
  • 行优先 (Row Major)：在内存中，矩阵中一行的连续元素是连续存储的。
  • 列优先 (Column Major)：在内存中，矩阵中一列的连续元素是连续存储的。
  • 访问不同维度的考虑：当从行访问转为列访问时，步长需要改变。这是因为行和列在内存中的布局不同。

2.13 矩阵乘法中的 memory bank 冲突

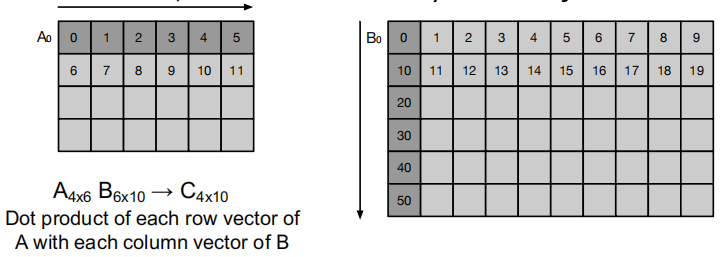
image-20241221193146506

矩阵 A 和 B 都以行优先顺序存储在内存中。

加载A的第0行到向量寄存器V1：

  • 每次访问时，地址增加1以访问下一个列元素。
  • 访问步长为1（即连续存储）。

加载B的第0列到向量寄存器V2：

  • 每次访问时，地址增加10以访问下一个列元素。
  • 访问步长为10（即跳过整行来访问列元素）。

不同步长导致的冲突：

  • 不同的访问步长（例如，A的步长为 1，B的步长为 10）可能导致存储体冲突。
  • 存储体冲突是指在同一时间访问相同存储体的多个请求，导致性能下降。

如何最小化冲突？

2.14 最小化存储体冲突的方法

  1. 增加更多的存储体：
    • 通过增加存储体的数量，可以减少同一时间对同一存储体的访问请求，从而降低冲突的可能性。
  2. 每个存储体增加更多的端口：
    • 为每个存储体增加更多的访问端口，使得同一时间可以处理更多的访问请求，从而缓解冲突。
  3. 更好的数据布局以匹配访问模式：
    • 根据访问模式优化数据在内存中的布局，使得访问请求更均匀地分布在多个存储体上。
    • 问题： 这种方法是否总是可行？在某些情况下，由于数据和访问模式的复杂性，优化布局可能是困难的或不现实的。
  4. 更好的地址到存储体的映射：
    • 通过优化地址如何映射到存储体，可以减少冲突。
    • 例如，随机化映射： 使用随机化的方式将地址映射到存储体，以减少可能的冲突。
    • 参考文献： Rau的研究“Pseudo-randomly interleaved memory”中讨论了这种技术（ISCA 1991）。

2.15 向量指令执行

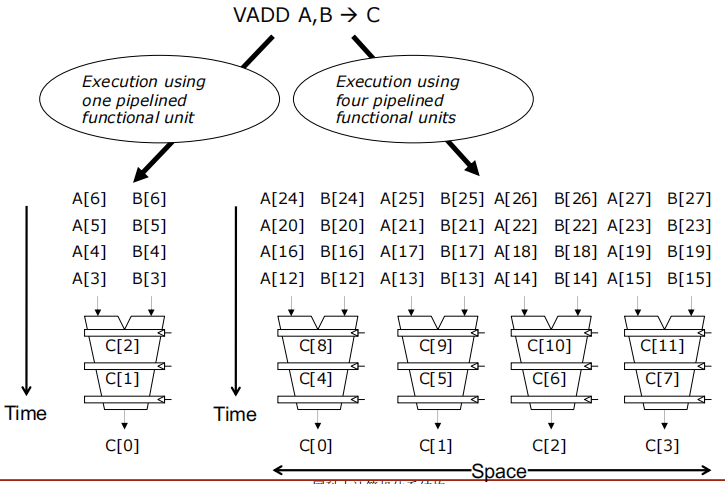
image-20241221194526366

使用一个流水线功能单元（Execution using one pipelined functional unit）：

  • 向量A和B的元素成对地通过单个流水线功能单元进行计算。
  • 由于只有一个功能单元，计算需要依次进行。

使用四个流水线功能单元（Execution using four pipelined functional units）：

  • 向量A和B的元素被分为多个组，每组通过不同的功能单元并行计算。
  • 这种配置允许同时处理多个计算任务，显著提高了处理速度。

2.16 向量单元结构

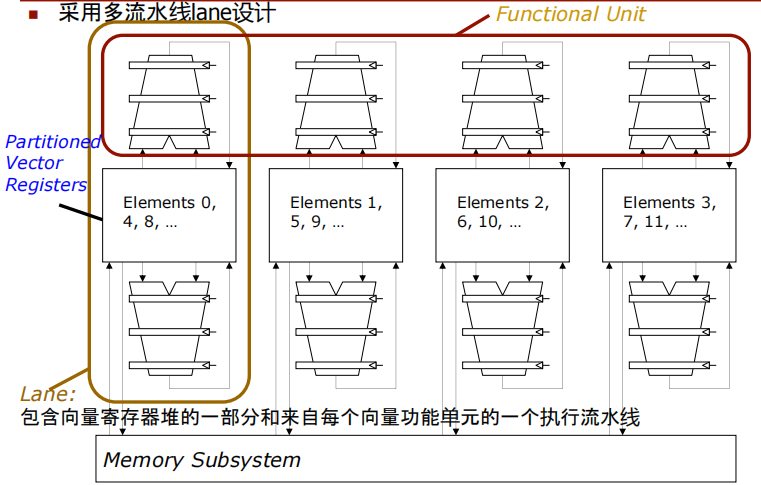
采用多流水线（lane）设计：

  • 每个lane包含一部分向量寄存器堆和一个来自每个向量功能单元的执行流水线。这样可以在同一时间并行处理多个数据元素，提高计算效率。

  • 划分的向量寄存器（Partitioned Vector Registers）：向量寄存器被分割成多个部分，每部分与一个lane相关联，这样可以在多个lane之间分配和管理数据。

  • 元素分配：各个lane处理不同索引的元素，例如，第一个lane处理元素0、4、8等，第二个lane处理元素1、5、9等。

  • 内存子系统（Memory Subsystem）：与多个lane连接，用于提供数据存取支持。

image-20241221195246588

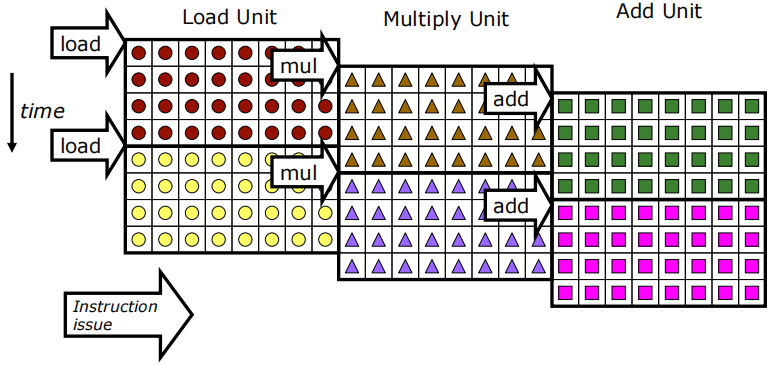
2.17 向量指令级并行性

可以重叠多个向量指令的执行：

  • 通过在不同的阶段同时处理不同的指令，可以实现更高的并行性和效率。

示例机器配置：

  • 每个向量寄存器有32个元素。

  • 共有8条流水线（lanes）。

  • 在稳定状态下，每个周期可以完成24个操作，同时每个周期发出1条向量指令。

image-20241221195642988

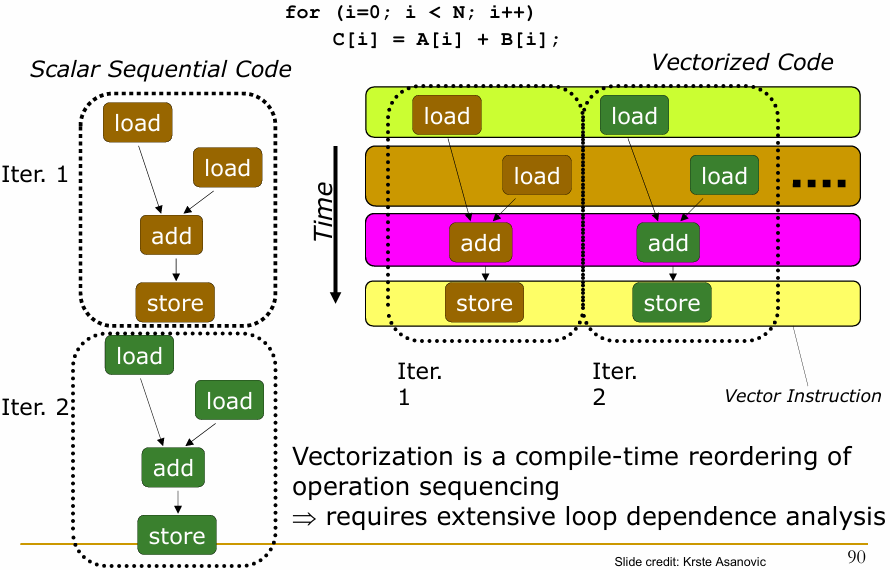
2.18 自动化代码向量化

for (i = 0; i < N; i++)
    C[i] = A[i] + B[i]
  1. 标量代码执行（Iter. 1 和 Iter. 2）：

  • 每次迭代，程序依次执行加载、加法和存储操作。

  • 这种线性执行方式在处理大量数据时可能效率低下，因为每个操作需要等待前一个操作完成。

  1. 向量化代码执行：
  • 向量化方法通过重叠多个操作的执行，将其组合成大的向量指令块。
  • 在时间轴上，多个加载、加法和存储操作可以并行进行，大大提高了处理速度。

向量化是一种在编译时对操作顺序进行重排的过程。

需要对循环依赖进行广泛分析，以确保操作可以安全地并行执行而不破坏数据的正确性。

image-20241221200111660

3. 向量/SIMD处理总结

  1. 向量/SIMD机器的优势：
    • 利用规则数据级并行性：
      • 向量/SIMD机器擅长在具有规则结构的数据上进行并行操作。
      • 同一操作可以同时在多个数据元素上执行。
    • 性能提升和设计简化：
      • 通过消除向量内的依赖关系，向量/SIMD处理不仅提高了性能，还简化了设计。
  2. 性能提升的限制：
    • 代码的向量化能力：
      • 性能提升受到代码可向量化程度的限制。
      • 标量操作会限制向量机器的性能，因为这些操作无法并行处理。
    • Amdahl定律：
      • 提醒我们，即使某部分程序可以高度并行化，程序中不可并行化的部分仍然会限制整体性能提升。
    • CRAY-1的例子：
      • CRAY-1在其时代是最快的标量计算机，这说明即使在向量机器中，标量计算的能力也非常重要。
  3. 现有指令集架构（ISA）中的SIMD操作：
    • 许多现有的指令集架构都包括类似向量的SIMD操作：
      • Intel的MMX/SSEn/AVX系列
      • PowerPC的AltiVec
      • ARM的高级SIMD（Advanced SIMD）
posted @ 2024-12-22 14:03  Astron_fjh  阅读(22)  评论(0)  编辑  收藏  举报