DDCA —— 网络、数据中心与可靠性

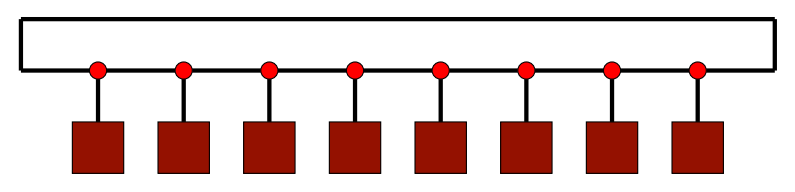
1. Ring

每个节点连接到一个 \(3 \times 3\) switch，该 switch 负责在节点和其两个相邻节点之间传递消息。

实际上，它是一个重复的总线：可以同时传输多条消息。

缺点：二等分带宽为 2，平均需要 \(N/2\) 跳。

2. 拓扑示例

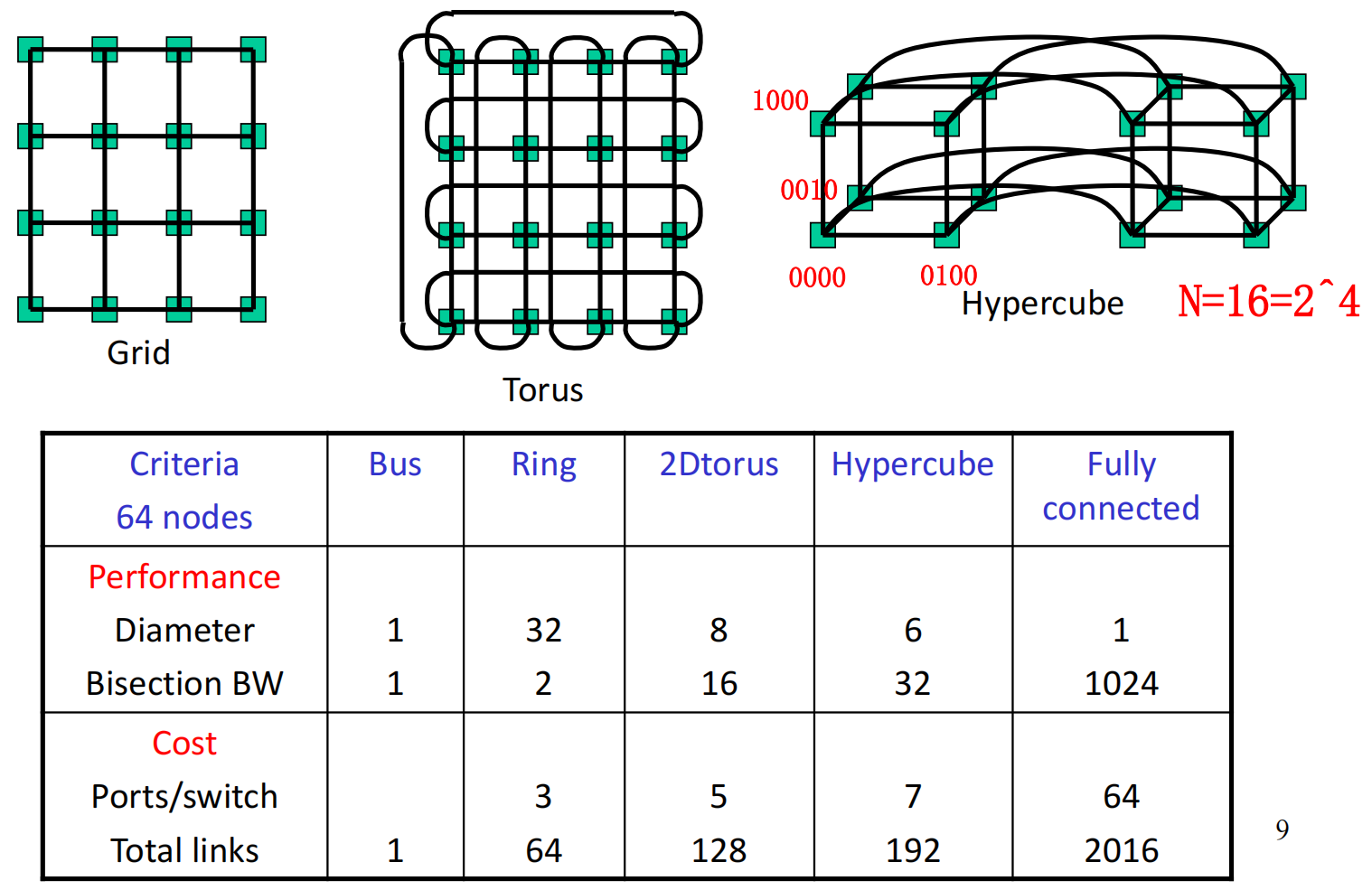
3. k-ary d-Cube

k-ary d-cube 是一个 d 维数组，每个维度包含 k 个元素。数组中两个元素如果在某一维度上的值相差 1（取模 k），则它们之间有一条连接。

节点数量：\(N=k^d\)

当 \(N = 64\)，对于 Torus 为 \(8^2\)，对于 Hypercube 为 \(2^6\)。

所以该 Torus 为一个 2 维网络，该 Hypercube 为一个 6 维网络。

Torus 网络的坐标可以用 (5,6) 表示，Hypercube 网络的坐标可以用 000001 表示。

• switch 数量：\(N\)

• switch 度数：\(2d+1\)

• 链路数量：\(Nd\)

• 每个节点的引脚数：\(2wd\)

• 平均路由距离：\(\frac{d(k-1)}{4}\)

• 直径：\(\frac{d(k-1)}{2}\)

• 二分带宽：\(2wk^{d-1}\)

• switch 复杂度：\((2d+1)^2\)

对于超立方体的调整：

• 超立方体的 switch 度数、链路数量、每个节点的引脚数、二分带宽均为上述值的一半。
• 超立方体的直径和平均路由距离是上述值的两倍。
• 超立方体的交换机复杂度为 \((d+1)^2\)。
• 超立方体与 k-ary d-cube 的主要区别是，它没有左右邻居连接。

维度的取舍：

1. 维度 \(d\) 增大时：！！！k 和 d 是相互制约的关系！！！

• 优点：
  • 平均路由距离 \(\frac{d(k-1)}{4}\) 减小，意味着数据包在网络中传播的跳数减少，从而提升通信效率。
  • 网络直径 \(\frac{d(k-1)}{2}\) 减小，意味着任意两个节点之间的最远距离缩短，通信时延降低。
• 缺点：
  • 每个交换机的度数 \(2d+1\) 增加，意味着每个 switch 需要支持更多的端口，硬件复杂度和成本上升。
  • 链路数量 \(Nd\) 增加，网络的布线复杂度上升。
  • 二分带宽 \(2wk^{d-1}\) 增加，对网络性能是好事，但实现成本也会提升。

3. 互联网络

性能

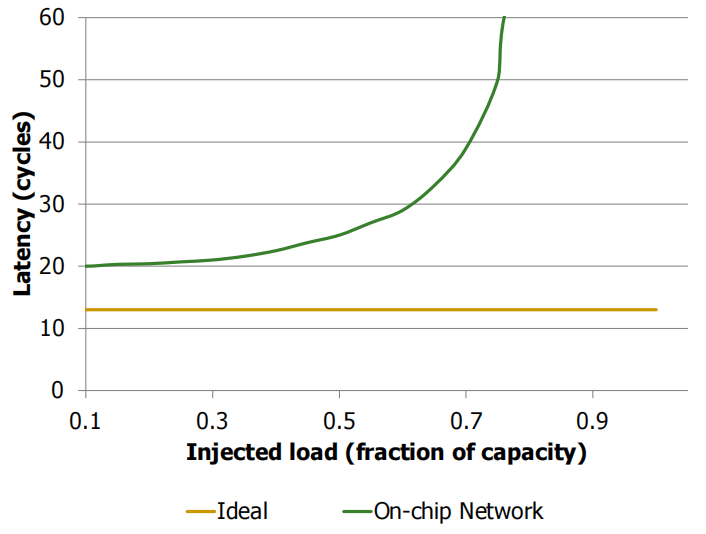
横轴：Injection rate into the network，即网络负载的注入速率，也可理解为数据发送的速率。

纵轴：Latency，即数据在网络中传输所需的时间。

绿色曲线显示了随着负载（Injection Rate）的增加，网络的延迟表现。

• 在低负载下，延迟接近零负载延迟 (Zero Load Latency)。
• 随着负载增加，网络资源变得拥塞，延迟迅速上升。
• 在接近饱和吞吐量 (Saturation Throughput) 时，延迟会急剧增长。

3.1 理想延迟

仅由源节点到目的节点之间的线延迟 (Wire Delay) 决定。

\[T_{ideal} = \frac{D}{v} + \frac{L}{b} \]

• D = 曼哈顿距离 (Manhattan Distance)：

  • 两个点之间的距离，沿着相互垂直的轴测量。

  • 例如：在网格中，从源到目的地只能沿着水平和垂直方向移动，而不能沿对角线直接穿过。

• v = 传播速度 (Propagation Velocity)：信号在网络中传播的速度。

• L = 包大小 (Packet Size)：数据包的总大小。

• b = 信道带宽 (Channel Bandwidth)：信道每单位时间可以传输的数据量。

3.2 真实延迟

专用布线不切实际 (Dedicated wiring impractical)

• 在实际互连网络中，使用长距离专用布线的成本和实现难度较高，因此需要其他方法来优化布线。

• 为了克服长导线的时延问题，将长导线分成多段，每一段之间插入路由器来进行数据中继传输。

\[T_{actual} = \frac{D}{v} + \frac{L}{b} + H \cdot T_{router} + T_c \]

• D = 曼哈顿距离 (Manhattan Distance)

• v = 传播速度 (Propagation Velocity)

• L = 包大小 (Packet Size)

• b = 信道带宽 (Channel Bandwidth)

• H = 跳数 (Hops)：数据包在网络中从源节点到目标节点所经过的路由器数量。

• \(T_{router} =\) 路由器延迟（Router latency）：数据包通过一个路由器所需的时间，包括存储、转发和处理的时间。

• \(T_c =\) 由竞争引起的延迟 (Latency due to contention)：由于网络中多个数据包同时争用同一信道或资源而导致的延迟。

3.3 负载延迟曲线

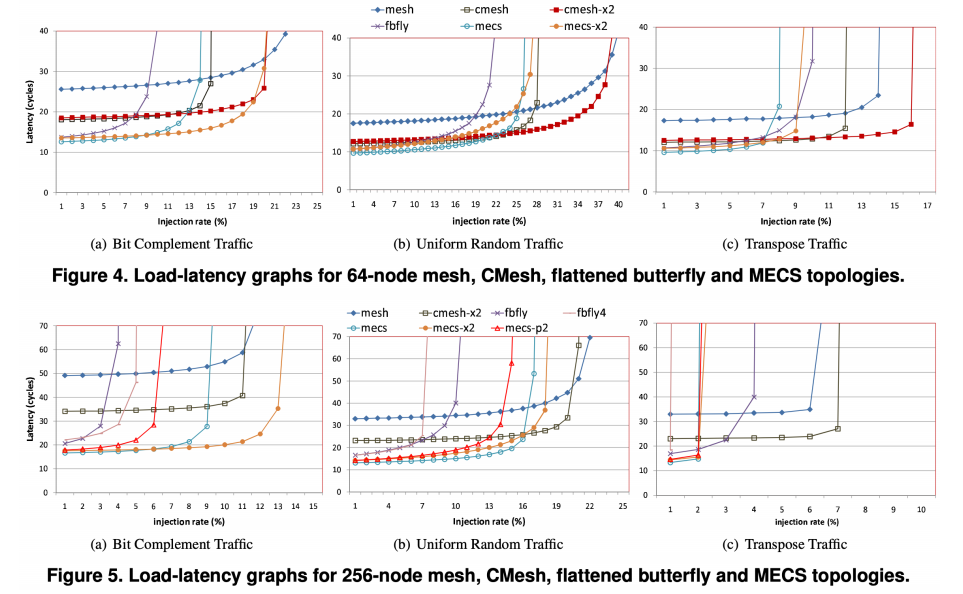
3.4 网络性能指标

数据包延迟 (Packet latency, 平均/最大)

• 平均延迟：数据包从源点到目的地的平均传输时间。
• 最大延迟：所有数据包中最长的传输时间。

往返延迟 (Round trip latency, 平均/最大)

• 请求-响应层面：指从发送请求到接收响应所需的时间。
• 缓存未命中服务时间 (Cache miss service time)：当缓存未命中时，数据被获取并返回所花费的时间。

饱和吞吐量 (Saturation throughput)

• 网络在达到饱和状态时，仍然能够维持的最大数据传输速率。

应用级性能 (Application-level performance)

• 执行时间 (Execution time)：应用程序完成其任务所需的时间。

系统性能 (System performance)

• 作业吞吐量 (Job throughput)：系统在单位时间内能够完成的任务数量。
• 受到线程/应用之间干扰的影响 (Affected by interference among threads/applications)：不同线程或应用之间的资源争用会影响整体系统性能。

4. On-Chip Networks

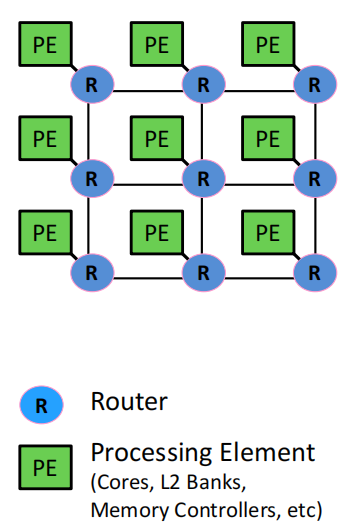
连接核心、缓存、内存控制器等：主要目标是将处理核心、缓存和内存控制器等模块连接起来。

总线和交叉开关不具备可扩展性：传统的总线（Bus）和交叉开关（Crossbar）结构在规模增大时会遇到性能瓶颈，不适用于大规模片上网络。

通常采用分组交换（Packet Switched）：数据在网络中通过分组的方式进行传输，而不是传统的电路交换。

二维网格（2D Mesh）：常用的拓扑结构：2D网格是片上网络中最常用的拓扑结构，简单且易于实现。

XY路由与FIFO或轮询端口仲裁常见：

• XY路由：数据先沿X轴移动，再沿Y轴移动到达目标节点。
• FIFO（先进先出）或轮询仲裁（Round Robin Port Arbitration）常用于端口资源分配。

虚拟信道缓冲常见：使用虚拟信道（Virtual Channel）来缓冲数据，有助于缓解拥塞并提高网络效率。

主要用于缓存未命中和内存请求：片上网络的主要任务是服务于缓存未命中（Cache Misses）和内存请求（Memory Requests），以加速数据传输。

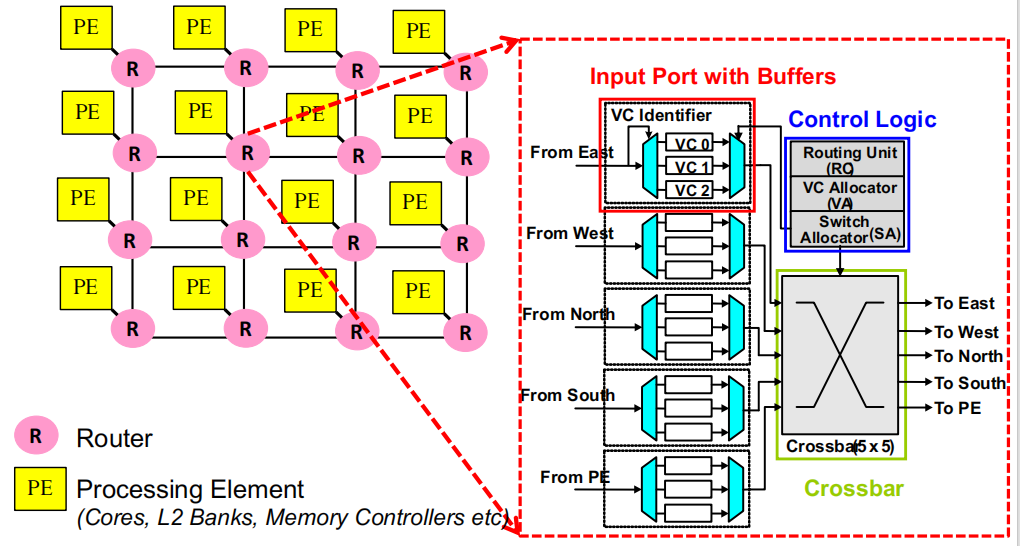
4.1 On-Chip vs. Off-Chip Interconnects（片上互连与片外互连的比较）

1. 片上互连的优势

• 核心之间的低延迟
• 没有引脚限制
• 丰富且低功耗的布线资源
• 带宽非常高
• 全局协调更简单

2. 片上互连的约束/劣势

• 2D基底限制了易于实现的拓扑结构*

• 能量/功耗是关键问题

  • 复杂算法不可取

  • 大型缓冲器不可取

• 逻辑面积和金属层限制了布线资源的使用

3. 成本对比

• 片外互连：主要成本来自通道、引脚、连接器和电缆等。

• 片上互连：主要成本是存储和交换结构（布线资源丰富）。

4. 设计趋势

• 结果：设计出带宽非常宽但缓冲较少的网络。

5. 通道特性

• 片上互连：传输距离短，延迟低。

6. 工作负载

• 片外互连：大型并行应用程序中的多芯片通信流量。
• 片上互连：多核架构下的缓存/内存通信流量。