高等数字集成电路课程作业（二）
高等数字集成电路课程作业的记录，都是很简单的toy design，包括秒表、超前进位加法器、Booth乘法器+Wallance加法树和桶形移位器。
1. 跑表
1.1 设计功能与要求
设计一个跑表时序逻辑电路，通过按钮控制及数字显示，有时分秒显示，可以清零、开始和暂停。系统主时钟频率为 \(10MHz\)。
其中按钮Clear实现清零功能（任意状态按下时分秒值清零并停止计时）、按钮Start/Stop实现开始和暂停功能（若当前状态为停止则按下继续进行计时，若当前状态为计时则按下暂停计时）。
数字显示为XX : XX : XX形式，时分秒各为2位数字。对每位数字使用4位二进制编码输出表示（hr_h[3:0]，hr_l[3:0]，min_h[3:0]，min_l[3:0] ，sec_h[3:0]，sec_l[3:0]）。
顶层模块名为stop_watch，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| Clk | I | 1 | 系统时钟，10MHz |
| rst_n | I | 1 | 异步复位，低电平有效 |
| Clear | I | 1 | 清零按钮，上升沿有效 |
| start_stop | I | 1 | 开始/暂停按钮，上升沿有效 |
| hr_h | O | 4 | 时高位输出，取值0~9 |
| hr_l | O | 4 | 时低位输出，取值0~9 |
| min_h | O | 4 | 分高位输出，取值0~9 |
| min_l | O | 4 | 分低位输出，取值0~9 |
| sec_h | O | 4 | 秒高位输出，取值0~9 |
| sec_l | O | 4 | 秒低位输出，取值0~9 |
设计要求：
Verilog实现代码可综合，给出综合以及仿真结果（说明：为加快仿真速度，代码用于仿真时可以缩短秒计数周期，如每100个时钟周期更新一次秒计数值，正常情况下每10000000个时钟周期才更新一次秒计数值）。
1.2 RTL实现架构
该设计的顶层模块为stop_watch：
module stop_watch(
input wire Clk,
input wire rst_n,
input wire Clear,
input wire start_stop,
output wire [3:0] hr_h,
output wire [3:0] hr_l,
output wire [3:0] min_h,
output wire [3:0] min_l,
output wire [3:0] sec_h,
output wire [3:0] sec_l
);
检测Clear和start_stop的上升沿：
reg Clear_d;
reg start_stop_d;
wire Clear_pos;
wire start_stop_pos;
assign Clear_pos = (!Clear_d && Clear) ? 1 : 0;
assign start_stop_pos = (!start_stop_d && start_stop) ? 1 : 0;
// detect posedge
always @(posedge Clk or negedge rst_n) begin
if (!rst_n) begin
Clear_d <= 1'b0;
start_stop_d <= 1'b0;
end else begin
Clear_d <= Clear;
start_stop_d <= start_stop;
end
end
使用一个 1bit 寄存器start_reg决定是否计时：
reg start_reg;
always @(posedge Clk or negedge rst_n) begin
if (!rst_n)
start_reg <= 1'b0;
else begin
if (Clear_pos)
start_reg <= 1'b0;
else if (start_stop_pos) begin
if (start_reg)
start_reg <= 1'b0;
else
start_reg <= 1'b1;
end else
start_reg <= start_reg;
end
end
计时逻辑：
reg [6:0] cnt;
reg [5:0] cnt_sec;
reg [5:0] cnt_min;
reg [4:0] cnt_hr;
wire cnt_full;
wire cnt_sec_full;
wire cnt_min_full;
wire cnt_hr_full;
assign cnt_full = (cnt == 7'd99) ? 1 : 0;
assign cnt_sec_full = ((cnt_sec == 6'd59) && cnt_full) ? 1 : 0;
assign cnt_min_full = ((cnt_min == 6'd59) && cnt_sec_full) ? 1 : 0;
assign cnt_hr_full = ((cnt_hr == 5'd23) && cnt_min_full) ? 1 : 0;
always @(posedge Clk or negedge rst_n) begin
if (!rst_n) begin
cnt <= 7'd0;
cnt_sec <= 6'd0;
cnt_min <= 6'd0;
cnt_hr <= 6'd0;
end else if (Clear_pos) begin
cnt <= 7'd0;
cnt_sec <= 6'd0;
cnt_min <= 6'd0;
cnt_hr <= 6'd0;
end else if (start_reg == 1'b1) begin
if (cnt_full == 1'b1) begin
cnt <= 7'd0;
cnt_sec <= cnt_sec + 1'b1;
end else begin
cnt <= cnt + 1'b1;
cnt_sec <= cnt_sec;
end
if (cnt_sec_full == 1'b1) begin
cnt_sec <= 6'd0;
cnt_min <= cnt_min + 1'b1;
end else
cnt_min <= cnt_min;
if (cnt_min_full == 1'b1) begin
cnt_min <= 6'd0;
cnt_hr <= cnt_hr + 1'b1;
end else
cnt_hr <= cnt_hr;
if (cnt_hr_full == 1'b1)
cnt_hr <= 5'd0;
end
end
还有一个子模块bin2bcd将cnt_sec，cnt_min和cnt_hr转换成 bcd 格式：
bin2bcd u_hr_bin2bcd(
.bin_in ({3'b000, cnt_hr}),
.bcd_out ({hr_h, hr_l})
);
bin2bcd u_min_bin2bcd(
.bin_in ({2'b00, cnt_min}),
.bcd_out ({min_h, min_l})
);
bin2bcd u_sec_bin2bcd(
.bin_in ({2'b00, cnt_min}),
.bcd_out ({sec_h, sec_l})
);
1.3 RTL仿真结果
1.3.1 测试用例说明
先start_stop有效开始计时，计时到一半Clear有效清零，再让start_stop有效开始计时，过一段时间后再让start_stop有效停止计时。
initial begin
rst_n = 1'b0;
Clk = 1'b0;
Clear = 1'b0;
start_stop = 1'b0;
#50;
rst_n = 1'b1;
#(50 * `period);
start_stop = 1'b1;
#(50 * `period);
start_stop = 1'b0;
#(50000 * `period);
Clear = 1'b1;
#(50 * `period)
Clear = 1'b0;
#(5000 * `period)
start_stop = 1'b1;
#(50 * `period);
start_stop = 1'b0;
#(500000 * `period);
start_stop = 1'b1;
#(50 * `period);
start_stop = 1'b0;
#(5000 * `period);
$finish;
end
1.3.2 测试结果波形
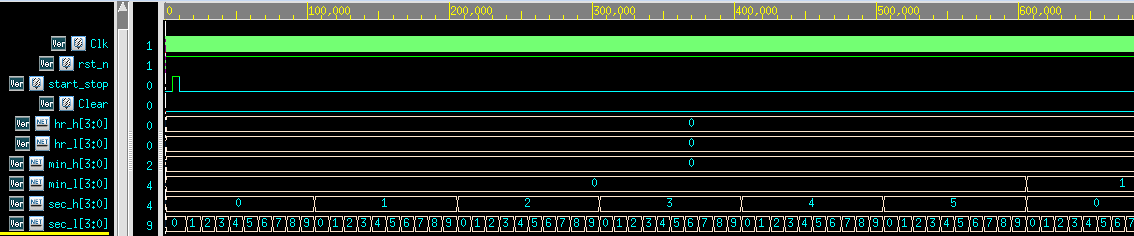
- 第一个红框中，
Clear有效，停止计时并计时清零，随后start_stop有效，开始计时。 - 第二个红框中，
start_stop有效，停止计时。
结论：该输出正确，证明设计正确。
1.4 ASIC综合结果
使用 Design Compiler 进行综合，使用 smic180 工艺，tcl中部分约束如下：
# 使用 slow 工艺角
set target_library " slow.db "
set link_library "* $target_library "
set symbol_library " smic18.sdb "
# 时钟约束
create_clock -period 100 -waveform {0 50} [get_ports Clk] -name Clk
set_clock_latency 1 Clk
set_clock_transition 2 Clk
set_clock_uncertainty 10 -setup Clk
set_clock_uncertainty 3 -hold Clk
set_drive 0 [list Clk rst_n]
# 输入驱动使用 NAND2x1
set_driving_cell -lib_cell NAND2X1 [get_ports {Clear start_stop}]
# 输入输出延迟设为 20ns
set_input_delay 20 -clock [get_clocks Clk] [get_ports {Clear start_stop}]
set_output_delay 20 [get_ports {hr_h hr_l min_h min_l sec_h sec_l}]
# 综合后的面积越小越好
set_max_area 0
1.4.1 关键路径延时 & 最大运行频率
DC综合后的 timing report 如上所示，
-
data arrival time为26.17 ns，是满足时序要求的时钟周期时间，也是关键路径延时。 -
最大运行频率计算公式如下所示，
-
因此最大运行频率为 \(f_{max} = \frac{1}{26.17 \times 10^{-9}} \approx 38.2MHz\) （时钟约束周期为100ns）
-
由于时序裕量（Slack）为
64.7 ns，说明设计目前满足时序要求，并且时钟周期可以进一步优化以提高频率。
1.4.2 ASIC面积
-
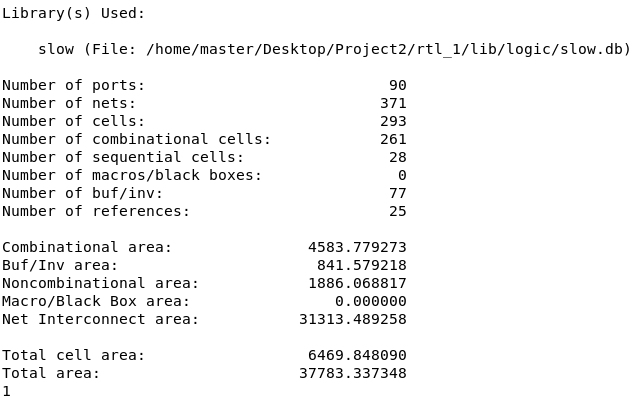
由于 DC 综合并没有真实走线，主要看总的
cell area，可以看到Total cell area为 \(6469.848090\mu m^2\)； -
Number of cells: 总的逻辑单元数，包括组合逻辑单元和时序单元，共 293 个；
-
Number of combinational cells: 组合逻辑单元数量，共 261 个；
-
Number of sequential cells: 时序逻辑单元数量，共 28 个，这些单元包含触发器或寄存器。
1.4.3 综合后的Schematic
2. 快速加法器
2.1 设计功能与要求
实现快速加法器组合逻辑，要实现的功能如下：
输入为两个32位有符号补码数，输出33位相加结果。要求采用超前进位（Carry-look-ahead）结构。
顶层模块名为add_tc_16_16，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| A | I | 32 | 输入数据，二进制补码 |
| B | I | 32 | 输入数据，二进制补码 |
| Sum | O | 33 | 输出和 \(a+b\)，二进制补码 |
设计要求：
Verilog实现代码可综合，逻辑延迟越小越好，给出综合以及仿真结果（参考ASIC综合结果：SMIC 55nm工艺下工作时钟频率大于500 MHz）。
2.2 算法原理与算法设计
对于更宽的加法器 \(N\)，行波进位加法器关键路径越长，限制了加法器的性能，对于高速处理器等将是个极大的瓶颈。所以，本文介绍的超前进位加法器优化改进行波进位器的关键路径。RCA的缺点在于第 \(k\) 位的进位 \(C_k\) 必须依赖于前一级的 \(C_{k-1}\)，所以最高位的进位将必须等待之前所有级进位计算完毕后才能计算出结果。所以，超前进位加法器的思想是并行计算进位 \(C_k\)。
观察上式 \(s\) 和 \(c\)，将共有部分分别定义：
对于 \(N\) 比特 CLA 加法器，进位与和公式将重新写为如下：
其中：
以 \(4\) 比特 CLA 加法器为例，其进位链与和公式分别计算如下：
根据上述式子，可以计算出 \(C_i\) 和 \(S_i\)，其结构图为：
2.3 RTL实现架构
原先是纯组合逻辑设计，为了查看关键路径延时及最大运行频率，在输入和输出添加了寄存器：
module add_tc_16_16(
input wire clk,
input wire rst_n,
input wire [31:0] A,
input wire [31:0] B,
output reg [32:0] Sum_reg
);
assign overflow = (A_reg[31] == B_reg[31]) && (S[31] != A_reg[31]); // 判断是否溢出
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin
A_reg <= 32'd0;
B_reg <= 32'd0;
Sum_reg <= 33'd0;
end else begin
A_reg <= A;
B_reg <= B;
if (overflow) // 若溢出
Sum_reg <= {C[32], S}; // 用进位作符号位
else
Sum_reg <= {S[31], S};
end
end
生成信号、传播信号、进位信号和求和信号的计算：
wire [31:0] G; // 生成信号
wire [31:0] P; // 传播信号
wire [32:0] C; // 进位信号
wire [31:0] S; // 求和信号
assign G = A_reg & B_reg;
assign P = A_reg ^ B_reg;
assign C[0] = 0;
genvar i;
generate
for (i = 1; i <= 32; i = i+1) begin
assign C[i] = G[i-1] | (P[i-1] & C[i-1]);
end
endgenerate
generate
for (i = 0; i < 32; i = i+1) begin
assign S[i] = P[i] ^ C[i];
end
endgenerate
2.4 RTL 仿真结果
2.4.1 测试用例说明
使用了5个测试用例：
- 测试 1: 正数加正数，\(A=12345\)，\(B=67890\)；
- 测试 2: 负数加负数，\(A=−12345\)，\(B=−67890\)；
- 测试 3: 正数加负数，\(A=12345\)，\(B=−67890\)；
- 测试 4: 溢出情况 (最大正数加 1)，\(A=2^{31}−1=2147483647\)，\(B=1\)；
- 测试 5: 最小负数加 -1，\(A=−2^{31}=−2147483648\)，\(B=-1\)。
2.4.2 测试结果波形
结论：可以看到所有计算都正确，说明该设计正确。
2.5 ASIC综合结果
使用 Design Compiler 进行综合，使用 smic180 工艺，tcl中部分约束如下：
# clk
create_clock -period 10 -waveform {0 5} [get_ports clk] -name clk
set_clock_latency 0.1 clk
set_clock_transition 0.2 clk
set_clock_uncertainty 1 -setup clk
set_clock_uncertainty 0.3 -hold clk
set_drive 0 [list clk rst_n]
set_driving_cell -lib_cell NAND2X1 [get_ports {A B}]
set_input_delay 2 -clock [get_clocks clk] {A B}
set_output_delay 2 [get_ports Sum_reg]
set_load 2 [all_outputs]
# 综合后的面积越小越好
set_max_area 0
2.5.1 关键路径延时 & 最大运行频率
DC综合后的 timing report 如上所示，
-
data arrival time为8.74 ns，是满足时序要求的时钟周期时间，也是关键路径延时。 -
最大运行频率计算公式如下所示，
- 因此最大运行频率为 \(f_{max} = \frac{1}{8.74 \times 10^{-9}} \approx 114.44MHz\) （时钟约束周期为10ns）
- 由于时序裕量（Slack）为
0.01 ns，说明设计目前满足时序要求。
2.5.2 ASIC面积
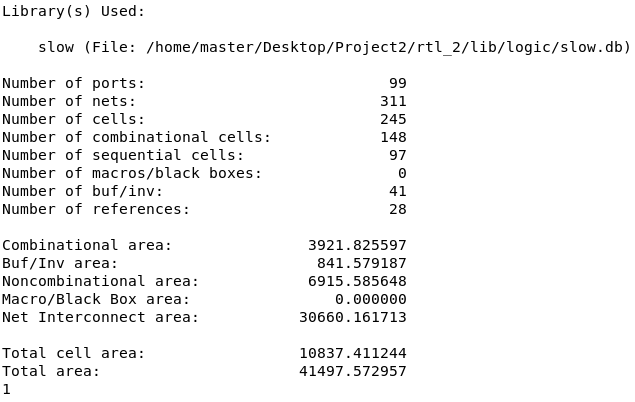
- 由于 DC 综合并没有真实走线，主要看总的
cell area，可以看到Total cell area为 \(10837.411244\mu m^2\)； - Number of cells: 总的逻辑单元数，包括组合逻辑单元和时序单元，共 245 个；
- Number of combinational cells: 组合逻辑单元数量，共 148 个；
- Number of sequential cells: 时序逻辑单元数量，共 97 个，这些单元包含触发器或寄存器。
2.5.3 综合后的Schematic
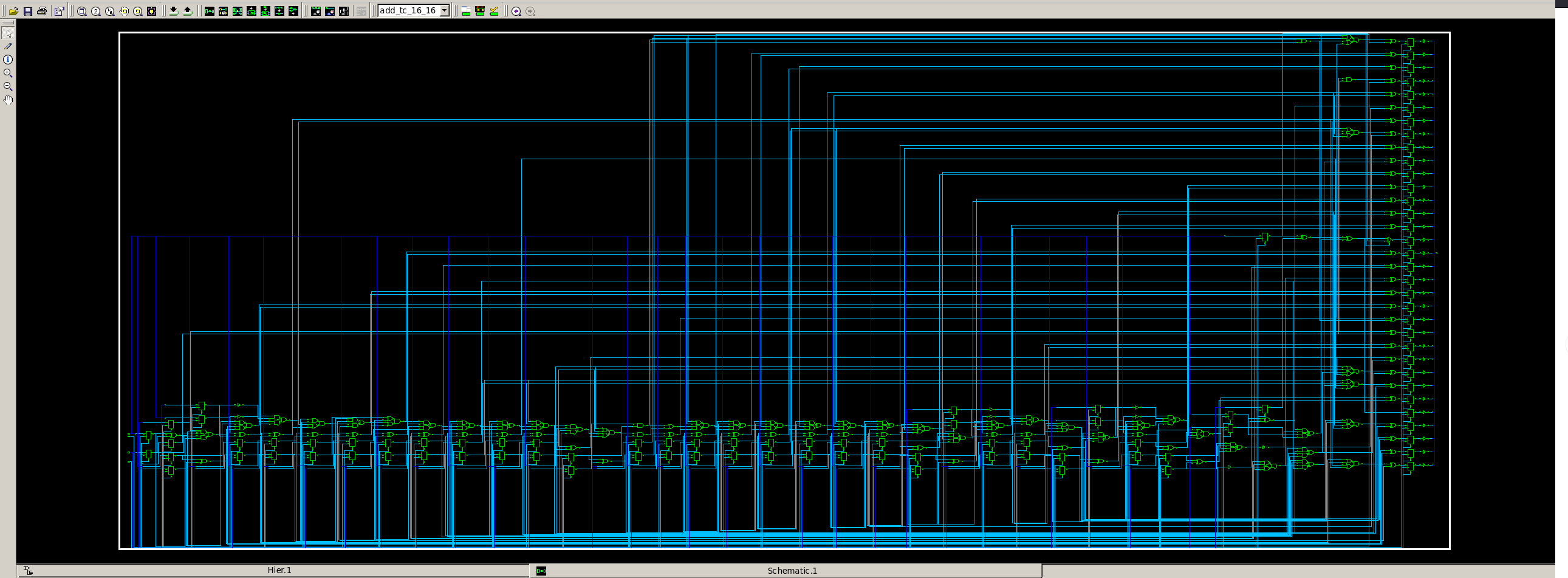
3. 快速乘法器
3.1 设计功能与要求
实现快速乘法器组合逻辑，要实现的功能如下：
输入为两个16位有符号数，输出32位相乘结果。要求采用Booth编码和Wallace树型结构。
计算例子：
0110000010000000\(\times\)1000000000000001=11001111110000000110000010000000
\((24704) \times (-32767) = (-809475968)\)
顶层模块名为mul_tc_16_16，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| a | I | 16 | 输入数据，二进制补码 |
| b | I | 16 | 输入数据，二进制补码 |
| product | O | 32 | 输出乘积 a*b，二进制补码 |
设计要求：
Verilog实现代码可综合，逻辑延迟越小越好，给出综合以及仿真结果（参考ASIC综合结果：SMIC 55nm工艺下工作时钟频率大于500 MHz）。
3.2 算法原理与算法设计
3.2.1 二进制乘法转换成booth乘法运算
假设有一个8位乘数（Multiplier）：0011_1110，它将产生5行非零的部分积。如果把该数字记成另一种形式：0100_00(-1)0（可以验证是同一个数字）。
\(0011\_1110 = 0 \times 2^7 + 0 \times 2^6 + 1 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 62\)
\(0100\_00(-1)0 = 0 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 0 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + (-1) \times 2^1 + 0 \times 2^0 = 62\)
所以，\(0011\_1110 = 0100\_00(-1)0 = 2^6 - 2^1 = 0100\_0000 - 0000\_0010\)。
计算\(0010\_0001 \times 0011\_1110\)，在这里可以首先将乘数\(0011\_1110\)改写为\(0100\_0000-0000\_0010\)，即根据乘法分配律得：
此时，对于乘数，我们从需要计算5次的部分积，变成了计算2次部分积。
3.2.2 Radix-2 Booth乘法器
Radix-2 Booth乘法器，即是基2 Booth乘法器，基为2的一次方。
数的表示方法：\(B=-B_{n-1}2^{n-1} + \left(\sum^{n-2}_{i=0}B_i \cdot 2^i\right)\)，其中\(B_i\)是该二进制数中第\(i\)位的值，它可以是 0 或 1。
将\(N\)为比特数\(B\)展开，在\(N\)位比特数\(B\)的最后一位\(B_0\)后添加一个辅助位\(B_{-1}\)，且\(B_{-1}=0\)。
从上式中得出，其基系数为：\(Coef_i=(B_{i-1}-B_i)\)
将A与B相乘，则：
对于\(B\)的第\(n\)位和第\(n-1\)位，从上式可以发现，\(B\)可以通过相邻的比特位的减法和2的\(n\)次方相乘而得。如果\(A\)、\(B\)两数相乘，从\(B\)的\(-1\)和\(0\)位逐次向高位检查，累计\(A \times B\)的结果。
以下是Radix-2 Booth编码表，根据两个数据位的编码进行加法、减法还是仅仅移位操作。
| \(B_n\) | \(B_{n+1}\) | 操作 |
|---|---|---|
| 0 | 0 | \(+0\) |
| 0 | 1 | \(+[A]_{补}\) |
| 1 | 0 | \(+[-A]_{补}\) |
| 1 | 1 | \(+0\) |
3.2.3 Radix-4 Booth乘法器
基于上面的推理，上式的\(B\)还可以写作下式（位宽为偶数）：
从上式中得出，其基系数为：\(Coef_i=(-2B_{i+1}+B_i+B_{i-1})\)
将A与B相乘，则：
以下是Radix-4 Booth编码表，根据两个数据位的编码进行加法、减法还是仅仅移位操作。
| \(B_{i+1}\) | \(B_i\) | \(B_{i-1}\) | \(-2B_{i+1}+B_i+B_{i-1}\) | 部分积操作 |
|---|---|---|---|---|
| 0 | 0 | 0 | +0 | 0 |
| 0 | 0 | 1 | +1 | \(1 \times A\) |
| 0 | 1 | 0 | +1 | \(1 \times A\) |
| 0 | 1 | 1 | +2 | \(2 \times A\) |
| 1 | 0 | 0 | -2 | \(-2 \times A\) |
| 1 | 0 | 1 | -1 | \(-1 \times A\) |
| 1 | 1 | 0 | -1 | \(-1 \times A\) |
| 1 | 1 | 1 | -0 | 0 |
以下为6比特数9的Radix-2 Booth和Radix-4 Booth编码例子：
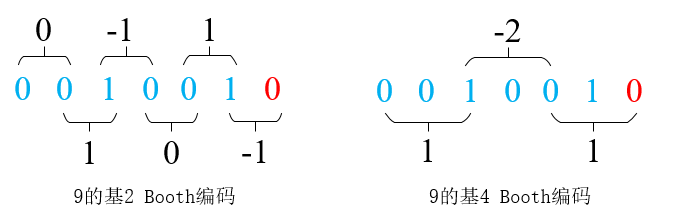
从基2看9：\(9 = 0 \times 2^4 + 1 \times 2^4 + (-1) \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + (-1) \times 2^0\)
从基4看9：\(9 = 1 \times 4^2 + (-2) \times 4^1 + 1 \times 4^0\)
其阵列表示如下：
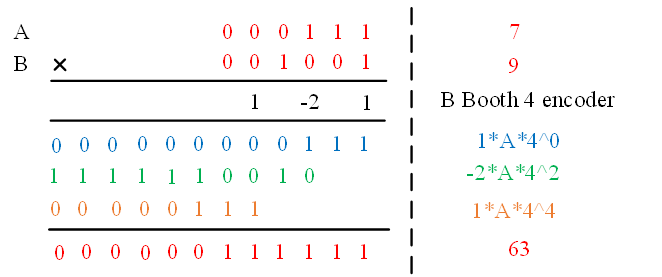
可以看出，6比特乘数的Radix-2 Booth算法部分累积和个数为6，而Radix-4的部分累积和数为3。
相比于Radix-2 Booth编码，Radix-4 Booth编码将使得乘法累积的部分和数减少一半，其基系数只涉及到移位和补码计算。
对于二进制码为\(1010\dots1010\)的乘数（1与0交替），如果采用Radix-2 Booth编码，则部分和累积的输入有几乎一半为被乘数的补码，所以，相比于普通的阵列乘法器，Radix-2 Booth编码的乘法器性能不升反降，Radix-4 Booth编码可以避免以上问题。
3.2.4 Wallace Tree原理
传统的全加器因为有3个输入（\(A, B,C_{in}\)），产生2个输出（\(S,C_{out}\)），故常把全加器也称为3-2压缩器。
即\(n\)个全加器每次可以把\(m\)个\(n\)位的数相加转换成\(2m/3\)个数相加，因此，\(n\)个全加器每次可以把\(m\)个\(n\)位的数相加转换成\(2m/3\)个数相加，再用一层全加器转换成\(4m/9\)个数相加，直到转换成2个数，再用加法器把最后两个数相加。
Wallace Tree便是基于3-2压缩器构成的，主要优化思路是使用尽量少的加法单元对部分积的累加进行压缩。
在一个乘法阵列中，把一个同一列中的部分积（位）与右边一列传来的进位通过进位保存加法器（CSA）或者其他位数压缩电路尽可能早地相加，所产生的Carryout送向左边一列，所产生的“和”位继续在本列传播，这就构成了Wallace Tree乘法器。
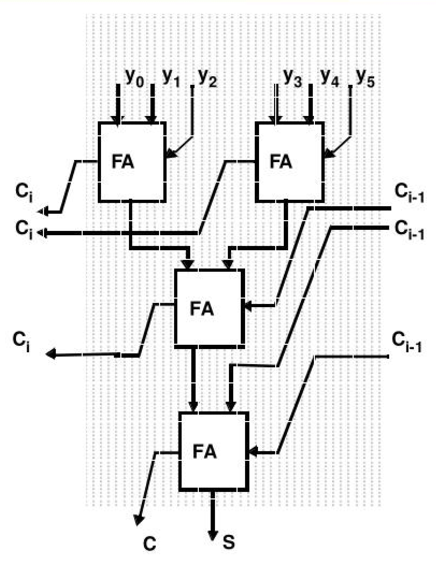
下面展示了在分析8个1位的数使用Wallace Tree压缩的实现（6个全加器和1个半加器），其对应的就是程序中mul_tc_16_16模块的实现逻辑。
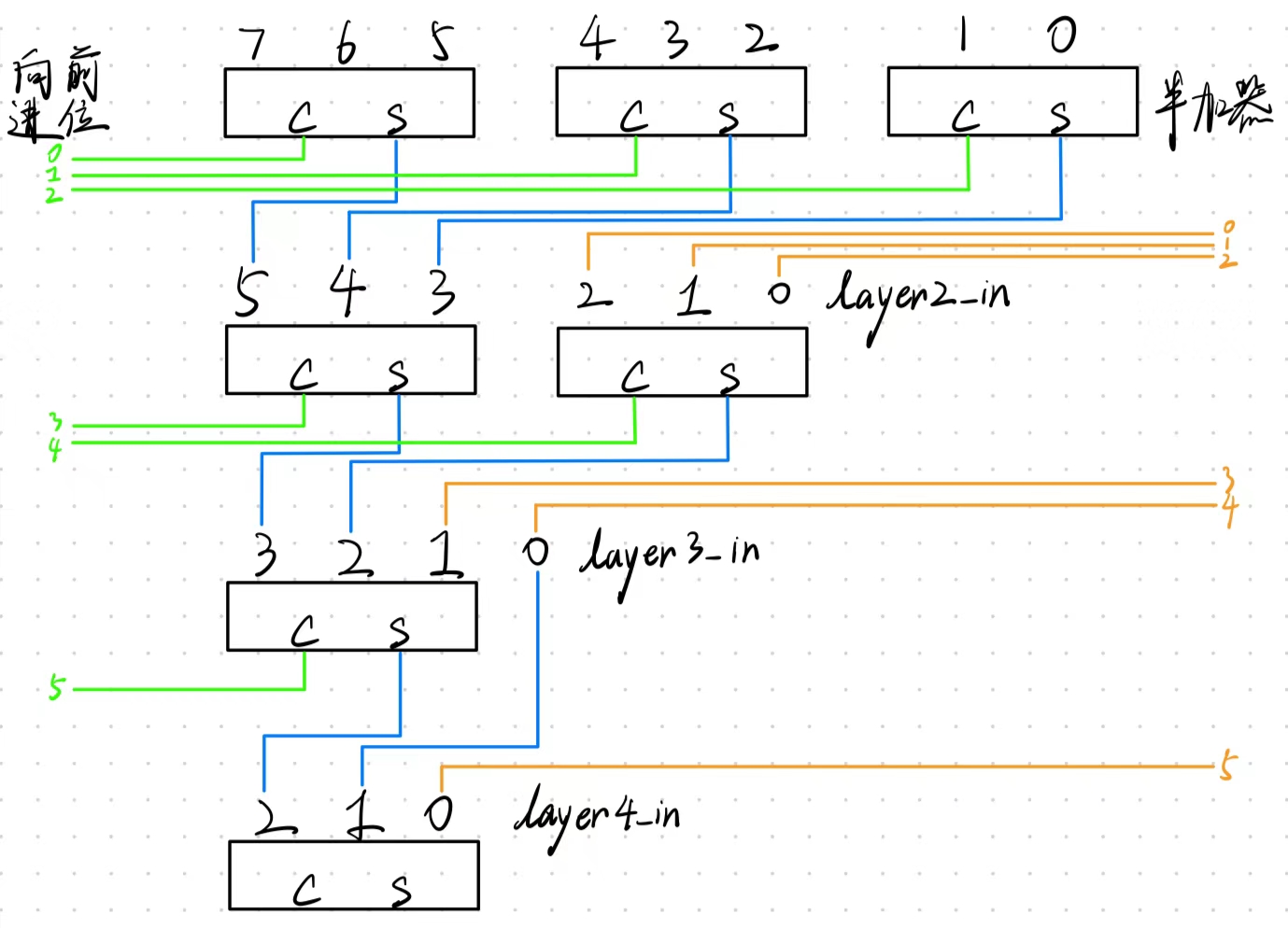
3.3 RTL实现架构
原先是纯组合逻辑设计，为了查看关键路径延时及最大运行频率，在输入和输出添加了寄存器。
u_booth_encoder 模块先计算a和b相乘的部分积，再将部分积传输到 u_wallace_tree_32_8 中进行求和，输出计算出的和 C 和以及进位 S，再传输到超前进位加法器 u_add_tc_32_32 进行求和算出最终结果：
module mul_tc_16_16(
input wire clk,
input wire rst_n,
input wire [15:0] a,
input wire [15:0] b,
output reg [31:0] product_reg
);
reg [15:0] a_reg;
reg [15:0] b_reg;
wire [31:0] partial[7:0];
wire [31:0] C; // 32位数的 wallace 树最上面的输出进位C
wire [31:0] S; // 32位数的 wallace 树最上面的输出和S
wire [5:0] Cout;//
wire [32:0] Sum;
wire [31:0] product;
assign product = Sum[31:0];
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin
a_reg <= 16'd0;
b_reg <= 16'd0;
product_reg <= 32'd0;
end else begin
a_reg <= a;
b_reg <= b;
product_reg <= product;
end
end
booth_encoder u_booth_encoder(
.A (a_reg),
.B (b_reg),
.partial_product0 (partial[0]),
.partial_product1 (partial[1]),
.partial_product2 (partial[2]),
.partial_product3 (partial[3]),
.partial_product4 (partial[4]),
.partial_product5 (partial[5]),
.partial_product6 (partial[6]),
.partial_product7 (partial[7])
);
wallace_tree_32_8 u_wallace_tree_32_8(
.in0 (partial[0]),
.in1 (partial[1]),
.in2 (partial[2]),
.in3 (partial[3]),
.in4 (partial[4]),
.in5 (partial[5]),
.in6 (partial[6]),
.in7 (partial[7]),
.C (C),
.S (S),
.Cout (Cout)
);
add_tc_32_32 u_add_tc_32_32(
.A (S),
.B ({C[30:0], 1'b0}),
.Sum (Sum)
);
endmodule
booth_encoder 模块中的核心代码为：
envar i;
generate
for (i = 0; i < 8; i = i + 1) begin : booth_gen
assign partial_product[i] =
(B_ext[2*i+2 : 2*i] == 3'b000) ? 32'd0 :
(B_ext[2*i+2 : 2*i] == 3'b001) ? A_ext << (2*i) :
(B_ext[2*i+2 : 2*i] == 3'b010) ? A_ext << (2*i) :
(B_ext[2*i+2 : 2*i] == 3'b011) ? A_ext << (2*i + 1) :
(B_ext[2*i+2 : 2*i] == 3'b100) ? -(A_ext << (2*i + 1)) :
(B_ext[2*i+2 : 2*i] == 3'b101) ? -(A_ext << (2*i)) :
(B_ext[2*i+2 : 2*i] == 3'b110) ? -(A_ext << (2*i)) :
32'd0;
end
endgenerate
wallace_tree_32_8 模块由多个 wallace_tree_8_1 模块组成：
module wallace_tree_32_8(
input wire [31:0] in0,
input wire [31:0] in1,
input wire [31:0] in2,
input wire [31:0] in3,
input wire [31:0] in4,
input wire [31:0] in5,
input wire [31:0] in6,
input wire [31:0] in7,
output wire [31:0] C, // 32位数的 wallace 树最上面的输出进位C
output wire [31:0] S, // 32位数的 wallace 树最上面的输出和S
output wire [5:0] Cout // 32位数的 wallace 树最左侧的 Cout
);
wire [5:0] Cout_wire[32:0];
assign Cout_wire[0] = 6'b00_0000; // 最右列没有进位输入
genvar i;
generate
for (i = 0; i <= 31; i = i+1) begin
wallace_tree_8_1 u_wallace_8_1(
.A ({in7[i], in6[i], in5[i], in4[i], in3[i], in2[i], in1[i], in0[i]}),
.Cin (Cout_wire[i]),
.Cout (Cout_wire[i+1]),
.C (C[i]),
.S (S[i])
);
end
endgenerate
assign Cout = Cout_wire[32];
endmodule
wallace_tree_8_1 模块为 8 个 1-bit 数求和，由6个全加器和1个半加器组成：
module wallace_tree_8_1(
input wire [7:0] A,
input wire [5:0] Cin, // 右侧列的Cout
output wire [5:0] Cout, // 左侧列的Cin
output wire C, // 最后一级输出的Cout
output wire S // 最后一级输出的S
);
// layer 1
wire [5:0] layer2_in;
assign layer2_in[2:0] = Cin[2:0];
full_adder u_fa_l1_1(
.A (A[5]),
.B (A[6]),
.Cin (A[7]),
.Cout (Cout[0]),
.S (layer2_in[5])
);
full_adder u_fa_l1_2(
.A (A[2]),
.B (A[3]),
.Cin (A[4]),
.Cout (Cout[1]),
.S (layer2_in[4])
);
half_adder u_ha_l1_3(
.A (A[0]),
.B (A[1]),
.Cout (Cout[2]),
.S (layer2_in[3])
);
// layer 2
wire [3:0] layer3_in;
assign layer3_in[1:0] = Cin[4:3];
full_adder u_fa_l2_1(
.A (layer2_in[3]),
.B (layer2_in[4]),
.Cin (layer2_in[5]),
.Cout (Cout[3]),
.S (layer3_in[3])
);
full_adder u_fa_l2_2(
.A (layer2_in[0]),
.B (layer2_in[1]),
.Cin (layer2_in[2]),
.Cout (Cout[4]),
.S (layer3_in[2])
);
// layer 3
wire [2:0] layer4_in;
assign layer4_in[1:0] = {layer3_in[0], Cin[5]};
full_adder u_fa_l3_1(
.A (layer3_in[1]),
.B (layer3_in[2]),
.Cin (layer3_in[3]),
.Cout (Cout[5]),
.S (layer4_in[2])
);
// layer 4
full_adder u_fa_l4_1(
.A (layer4_in[0]),
.B (layer4_in[1]),
.Cin (layer4_in[2]),
.Cout (C),
.S (S)
);
endmodule
3.4 RTL仿真结果
3.4.1 测试用例说明
使用随机测试用例，并对特殊情况\(16'hFFFF\)和\(16'hFFFF\)进行测试：
initial begin
a = 16'd7;
b = 16'd9;
#(5*`period);
a = 16'hffff;
b = 16'hffff;
#(5*`period);
repeat(3)
begin
a = {$random} % 17'b10000;
b = {$random} % 17'b10000;
#(5*`period);
end
$finish;
end
3.4.2 测试结果波形
- \(a=7, b=9, product = 63\)；
- \(a = -1,b = -1,product = 1\)；
- \(a=4, b=1, product=4\)；
- \(a=9,b=3,product=27\)；
- \(a=13,b=13,product=169\)。
结论：以上测试用例都通过，设计正确。
3.5 ASIC综合结果
使用 Design Compiler 进行综合，使用 smic180 工艺，tcl中部分约束如下：
# clk
create_clock -period 10 -waveform {0 5} [get_ports clk] -name clk
set_clock_latency 0.1 clk
set_clock_transition 0.2 clk
set_clock_uncertainty 1 -setup clk
set_clock_uncertainty 0.3 -hold clk
set_drive 0 [list clk rst_n]
set_driving_cell -lib_cell NAND2X1 [get_ports {a b}]
set_input_delay 2 -clock [get_clocks clk] [get_ports {a b}]
set_output_delay 2 [get_ports product_reg]
set_load 2 [all_outputs]
# 综合后的面积越小越好
set_max_area 0
3.5.1 关键路径延时 & 最大运行频率
DC综合后的 timing report 如上所示，
-
data arrival time为8.86 ns，是满足时序要求的时钟周期时间，也是关键路径延时。 -
最大运行频率计算公式如下所示，
- 因此最大运行频率为 \(f_{max} = \frac{1}{8.86 \times 10^{-9}} \approx 112.9MHz\) （时钟约束周期为10ns）
- 由于时序裕量（Slack）为
0.0 ns，说明设计目前满足时序要求。
3.5.2 ASIC面积
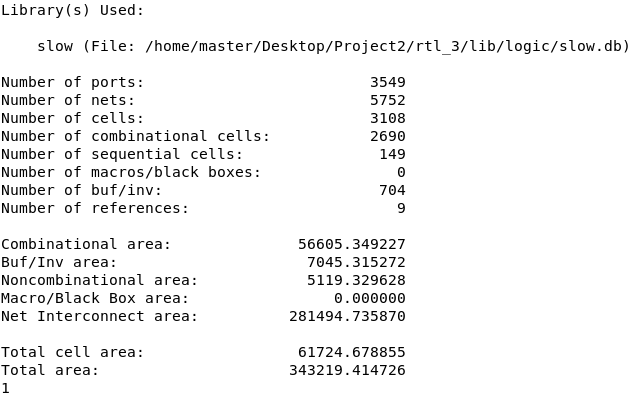
- 由于 DC 综合并没有真实走线，主要看总的
cell area，可以看到Total cell area为 \(61724.678855\mu m^2\)； - Number of cells: 总的逻辑单元数，包括组合逻辑单元和时序单元，共 3108 个；
- Number of combinational cells: 组合逻辑单元数量，共 2690 个；
- Number of sequential cells: 时序逻辑单元数量，共 149 个，这些单元包含触发器或寄存器。
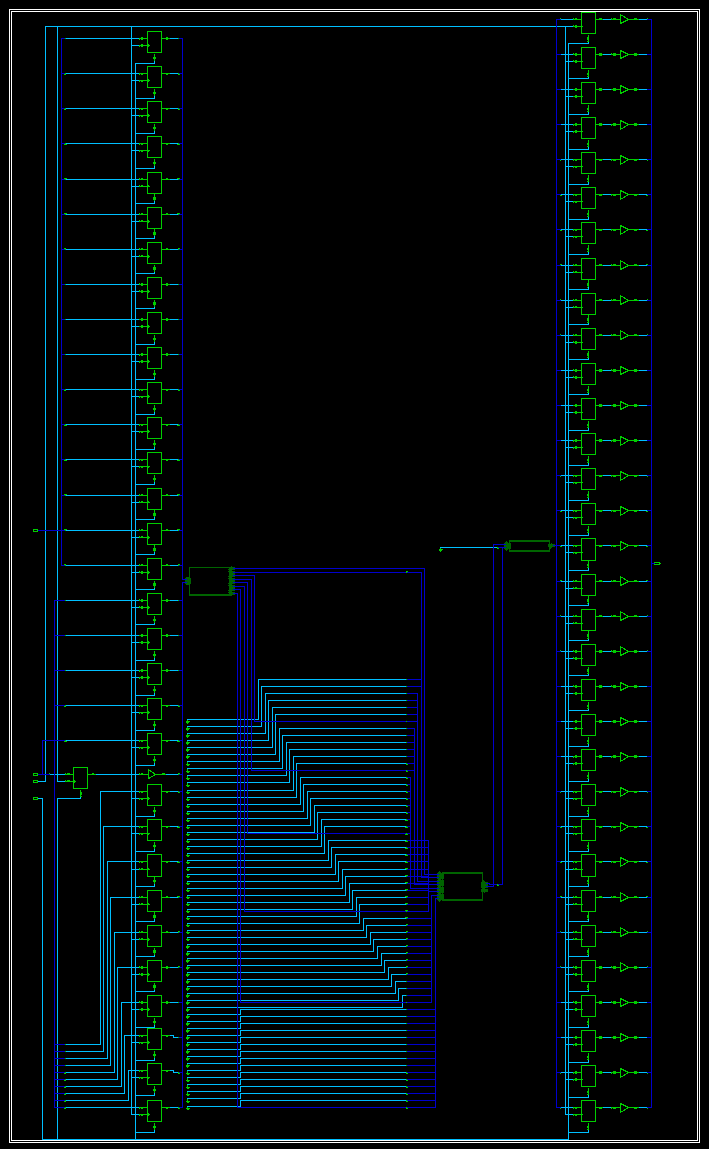
3.5.3 综合后的Schematic
4. 桶形移位器
4.1 设计功能与要求
实现桶形移位器组合逻辑，要实现的功能如下：
输入为32位二进制向量，根据方向和位移值输出循环移位后的32位结果。例如：
输入向量00011000101000000000000000000000，方向左，位移值10，输出向量10000000000000000000000001100010；
输入向量00000000111111110000000000000011，方向右，位移植20，输出向量11110000000000000011000000001111.
顶层模块名为bsh_32，输入输出功能定义：
| 名称 | 方向 | 位宽 | 描述 |
|---|---|---|---|
| data_in | I | 32 | 输入数据 |
| dir | I | 1 | 位移方向：0：循环左移；1：循环右移 |
| sh | I | 5 | 位移值，取值0~31 |
| data_out | O | 32 | 输出数据 |
设计要求：
Verilog实现代码可综合，逻辑延迟越小越好，给出综合以及仿真结果。
4.2 算法原理与算法设计
判断dir的位移方向：
- 若
dir == 0，data_in向左算数位移sh次，data_in向右算数位移32-sh次，两个结果进行或操作； - 若
dir == 1，data_in向右算数位移sh次，data_in向左算数位移32-sh次，两个结果进行或操作。
4.3 RTL实现架构
原先是纯组合逻辑设计，为了查看关键路径延时及最大运行频率，在输入和输出添加了寄存器。
module bsh_32 (
input wire clk,
input wire rst_n,
input wire [31:0] data_in,
input wire dir,
input wire [4:0] sh,
output reg [31:0] data_out_reg
);
reg [31:0] data_in_reg;
reg dir_reg;
reg [4:0] sh_reg;
wire [31:0] data_out;
assign data_out = dir_reg ? ((data_in_reg >> sh_reg) | (data_in_reg << (32-sh_reg))) :
((data_in_reg << sh_reg) | (data_in_reg >> (32-sh_reg)));
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin
data_in_reg <= 32'd0;
dir_reg <= 1'b0;
sh_reg <= 5'd0;
data_out_reg<= 32'd0;
end else begin
data_in_reg <= data_in;
dir_reg <= dir;
sh_reg <= sh;
data_out_reg<= data_out;
end
end
endmodule
4.4 RTL仿真结果
4.4.1 测试用例说明
使用了2个测试用例：
dir = 0，sh = 10，data_in = 32'b0001_1000_1010_0000_0000_0000_0000_0000；dir = 1，sh = 5'd20，data_in = 32'b0000_0000_1111_1111_0000_0000_0000_0011；
4.4.2 测试结果波形
- 第1个测试用例的结果为
data_out = 1000_0000_0000_0000_0000_0000_0110_0010； - 第2个测试用例的结果为
data_out = 1111_0000_0000_0000_0011_0000_0000_1111。
结论：2个测试用例的输出结果正确，说明设计正确。
4.5 ASIC综合结果
使用 Design Compiler 进行综合，使用 smic180 工艺，tcl中部分约束如下：
# clk
create_clock -period 10 -waveform {0 5} [get_ports clk] -name clk
set_clock_latency 0.1 clk
set_clock_transition 0.2 clk
set_clock_uncertainty 1 -setup clk
set_clock_uncertainty 0.3 -hold clk
set_drive 0 [list clk rst_n]
set_driving_cell -lib_cell NAND2X1 [get_ports {data_in dir sh}]
set_input_delay 2 -clock [get_clocks clk] [get_ports {data_in dir sh}]
set_output_delay 2 [get_ports data_out_reg]
set_load 2 [all_outputs]
# 综合后的面积越小越好
set_max_area 0
4.5.1 关键路径延时 & 最大运行频率
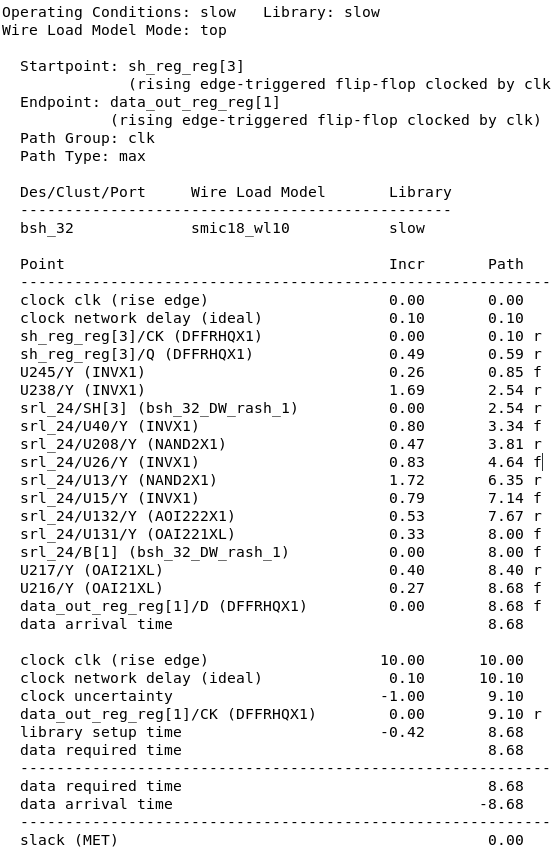
DC综合后的 timing report 如上所示，
-
data arrival time为8.68 ns，是满足时序要求的时钟周期时间，也是关键路径延时。 -
最大运行频率计算公式如下所示，
- 因此最大运行频率为 \(f_{max} = \frac{1}{8.68 \times 10^{-9}} \approx 115.2MHz\) （时钟约束周期为10ns）
- 由于时序裕量（Slack）为
0.0 ns，说明设计目前满足时序要求。
4.5.2 ASIC面积
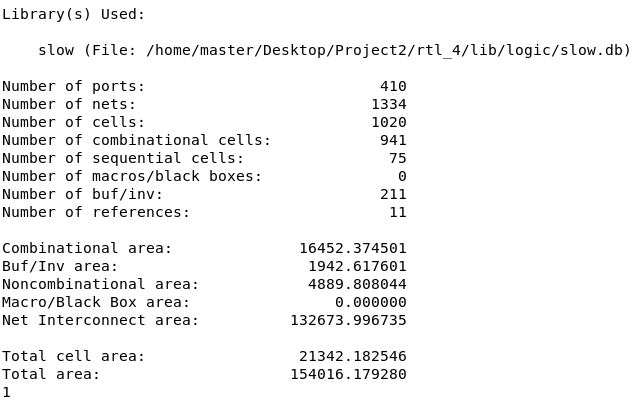
- 由于 DC 综合并没有真实走线，主要看总的
cell area，可以看到Total cell area为 \(21342.182546\mu m^2\)； - Number of cells: 总的逻辑单元数，包括组合逻辑单元和时序单元，共 1020个；
- Number of combinational cells: 组合逻辑单元数量，共 941 个；
- Number of sequential cells: 时序逻辑单元数量，共 75 个，这些单元包含触发器或寄存器。
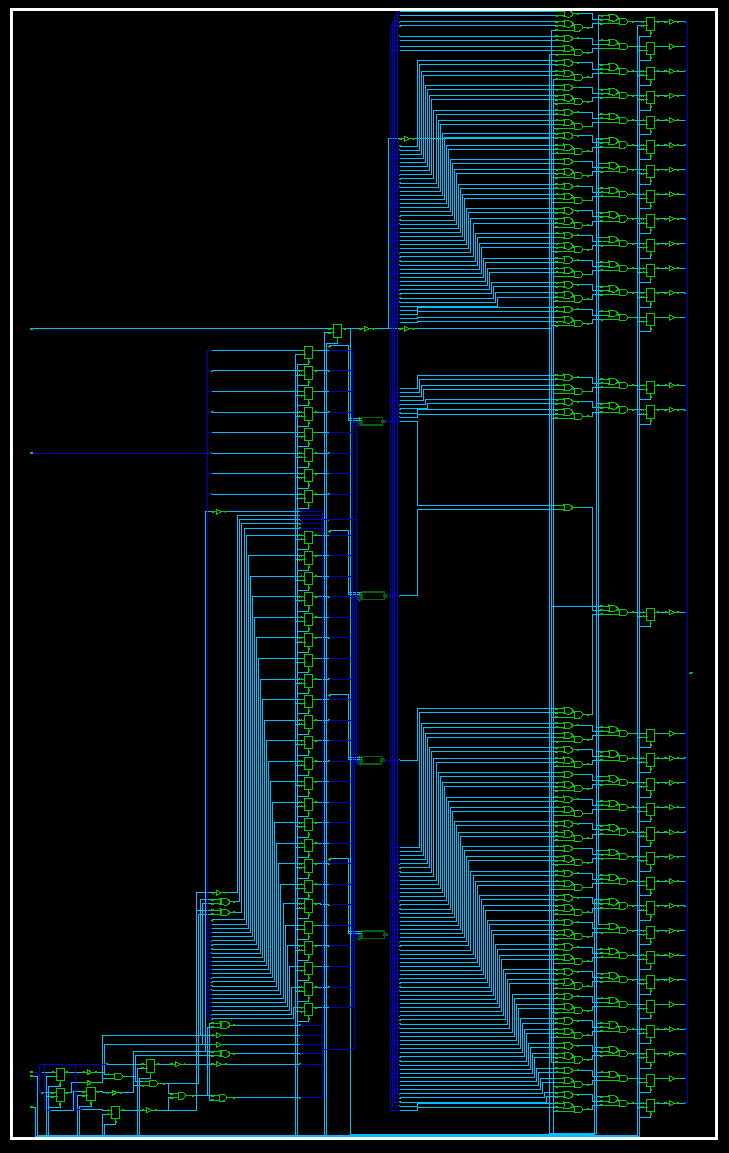
4.5.3 综合后的Schematic
