CUDA编程学习 (4)——thread执行效率
1. Warp 和 SIMD 硬件
1.1 作为调度单位的 Warp

每个 block 分为 32-thread warp
-
在 CUDA 编程模型中,虽然 warp 不是显式编程的一部分,但在硬件实现上,每个 block 会被自动划分成若干个包含 32 个线程的 warp。
-
warp 作为 SM 中的调度单元:SM(Streaming Multiprocessor)会以 warp 为单位进行调度和管理,这意味着在执行时,每次会选择一个 warp 中的 thread 来运行。
-
warp 中的线程以 SIMD 方式执行:SIMD(Single Instruction Multiple Data)是一种并行计算方式,表示一个 warp 中的所有 thread 会同时执行相同的指令,但可以处理不同的数据。
-
thread 数量未来可能变化:当前的 warp 包含 32 个 thread,但在未来的硬件架构中,warp 中的 thread 数量可能会有所改变。
1.2 多维 thread block 中的 warp
首先将 thread block 按行主次线性化为 1D
- 首先是 x 维,其次是 y 维,最后是 z 维,
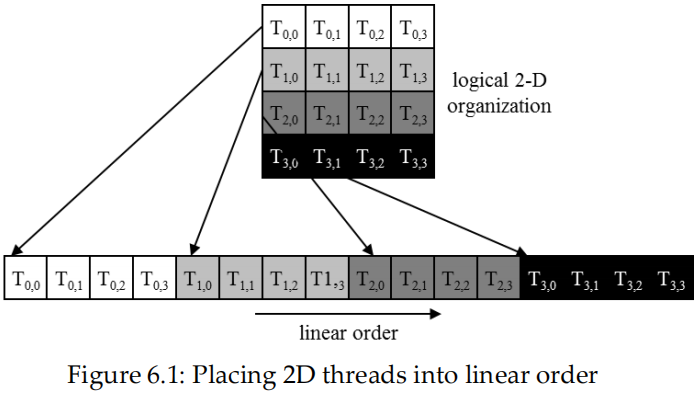
1.3 Block 在线性化后被分区
线性化 block 的划分:
- thread 索引在 warp 中是连续且递增的
- warp 0 从 thread 0 开始
分区方案在不同 device 上是一致的:
- 在不同的 CUDA device 上,warp 的分区方式是相同的,因此可以在控制流中利用这一点进行编程。
- 但是,warp 的确切大小可能会随代际变化:虽然当前 warp 通常包含 32 个 thread,但未来的硬件可能会改变这个大小。
不要依赖 warp 内或 warp 之间的执行顺序:
- CUDA 程序不能依赖 warp 内部或不同 warp 之间的执行顺序,因为 thread 的执行顺序并没有严格的保证。
- 如果 thread 之间存在依赖性,需要使用
__syncthreads()进行同步:当某些 thread 的结果会影响其他 thread 时,必须显式使用同步函数__syncthreads(),否则可能会得到错误的结果。
1.4 SMs 是 SIMD(单指令多数据流)处理器
指令获取、解码和控制的控制单元在多个处理单元之间共享
- 控制开销被最小化(模块1)
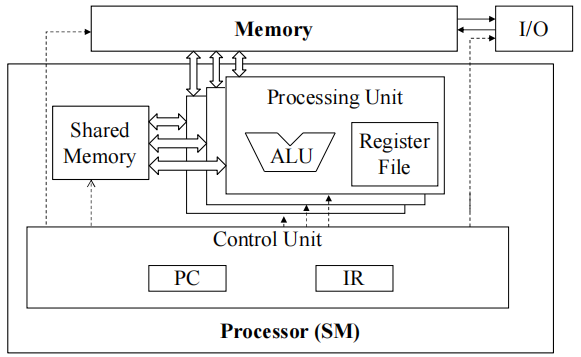
1.5 warp thread 间的 SIMD 执行
warp 中的所有 thread 在任何时间点都必须执行相同的指令
如果所有 thread 都遵循相同的控制流路径,这种方法就能高效运行
- 所有 if-then-else 语句都做出相同的决定
- 所有循环的遍历次数相同
1.6 控制分歧
当同一个 warp 中的 thread 由于做出不同的控制决策而走上不同的控制流路径时,就会发生控制分歧。
- 比如在一个
if语句中,一些 thread 选择走then路径,而另一些线程选择走else路径。 - 或者一些 thread 执行循环的次数比其他 thread 多。
当前 GPU 中,warp 中的 thread 如果选择了不同的控制路径,选择不同路径的 thread 会被串行化执行。
- GPU会依次执行每个控制路径,在执行某个路径时,所有选择该路径的线程会并行执行,而没有选择该路径的线程则会暂停(即这些线程不参与当前路径的执行)。
- 当涉及嵌套控制流语句(如嵌套的
if-else或循环)时,控制分歧的复杂性会增加,不同路径的数量也会变得非常大,进一步增加了执行的开销。
1.6.1 控制分歧示例
当分支或循环条件依赖于 thread 索引时,可能会产生分歧。
具有分歧的示例 kernel 语句:
if (threadIdx.x > 2) {}- 这为一个 block 中的 thread 创建了两条不同的控制路径
- 决策粒度 < warp的大小;thread 0、1 和 2 与第一个 warp 中的其余 thread 遵循不同的路径
没有分歧的示例:
-
if (blockIdx.x > 2) {} -
决策粒度 = block 的大小的倍数;在任何一个 warp 中的所有 thread 都会遵循相同的路径
1.7 示例:向量加法 kernel
// Device Code
// Compute vector sum C = A + B
// Each thread performs one pair-wise addition
__global__
void vecAddKernel(float* A, float* B, float* C, int n)
{
int i = threadIdx.x + blockDim.x * blockIdx.x;
if(i < n) C[i] = A[i] + B[i];
}
1.7.1 对 1000 个元素的向量大小进行分析
-
假设 block 大小为 256 个 thread
- 每个 block 有 8 个 warp
-
block 0、1 和 2 中的所有 thread 都在有效范围内
-
i值从 0 到 767 -
这三个 block 中的 24 个 warp 都不会有控制分歧
-
-
block 3 中的大多数 warp 不会有控制分歧
- warp 0-6 中的 thread 都在有效范围内,因此没有控制分歧
-
block 3 中的一个 warp 会有控制分歧
-
thread 的
i值从 992 到 999 都在有效范围内 -
thread 的
i值从 1000 到 1023 将超出有效范围
-
-
控制分歧导致的串行化效果很小
-
32 个 warp 中只有 1 个有控制分歧
-
对性能的影响可能小于 3%
-
2. 控制分歧对性能的影响
2.1 控制分歧对性能的影响
- 边界条件检查对并行代码的完整功能和稳健性至关重要
- tiled 矩阵乘法 kernel 有许多边界条件检查
- 令人担忧的是,这些检查可能会导致性能严重下降
例如,请看下面的 tile 加载代码:
if(Row < WIDTH && p * TILE_WIDTH + tx < WIDTH) {
ds_M[ty][tx] = M[Row * WIDTH + p * TILE_WIDTH + tx];
} else {
ds_M[ty][tx] = 0.0;
}
if(p * TILE_WIDTH + ty < WIDTH && Col < WIDTH) {
ds_N[ty][tx] = N[(p * TILE_WIDTH + ty) * WIDTH + Col];
} else {
ds_N[ty][tx] = 0.0;
}
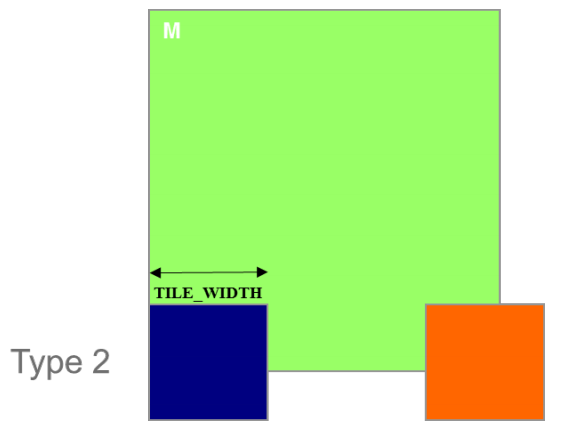
2.2 装载 M tiles 的两种 blocks
- Type 1:直到最后阶段,所有 tile 都在有效区域的 block
- Type 2:部分 tile 一直在有效范围之外的 block
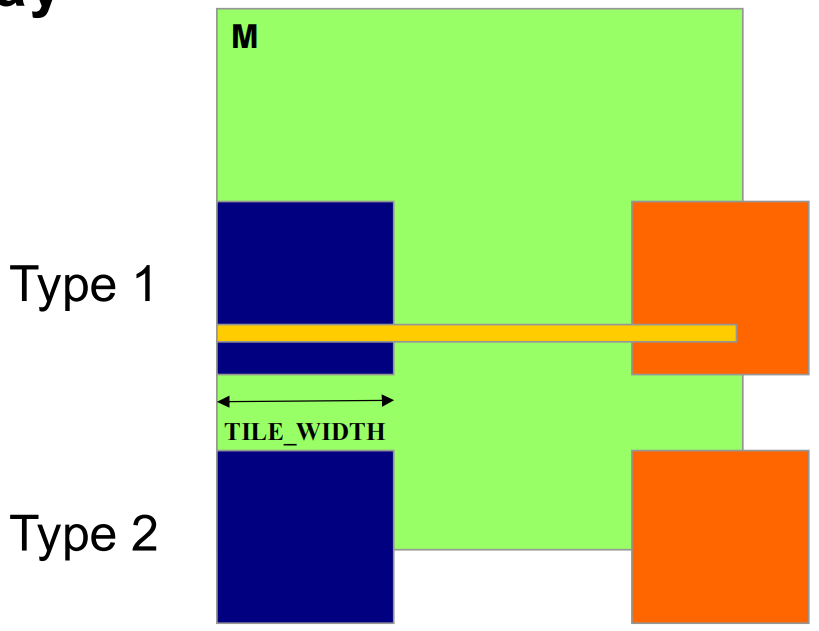
2.3 控制分歧影响分析
- 假设有
- 每个 thread blocks 有 8 个 warps(
- 假设有一个
- 每个 thread 将经历 7 个阶段(
- 共有 49 个 thread blocks(每个维度 7 个)
2.3.1 加载 M tiles 时的控制分歧
-
现在共有 42(
-
它们都有 7 个阶段,因此共有 2,352 (
-
warps 只有在最后阶段才有控制分歧
-
因此有 336 个 warp-phases 存在控制分歧
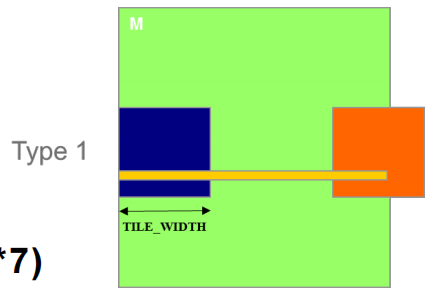
2.3.2 加载 M tiles 时的控制分歧(Type 2)
- Type 2:分配给载入底层 tiles 的 7 个 block,共有 56(
- 它们都有 7 个阶段,因此共有 392(
- 每个 Type 2 block 中有两个 warp 处于 valid range 的边界,包涵控制分歧
- 其余 6 个 warp 不在有效范围内
- 因此,只有 14(
2.3.3 控制分歧的总体影响
- Type 1 Blocks:2,352 个 warp-phases 中有 336 个存在控制分歧
- Type 2 Blocks:392 个 warp-phases 中有 14 个存在控制分歧
- 对性能的影响预计低于
2.3.4 补充
- 计算 N tiles 加载控制分歧的影响略有不同(自行计算)
- 估计的性能影响取决于数据
- 对于较大的矩阵,影响会小得多
- 一般来说,控制分歧对大型输入数据集的边界条件检查影响不大
- 应毫不犹豫地使用边界检查,以确保充分发挥功能
- kernel 充满控制流结构并不意味着会出现大量控制分歧
- 我们将在 "并行算法模式" 模块中介绍一些自然会导致控制分歧的算法模式(如并行缩减)
本文作者:Astron_fjh
本文链接:https://www.cnblogs.com/Astron-fjh/p/18509179
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。


 这篇文章探讨了CUDA编程中的warp和SIMD概念,以及控制分歧对性能的影响。warp是CUDA中线程调度的基本单位,每个warp包含32个线程,以SIMD方式执行相同指令。控制分歧发生在同一warp中线程因不同控制路径而导致执行效率下降。文章通过向量加法示例分析了控制分歧的影响,表明只有在特定情况下(如线程索引超出范围)才会产生控制分歧,其对性能影响通常较小。总体而言,合理设计数据结构和算法可以降低控制分歧,提升CUDA程序的性能。
这篇文章探讨了CUDA编程中的warp和SIMD概念,以及控制分歧对性能的影响。warp是CUDA中线程调度的基本单位,每个warp包含32个线程,以SIMD方式执行相同指令。控制分歧发生在同一warp中线程因不同控制路径而导致执行效率下降。文章通过向量加法示例分析了控制分歧的影响,表明只有在特定情况下(如线程索引超出范围)才会产生控制分歧,其对性能影响通常较小。总体而言,合理设计数据结构和算法可以降低控制分歧,提升CUDA程序的性能。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步