CUDA编程学习 (3)——内存和数据定位

1. CUDA Memories

1.1 GPU 性能如何

所有 thread 都会访问 global memory，以获取输入的矩阵元素
- 在执行一次浮点加法时，需要进行一次内存访问，每次访问传输 4 字节（即 32 位浮点数）
- 1 FLOP（浮点运算）对应 4 字节的内存带宽
假设的 GPU 性能：
- 该 GPU 的峰值浮点计算能力为 1,600 GFLOPS（十亿次浮点运算/秒），内存带宽为 600 GB/s
- 理论上，若要达到 1,600 GFLOPS 的峰值计算能力，需要 4*1,600 = 6,400 GB/s 的内存带宽，但实际内存带宽只有 600 GB/s
性能瓶颈：由于内存带宽的限制，实际执行速度只能达到 150 GFLOPS，这仅仅是 GPU 峰值浮点性能的 9.3%（150/1600）
减少内存访问：为了接近 GPU 的 1,600 GFLOPS 峰值性能，必须大幅减少对内存的访问量。

1.2 示例——矩阵乘法

__global__ void MatrixMulKernel(float* M, float* N, float* P, int Width){
	// Calculate the row index of the P element and M
 	int Row = blockIdx.y * blockDim.y + threadIdx.y;
 	// Calculate the column index of P and N
 	int Col = blockIdx.x * blockDim.x + threadIdx.x;
    
    if ((Row < Width) && (Col < Width)) {
         float Pvalue = 0;
         // each thread computes one element of the block sub-matrix
         for (int k = 0; k < Width; ++k) {
         	Pvalue += M[Row * Width + k] * N[k * Width + Col];
         }
         P[Row * Width + Col] = Pvalue;
	}
}

1.3 thread 到 P 的数据映射

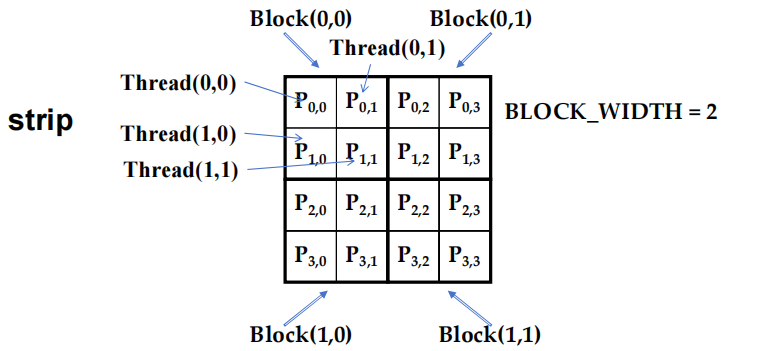
1.4 \(P_{0,0}\) 和 \(P_{0,1}\) 的计算

1.5 程序视角的 CUDA 内存

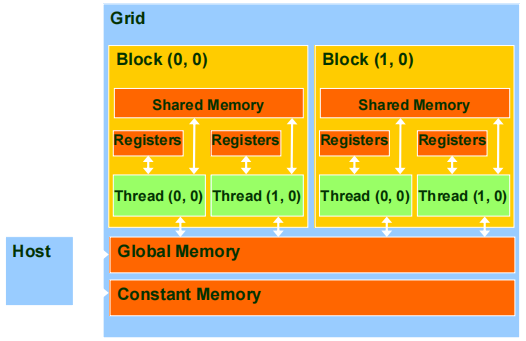
1.5.1 声明 CUDA 变量

当与 __shared__ 或 __constant__ 一起使用时，__device__ 是可选项
自动变量（automatic variables）位于 register 中
- 除位于 global memory 中的 per-thread 数组外

Shared Memory 变量声明：

void blurKernel(unsigned char* in, unsigned char* out, int w, int h){
	__shared__ float ds_in[TILE_WIDTH][TILE_WIDTH];
}

1.5.2 在何处声明变量

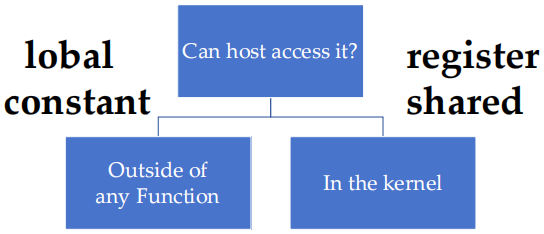
全局（global）声明：在任何函数外部声明的变量，通常是 global memory，可以被所有 thread 访问。host 不能直接访问这些变量，需要通过 device 端操作。
常量（constant）声明：同样是在函数外部声明，但这些变量是只读的，并且通常用于需要在 device 的多个 thread 中共享不变的数据。host 可以访问常量内存，通过 cudaMemcpyToSymbol 等函数将数据从主机拷贝到常量内存。
寄存器（register）声明：在 kernel 函数内部声明，存储在 register 中，属于每个 thread 的私有变量，访问速度非常快。host 不能访问 register 变量。
共享内存（shared）声明：在 kernel 函数内部声明的共享内存，存储在 device 上，可以被同一个 block 中的所有 thread 共享。host 无法直接访问共享内存，只在 device block 内部有效。

1.5.3 CUDA 中的共享内存（Shared Memory）

一种特殊类型的内存，其内容在 kernel 源代码中显式定义并使用

每个 SM（流式多处理器）有一份：每个流式多处理器（SM）都有一块 shared memory 供 block 使用。
高访问速度：与 global memory 相比，访问 shared memory 的速度（延迟和吞吐量）要快得多。
访问范围和共享范围：shared memory 仅在 block 之间共享，并且只能由同一个 block 内的 thread 访问。
生命周期：shared memory 的生命周期仅限于 block，当 block 执行完毕后，内存内容就会消失。
通过加载/存储指令访问：shared memory 通过显式的内存加载和存储指令进行访问。
Scratchpad memory：在计算机架构中，shared memory 可以视为一种临时存储区域，类似于 scratchpad memory。

2. Tiled 并行算法

基本矩阵乘法 kernel 的 global memory 访问模式

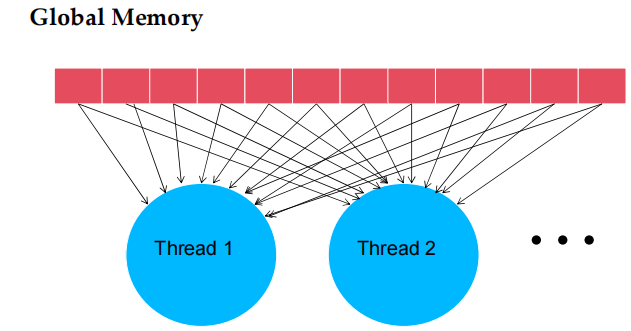
在拥堵的交通系统中，大幅减少车辆数量可以显著改善所有车辆的延迟
- 为通勤者提供拼车服务
- Tiling 用于 global memory 访问
  - 驾驶员 = 访问其内存数据操作数的 thread
  - 汽车 = 内存访问请求

2.1 Tiling 的挑战

有些拼车可能比其他拼车更容易：有些计算任务的 Tiling 更容易，而有些则较难
拼车的参与者需要有类似的工作时间表：就像拼车中的乘客需要有相似的时间安排一样，在 thread 并行处理中，任务需要有相似的计算特征或数据访问模式才能有效使用 Tiling
拼车需要同步
- Good：当人们的日程安排相似时
- - Bad：当人们的日程安排大相径庭时
Tiling 也是一样
- Good：当 thread 具有相似的访问时序时
- Bad：当 thread 的时间非常不同时

2.2 Tiling 技术概要

识别一个由多个 thread 访问的 global memory tile：找到 global memory 中的一个 tile 数据，这个 tile 数据将会被多个 thread 同时访问
将这个 tile 从 global memory 加载到片上 memory：把这个 tile 数据从 global memory 中移到片上更快的memory（如shared memory）中
使用屏障同步确保所有 thread 都准备好开始当前阶段：通过同步机制，确保所有 thread 都达到了一个同步点，准备好下一步操作
让多个 thread 从片上 memory 中访问它们的数据：所有 thread 从这个更快速的片上 memory 中读取数据，避免重复访问慢速的 global memory
再次使用屏障同步确保所有 thread 完成当前阶段：确保所有 thread 都完成了当前阶段的工作，避免提前进入下一步
**继续处理下一个 tile **：一旦当前 tile 的处理完成，重复上述步骤处理下一个 tile

3. Tiled 矩阵乘法

3.1 矩阵乘法

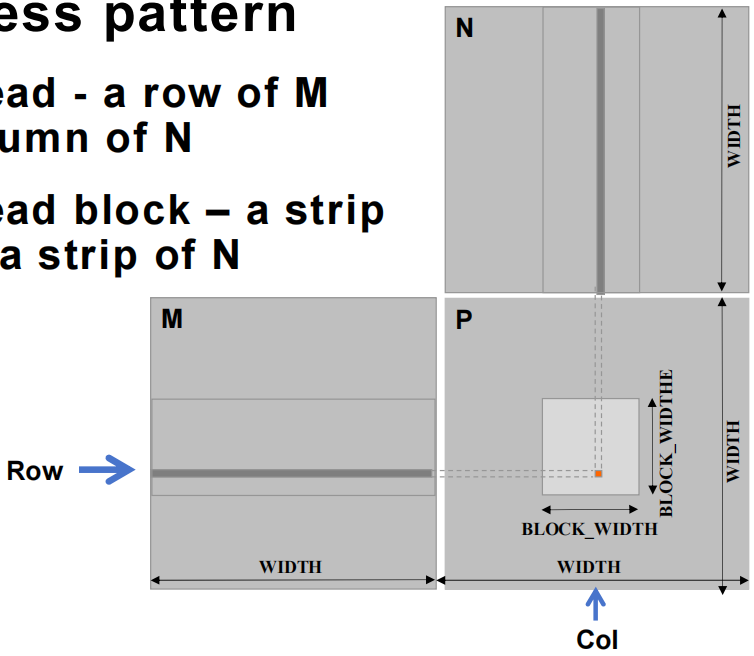
数据访问模式
- 每个 thread - 负责矩阵 \(M\) 的一行和矩阵 \(N\) 的一列的计算。这意味着每个 thread 会处理两个矩阵的部分数据，以完成其对应位置的矩阵乘积结果。
- 每个 thread block - 负责矩阵 \(M\) 的一条 “带状（strip）” 区域和矩阵 \(N\) 的一条 “带状（strip）” 区域的计算。这指的是，thread block 并不是处理整个矩阵，而是划分矩阵成多条 “带状（strip）” 形式，每个 thread block 处理其中的一部分，以提高计算的并行度。

3.2 Tiled 矩阵乘法

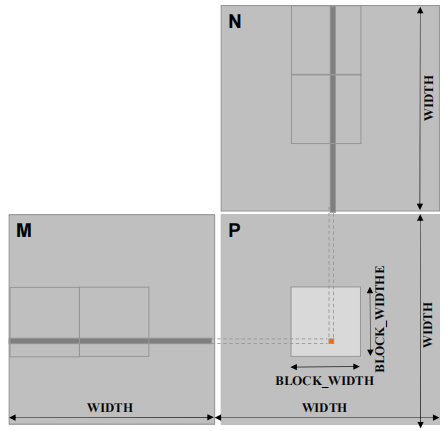
将每个 thread 的执行分成几个阶段
thread block 在每个阶段的数据访问都集中在 M 的一个 tile 和 N 的一个 tile 上
这些 tile 的大小是每个维度中 BLOCK_SIZE 的元素数量。

3.3 加载 Tile

block 中的所有 thread 都参与加载：每个 block 中的所有 thread 共同完成 tile 的数据加载任务
- 每个 thread 负责加载一个 M 矩阵元素和一个 N 矩阵元素

阶段 0 的 Block(0,0) 加载

阶段 0 的 Block(0,0) 计算 (iteration 0)

阶段 0 的 Block(0,0) 计算 (iteration 1)

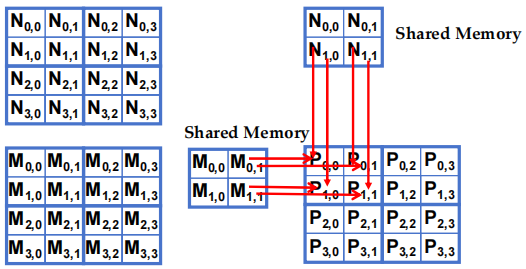
阶段 1 的 Block(0,0) 加载

阶段 1 的 Block(0,0) 计算 (iteration 0)

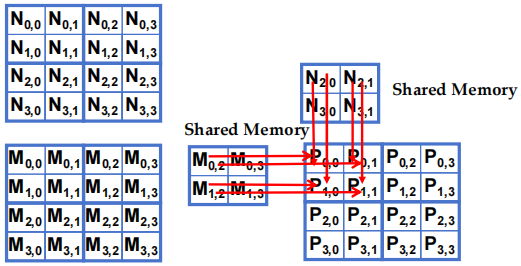
阶段 1 的 Block(0,0) 计算 (iteration 1)

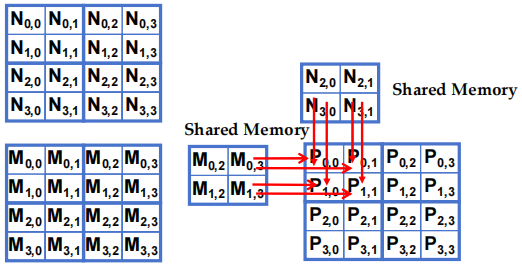
执行阶段

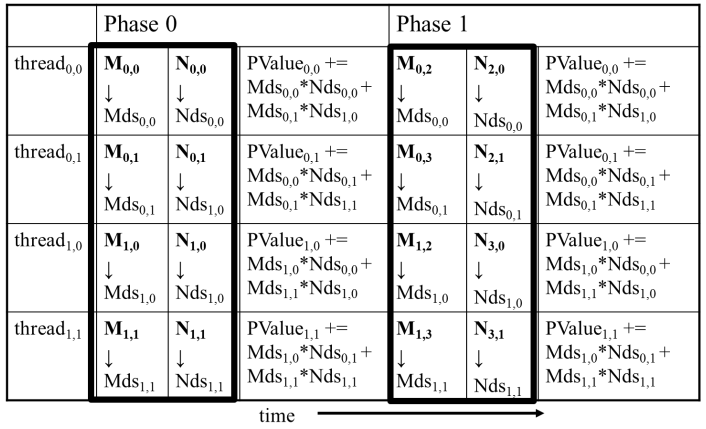
3.4 障碍同步（Barrier Synchronization）

同步 block 中的所有 thread：通过同步机制，确保 block 中的所有 thread 在继续执行前都处于同一进度。

__syncthreads()：在同一个 block 中的所有 thread 必须在到达 __syncthreads() 后，才能继续执行后续的指令。这意味着，thread 只有在所有 thread 到达同步点时，才能同时继续。
最佳用法是协调分阶段执行的分 tile 算法：__syncthreads() 最适用于分 tile 算法的阶段性执行，确保所有 thread 在正确的时间协同工作。
- 确保 tile 中的所有元素在每个阶段开始时被加载：使用 __syncthreads() 确保在每个阶段开始时，tile 内的所有元素都已经加载完毕。
- 确保 tile 中的所有元素在每个阶段结束时被使用：使用 __syncthreads()确保在进入下一阶段之前，当前阶段的所有数据都被 thread 处理完毕。

4. Tiled 矩阵乘法 kernel

4.1加载 M、N 的输入 Tile 0（阶段 0）

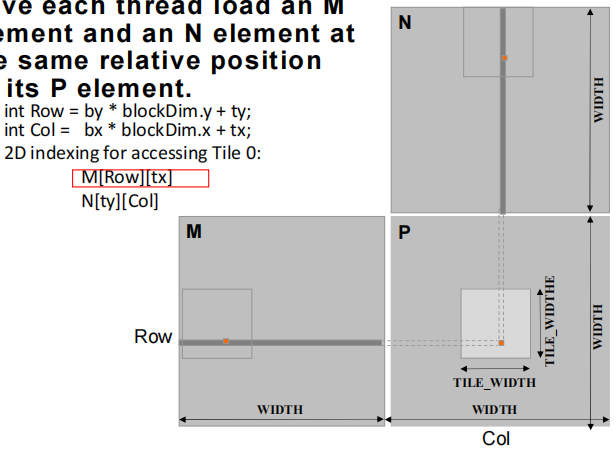
int Row = by * blockDim.y + ty
int Col = bx * blockDim.x + tx
对矩阵M：M[Row][tx]
对矩阵N：N[ty][Col]

by 和 bx 是块的索引，分别对应Y和X方向的块。

blockDim.y 和 blockDim.x 是每个块中的线程数量，ty 和 tx 是线程在当前块中的局部索引。

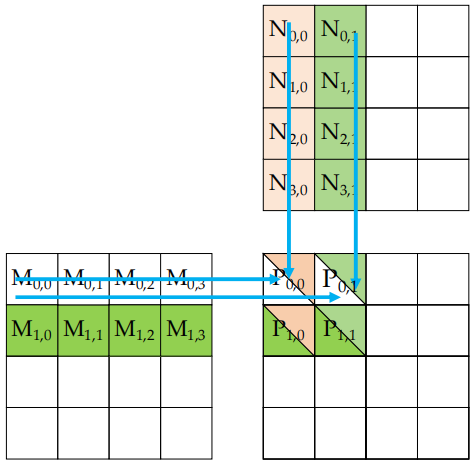
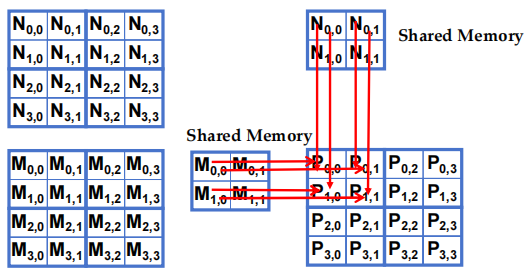
每个 thread 从M和N矩阵中加载与其P矩阵元素相对应的元素。图示中：

M和N的整个矩阵以方块形式显示，每个方块中的点表示 thread 正在处理的元素。
P矩阵的一个小块正被计算，每个 thread 会从M和N中选取对应的元素来参与计算。

4.2 加载 M、N 的输入 Tile 1（阶段 1）

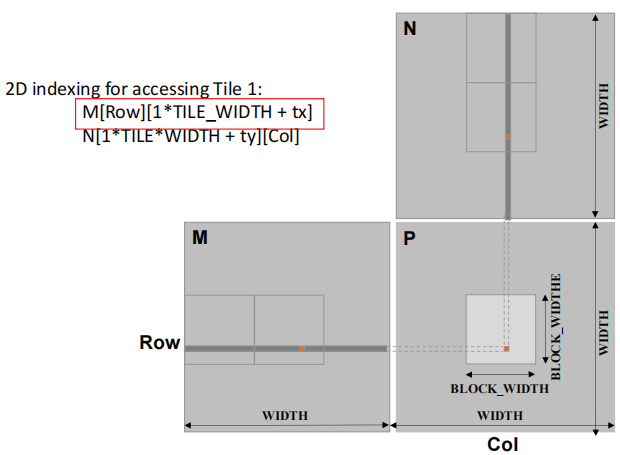
对矩阵M：M[Row][1*TILE_WIDTH + tx]
对矩阵N：N[1*TILE_WIDTH + ty][Col]

4.3 M 和 N 是动态分配的——使用 1D 索引

M[Row][p * TILE_WIDTTH + tx] -> M[Row * WIDTH + p * TILE_WIDTH + tx]
N[p * TILE_WIDTH + ty][Col] -> N[(p * TILE_WIDTH + ty) * WIDTH + Col]

其中，p 是当前阶段的序列号

4.4 Tiled 矩阵乘法 kernel

__global__ void MatrixMulKernel(float* M, float* N, float* P, int Width)
{
    __shared__ float ds_M[TILE_WIDTH][TILE_WIDTH];
	__shared__ float ds_N[TILE_WIDTH][TILE_WIDTH];
    
    int bx = blockIdx.x;
    int by = blockIdx.y;
 	int tx = threadIdx.x;
    int ty = threadIdx.y;
    
    int Row = by * blockDim.y + ty;
	int Col = bx * blockDim.x + tx;
 	float Pvalue = 0;
    
    // 循环计算 P 元素所需的 M 和 N tile
    for (int p = 0; p < n/TILE_WIDTH; ++p){
    	// 将 M 和 N tile 协同载入 shared memory
        ds_M[ty][tx] = M[Row*WIDTH + p*TILE_WIDTH + tx];
        ds_N[ty][tx] = N[(p*TILE_WIDTH + ty)*WIDTH + Col];
        __syncthreads();
        
        for (int i = 0; i < TILE_WIDTH; ++i)
            Pvalue += ds_M[ty][i] * ds_N[i][tx];
        __synchthreads();
    }
    P[Row * Width + Col] = Pvalue;
}

4.5 Tile（Thread Block）大小

每个 thread block 应包含多个 thread

如果 TILE_WIDTH 有 16，则有 \(16*16 = 256\) threads
如果 TILE_WIDTH 有 32，则有 \(32*32 = 1024\) threads

对于 16，在每个阶段，每个 block 从 global memory 执行 \(2*256 = 512\) 次浮点加载，进行 \(256 * (2*16)=8,192\) 次乘加操作。(每个 memory 加载 16 次浮点运算）

对于 32，在每个阶段，每个 block 从 global memory 执行 \(2*1024 = 2048\) 次浮点加载，进行 \(1024 * (2*32) = 65,536\) 次乘加操作。(每个 memory 加载 32 次浮点运算）

4.6 Shared Memory 和 Threading

对于具有 16KB shared memory 的 SM

shared memory 大小取决于执行情况
TILE_WIDTH = 16 时，每个 thread block 使用 \(2*256*4\ Byte = 2K\ Byte\) （一个 \(16*16\) 的 M 和一个 \(16*16\) 的 N，其中一个元素占据 4 Byte）的 shared memory
对于 16KB shared memory，最多可能有 8 个 thread block 在执行
- 这允许多达 \(8*2*256=4,096\) 个待加载。(每个线程有 2 个，每个区块有 256 个线程）
下一个 TILE_WIDTH 为 32，将导致每个 thread block 使用 \(2*32*32*4\ Byte=8K\ Byte\) 的 shared memory，允许 2 个 thread block 同时工作
- 然而，在 GPU 中，每个 SM 的 thread 数限制为 1536 个，因此每个 SM 的 block 数减少为一个！

每个 __syncthread() 都能减少一个 block 的活动 thread 数

更多的 thread blocks 可能更有优势

5. 在 Tiled 算法中处理任意大小矩阵

5.1 处理任意大小的矩阵

到目前为止，我们介绍的 tiled 矩阵乘法 kernel 只能处理尺寸（Width）是 tile 宽度（TILE_WIDTH）倍数的正方形矩阵。

然而，实际应用需要处理任意大小的矩阵。
我们可以将 row 和 column 填充（添加元素）为 tile 大小的倍数，但这将产生巨大的空间和数据传输时间开销。我们将采取不同的方法。

5.1.1 阶段 1 加载 3x3 的 Block(0,0)

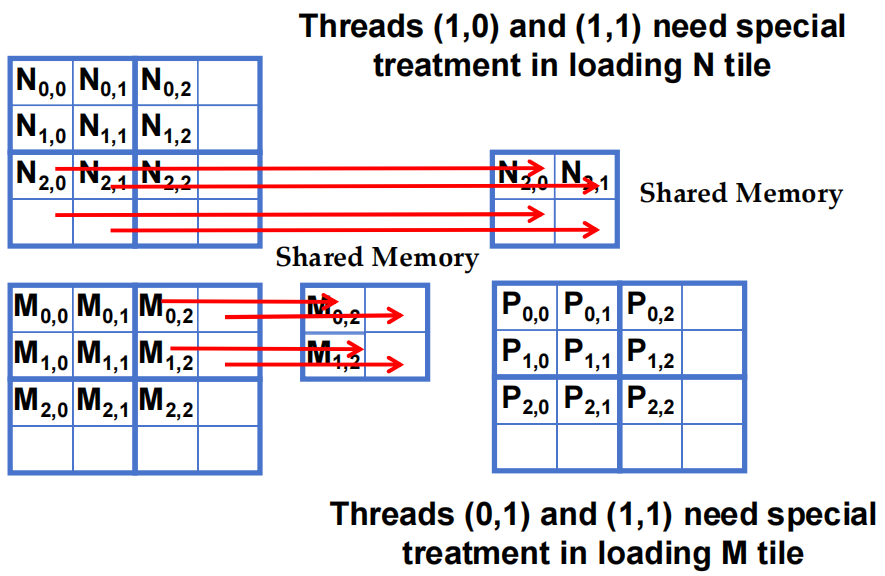
在加载 N tile 时 Threads (1,0) 和 (1,1) 需要特殊处理
在加载 M tile 时 Threads (0,1) 和 (1,1) 需要特殊处理

5.1.2 阶段 1 的 Block(0,0) 计算 (iteration 0)

5.1.3 阶段 1 的 Block(0,0) 计算 (iteration 1)

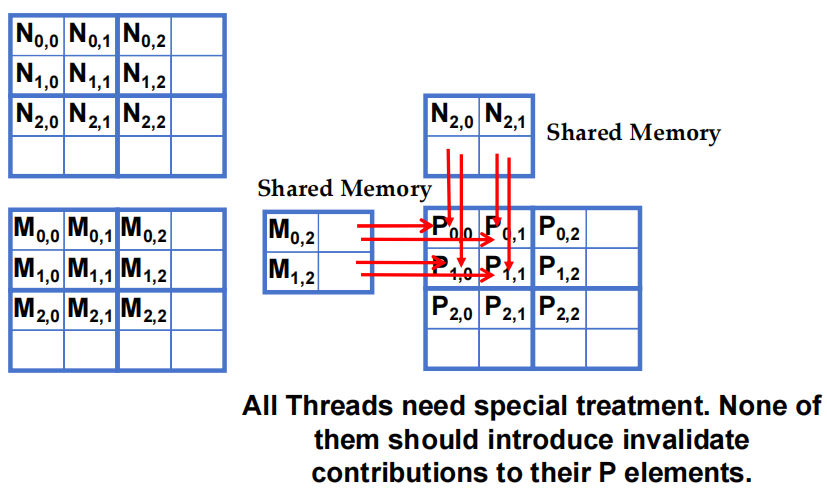
所有 thread 都需要特殊处理，所有 thread 都不应为其 P 元素引入无效贡献。

5.1.3 阶段 0 加载 3x3 的 Block(1,1)

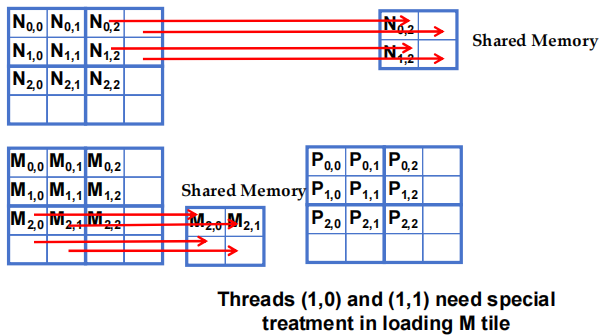
Thread(1,0) 和 (1,1) 在加载 M tile 时需要特殊处理

5.1.4 上述例子的要点

不计算有效P元素的 thread：
- 即使某些 thread 不直接计算有效的输出矩阵 P 的元素，它们仍然需要参与加载输入矩阵的 tile 数据。
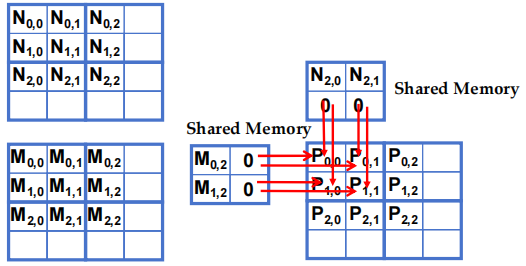
- 例子1：Block(1,1) 的 Phase 0 阶段：
  - Thread(1,0) 被分配去计算一个不存在的P矩阵元素 P[3,2]，但仍需参与加载输入矩阵N的元素 N[1,2]。
  - 这意味着，即使这个 thread 不会直接计算 P 中的有效结果，它仍需要协助完成输入数据（这里是N矩阵）的加载。
计算有效P元素的 thread：
- 即使某些 thread 被分配去计算有效的 P 矩阵元素，它们在加载输入数据时可能会尝试加载不存在的元素。
- 例子2：Block(0,0) 的 Phase 0 阶段：
  - Thread(1,0) 被分配去计算有效的 P 矩阵元素 P[1,0]，但在加载输入时，它可能尝试去加载不存在的N矩阵元素 N[3,0]。

5.1.5 简单的解决方法

当 thread 要加载任何输入元素时，测试该元素是否在有效索引范围内
- 如果有效，则继续加载
- 否则，不加载，只写入 0
理由：0 值将确保乘加步骤不会影响输出元素的最终值
加载输入元素时测试的条件，与计算输出 P 元素时测试的条件不同
- 即使一个 thread 不计算有效的 P 元素，它仍然可以参与加载输入数据块的元素
阶段 1 的 Block(0,0) 计算 (iteration 1)

5.2 边界条件

5.2.1 输入 M tile 的边界条件

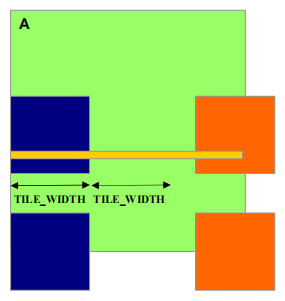
每个线程加载
- M[Row][p*TILE_WIDTH + tx]
- M[Row*WIDTH + p*TILE_WIDTH + tx]
需要进行测试
- (Row < Width) && (p*TILE_WIDTH + tx < WIDTH)
- 如果为 true，加载 M 元素
- 否则，加载 0

5.2.2 输入 N tile 的边界条件

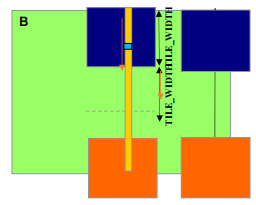
每个线程加载
- N[p*TILE_WIDTH + ty][Col]
- N[(p*TILE_WIDTH + ty)*WIDTH + col]
需要进行测试
- (p*TILE_WIDTH + ty < WIDTH) && (Col < WIDTH)
- 如果为 true，加载 N 元素
- 否则，加载 0

5.2.3 加载元素 - 带边界检查

for(int p = 0; p < (WIDTH-1) / TILE_WIDTH + 1; ++p){
    if(Row < WIDTH && p*TILE_WIDTH + tx < WIDTH){
        ds_M[ty][tx] = M[Row*WIDTH + p*TILE_WIDTH + tx];
    } else {
        ds_M[ty][tx] = 0.0;
    }
    
    if(p*TILE_WIDTH + ty < WIDTH && Col < WIDTH){
        ds_N[ty][tx] = N[(p*TILE_WIDTH + ty) * WIDTH + Col];
    } else {
        ds_N[ty][tx] = 0.0;
    }
    __syncthreads();
    
    if(Row < WIDTH && Col < WIDTH) {
    	for(int i = 0; i < TILE_WIDTH; ++i) {
        	Pvalue += ds_M[ty][i] * ds_N[i][tx];
        }
        __syncthreads();
    }
    if (Row < WIDTH && Col < WIDTH) 
		P[Row*WIDTH + Col] = Pvalue;
}

5.2.4 一些重点

每个 thread 的条件都不同

加载 M 元素
加载 N 元素
计算并存储输出元素

5.2.5 处理一般矩形矩阵

一般来说，矩阵乘法是用矩形矩阵定义的：

\(j \times k\) \(M\) 矩阵与 \(k \times l\) \(N\) 矩阵相乘，得到 \(j \times l\) \(P\) 矩阵

上面我们介绍了正方形矩阵乘法，这是一种特殊情况。

kernel 函数需要通用化，以处理一般矩形矩阵：

Width 参数由三个参数代替：j、k、l
当 Width 用于指 M 的高度或 P 的高度时，用 j 代替
当 Width 用于指 M 的宽度或 N 的高度时，用 k 代替
当 Width 用于指 N 的宽度或 P 的宽度时，用 l 代替

posted @ 2024-10-27 22:48 Astron_fjh 阅读(9) 评论(0) 编辑收藏举报

刷新页面返回顶部

Astron-fjh