[可能有用科技]后缀树
前言
参考 : 2021 年信息学奥林匹克中国国家集训队论文 代晨昕 后缀树的构建
似乎后缀树可以在一些题目代替 SAM 套 LCT 啊.
妈妈再也不怕我考场写不出LCT了
后缀树也写不出啊.
反正能写进国集论文的东西一定不会差(?)
约定
\(s\) : 表示要建立后缀树 / 要对其求解的字符串.
\(n\) : \(|s| = n\) , 即字符串长度.
子串 : 字符串 \(s\) 中的一个连续段,如无说明,默认为非空的子串.
\(s[l,r]\) : 字符串 \(s\) 从 \(s_l\) 到 \(s_r\) 的子串,一般地,\(l \le r\).
\(s[1,i]\) : 字符串以 \(i\) 结尾的前缀.
\(s[i,n]\) : 字符串以 \(i\) 开头的后缀.
\(\Sigma\) : 字符集.
\(|\Sigma|\) : 字符集大小.
\(\mathrm{STree(s)}\) : 字符串 \(s\) 的隐式后缀树.
\(\mathrm{mx}_i\) : 一个结点 \(i\) 对应等价类中最长的串.
\(\mathrm{len}_i\) : \(|\mathrm{mx}_i|\)
从后缀 Tire 开始
首先直接非常 \(naive\) 地把字符串所有后缀都插入一个 Trie 里.
时空复杂度 \(\mathcal{O} (n^2)\),是个人都能看出但凡把数据出大一点就寄了.
于是先看一下后缀 Tire 有什么不合理的地方 :
太多的结点前的转移仅仅是一条链,浪费大量空间.
考虑把 拥有多于一个儿子的结点 和 叶子结点 作为关键点.
建立只保留关键点和后缀,将非关键点压缩为一条边的 Trie 称作 后缀树.
建立只保留关键点的经过信息压缩的 Trie 称为 隐式后缀树.
举个例子,对于 cabab 建立上述三者 :
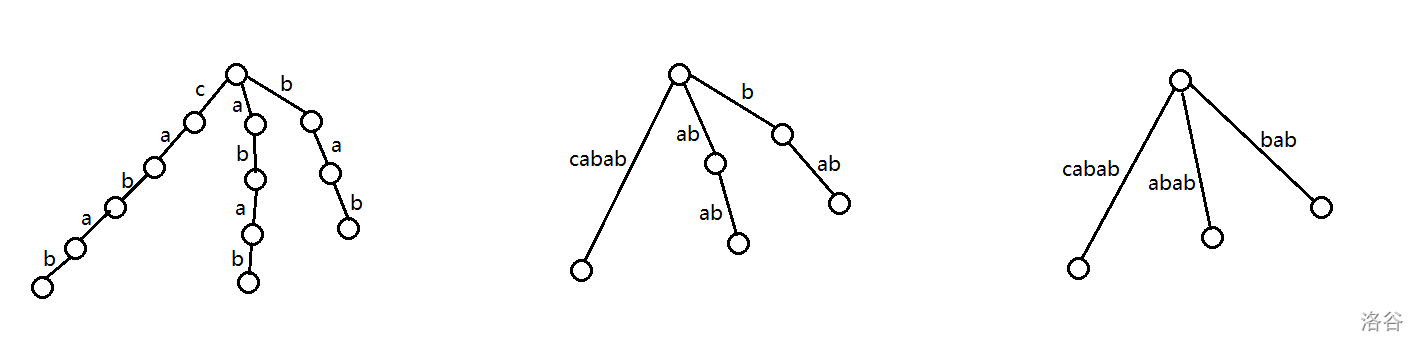
(图片来自 代晨昕论文,三者分别为 后缀 Trie,后缀树,隐式后缀树)
可以发现后缀树比隐式后缀树多了两个点,因为那两个点在隐式后缀树的关键点定义下不算关键点,但是是一个后缀结点,于是在后缀树中可以单独出现.
后缀树的构建
支持前端动态添加字符的算法
众所周知对于反串建 SAM 建出的 parent 树就是这个串的后缀树,那么我们得到了一个线性建立后缀树的在线方法,甚至支持前端添加字符.
Code :
倒着调用 extend() 即可.
struct SuffixAutomaton {
int tot,lst;
int siz[N << 1];
int buc[N],id[N << 1];
struct Node {
int len,link;
int ch[26];
}st[N << 1];
SuffixAutomaton() : tot(1),lst(1) {}
inline void extend(int ch) {
int cur = ++tot,p = lst;lst = cur;
siz[cur] = 1,st[cur].len = st[p].len + 1;
for(;p && !st[p].ch[ch];p = st[p].link)
st[p].ch[ch] = cur;
if(!p) st[cur].link = 1;
else {
int q = st[p].ch[ch];
if(st[q].len == st[p].len + 1)
st[cur].link = q;
else {
int pp = ++tot;st[pp] = st[q];
st[pp].len = st[p].len + 1;
st[cur].link = st[q].link = pp;
for(;p && st[p].ch[ch] == q;p = st[p].link)
st[p].ch[ch] = pp;
}
}
}
}SAM;
支持后端动态添加字符的 Ukkonen 算法
Ukkonen 算法是能够在线性时间构造一个字符串的 隐式后缀树 的在线算法.
通过上面的图和隐式后缀树的定义我们能够知道隐式后缀树的每个结点都对应原串 \(s\) 的一个后缀,但是并不是所有后缀都被包括在内.
将 \(\mathrm{STree(s)}\) 中不作为结点出现的后缀称为 隐式后缀,与其相对的,出现了的称为 显式后缀.
Lemma : 有 \(s\) 的隐式后缀 \(s[i,n]\),那么 \(\forall j > i,s[j,n]\) 是 \(s\) 的隐式后缀.
证明 : \(s[i,n]\) 为隐式后缀,说明其原本的后缀结点不是叶子结点,即存在一个字符 \(c \in \Sigma\) 使得 \(s[i,n] + c\) 是 \(s\) 的子串.
而因为 \(s[j,n]\) 是 \(s[i,n]\) 的子串, \(s[j,n] + c\) 一定也在 \(s\) 中作为子串出现, \(s[j,n]\) 的后缀结点不是叶子结点,其在隐式后缀树上是不出现的.
于是可以发现隐式后缀是那些被包含了的短后缀.
考虑在结尾添加字符会影响什么.
在后缀 Trie 上新增结点,这是显然的.
隐式后缀树上,这只导致显式后缀父边增长,而主要影响的是隐式后缀.
现在我们维护一个重要的三元组 \((k,active,remain)\) 表示 \(s[k,n]\) 是目前最长的隐式后缀,其所属结点的父节点为 \(active\),位置为从 \(active\) 向下走 \(remain\) 步.
后缀链接
和 SAM 的后缀链接意思差不多.
Lemma : 对于隐式后缀树的一个非根非叶结点 \(x\),总有一结点 \(y\) 使得 \(c + mx_y = mx_x\),其中 \(c\) 是一个字符.
证明 : 首先 \(x\) 能在隐式后缀树出现,则必定有 \(mx_x + c_1\) 和 \(mx_x + c_2\ (c_1,c_2 \in \Sigma)\) 这两个串是 \(s\) 的子串使得 \(x\) 作为一个分歧点.
于是 \(mx_y\) 也有 \(mx_y + c_1\) 和 \(mx_y + c_2\) ,可知 \(mx_y\) 是显然存在切作为独立结点的.
现在就将上面这个引理中所描述的 \(x,y\) 关系定义为 :
\(\mathrm{Link}(x) = y\).
算法流程
采取增量法.
对于一个字符串 \(s\),考虑已经完成 \(s[1,m] (m < n)\) 的情况下如何添加一个字符 \(x = s[m + 1]\).
首先是对于构造的串的影响,从字符串的角度来说,每个后缀延长一个字符且增加一个新的后缀.
每个显式后缀都是叶结点,那么只会使得显式后缀父边增长.
现在考虑对隐式后缀的影响.
-
\((k,active,remain)\) 位置无需新增出边,那么原后缀树形态不变, \(remain\) 加 \(1\).
-
\((k,active,remain)\) 位置需要新增出边.
如果 \(active\) 不是根节点,考虑通过 \(\mathrm{Link}\) 向上跳,否则 \(reamin - 1\),最后 \(k\) 需要加 \(1\).
下面具体说一下情况 2 的过程 :
首先像 SAM 一样维护一个 \(lst\) 方便找到上个位置.
然后从长到短找每个隐式后缀 \(sub\).
- 如果 \(sub + x\) 已经在 \(\mathrm{STree}\) 里了,且 \(lst\) 存在,那么 \((k,active,remain)\) 位置为一个非叶结点.
此时找到的点即为 \(\mathrm{Link}(lst)\),然后 \(remain + 1\) 即可退出迭代.
- 如果 \(sub + x\) 不在 \(\mathrm{STree}\) 里,需要新建结点.
从当前结点连向新节点,\(\mathrm{Link}(lst)\)即为当前结点,把当前结点设为 \(lst\).
退出迭代后,如果 \(active\) 不是根节点,考虑通过 \(\mathrm{Link}\) 向上跳,否则 \(reamin - 1\).
Code :
struct SuffixTree {
int link[N << 1],len[N << 1];
int st[N << 1],s[N];
int ch[N << 1][27];
int n,tot,cur,rem;
SuffixTree() : tot(1),cur(1) {len[0] = INF;}
inline int NewNode(int pos,int l) {
link[++tot] = 1;
st[tot] = pos;
len[tot] = l;
return tot;
}
inline void extend(int x) {
s[++n] = x,++rem;
for(int lst = 1;rem;) {
while(rem > len[ch[cur][s[n - rem + 1]]])
rem -= len[cur = ch[cur][s[n - rem + 1]]];
int &v = ch[cur][s[n - rem + 1]];
int c = s[st[v] + rem - 1];
if(!v || x == c) {
link[lst] = cur;lst = cur;
if(!v) v = NewNode(n,INF);
else break;
}
else {
int u = NewNode(st[v],rem - 1);
ch[u][c] = v,ch[u][x] = NewNode(n,INF);
st[v] += rem - 1,len[v] -= rem - 1;
link[lst] = v = u;lst = u;
}
if(cur == 1) --rem;
else cur = link[cur];
}
}
}T;
后缀树的应用
如果套回滚莫队是不是可以做 这个题 啊.

