八种(?)方法求平方和的通项

前言#

本博客部分参考 《具体数学》 一书.

本博客 基本 不需要任何高于初中数学的前置知识.

本博客作者数学很差,若有笔误请第一时间指正.

本博客的数学公式加了 \large,看起来不会很挤,为了保护你的视力,请在电脑上阅读.

问题#

定义

$$\large sq_n = \sum_{i = 1}^{n} i^2$$

求 $sq_n$ 的通项.

方法 0#

要善于利用你的搜索引擎.

链接

于是可知 , 通项为 :

$$\large sq_n = \frac{n(n + 1)(2n + 1)}{6}$$

方法 1#

这么个数列问题,首先考虑打个表.

$n$	0	1	2	2	4	5	6	7	8	9	10	11	12
$sq_n$	0	1	5	14	30	55	91	140	204	285	385	506	650

我们不妨构造一个函数$f(x)$，使得：

$$\large \begin{aligned} f(0)=0 \\ f(1)=1 \\ f(2)=5 \\ f(3)=14 \\ f(4)=30 \\ f(5)=55 \\ f(6)=91 \\ f(7)=140 \\ f(8)=204 \\ f(9)=285 \\ f(10)=385 \\ f(11)=506 \\ f(12)=650 \\ \end{aligned}$$

易得：

$$\large\begin{aligned} f(x)= &\frac{22739}{1245404160} x^{13} \\&-\frac{22739}{15966720} x^{12} \\&+\frac{432041}{8709120} x^{11} \\&-\frac{295607}{290304} x^{10} \\&+\frac{39725033}{2903040} x^{9} \\&-\frac{6798961}{53760} x^{8} \\&+\frac{7154075963}{8709120} x^{7} \\&-\frac{1092267865}{290304} x^{6} \\&+\frac{26126269657}{2177280} x^{5} \\&-\frac{9368672651}{362880} x^{4} \\&+\frac{2932835723}{83160} x^{3} \\&-\frac{150461191}{5544} x^{2} \\&+\frac{682183}{78} x \end{aligned}$$

其中：

$$\large \begin{aligned} f(13)=114514 \\ \end{aligned}$$

所以，应填入空缺处的数字依次为：$114514$.

大雾.

但是,观察力像 神 $\mathrm{\color{black}{w}\color{red}{ind\_whisper}}$ 一样强的的人能看出,其通项是

$$\large sq_n = \frac{n(n + 1)(2n + 1)}{6}$$

那么考虑如何证明,采取 归纳法.

基础 : 对于 $n = 0$ ,$sq_0 = \frac{0}{6} = 0$ , 成立.

归纳 :

首先为了看着舒服把式子稍微变一下 :

$$\large sq_n = \frac{n(n + 1)(n + \frac{1}{2})}{3}$$

然后写出递归式 :

$$\large\boxed{\begin{aligned} &sq_0 = 0,sq_1 = 1\\ &sq_n = sq_{n - 1} + n ^ 2 \end{aligned}}$$

两侧乘 3 :

$$\large\begin{aligned} 3 sq_n &= 3 sq_{n - 1} + 3n ^ 2\\ &= (n - 1)(n - 1 - \frac{1}{2})(n - 1 + 1) + 3n^2\\ &= n^3 + \frac{3}{2}n^2 + \frac{n}{2}\\ &=n(n^2 + \frac{3}{2}n + \frac{1}{2})\\ &= n(n + 1)(n + \frac{1}{2}) \end{aligned}$$

成立.

但是每次有类似问题都嗯猜属实拉跨,下面会介绍更泛用的方法,都以求平方和通项作为例子.

方法 2#

扰动法 :

$$\large\begin{aligned} sq_{n + 1} &= \sum_{i = 1}^{n + 1} i^2 \\ sq_n + (n^2 + 2n + 1) &= \sum_{i = 0}^{n} (i + 1)^2\\ &= \sum_{i = 0}^{n} (i ^ 2 + 2i + 1)\\ &= \sum_{i = 1}^{n} i^2 + 2\sum_{i = 0}^{n} (i + n + 1)\\ &= sq_n + n(n + 1) + n + 1 \end{aligned}$$

可以发现又推回去了,如蜜传如蜜啊.

但是发现把 $sq_n$ 消掉后得到了求 $\sum_{i = 1}^{n} i$ 的通项,也就是低一次的通项.

那么把要求的升级一下,定义 :

$$\large cub_n = \sum_{i = 1}^{n} i^3$$

考虑通过这个求出 $sq_n$ 的通项.

$$\large\begin{aligned} cub_{n + 1} &= \sum_{i = 1}^{n + 1} i^3\\ cub_n + (n + 1)^3 &= \sum_{i = 0}^{n} (i + 1)^3\\ &= \sum_{i = 0}^{n} (i ^3 + 3i^2 + 3i + 1)\\ &= cub_n + 3sq_n + 3\cdot \frac{n(n + 1)}{2} + (n + 1) \end{aligned}$$

然后把 $cub_n$ 消掉再移项就是通项了.

方法3#

gg 说 : 格局打开.

现在直接把格局开大,直接推广这类递推式.

考虑建立一般模型 :

$$\large\begin{aligned} R_0 &= \alpha\\ R_n &= R_{n - 1} + \beta + \gamma n + \delta n^2 \end{aligned}$$

将其解表示为 :

$$\begin{aligned} R_n = A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta \end{aligned}$$

然后 $A(x),B(x),C(x),D(x)$ 和生成函数啥关系没有,别想多了.

首先,假设对于 $R_n = 1$,有 :

$$\large\begin{aligned} &A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = 1\\ &\therefore \alpha = 1,\beta = 0,\gamma = 0,\delta = 0. \therefore A(n) = 1 \end{aligned}$$

然后假设 $R_n = n$, 有 :

$$\large\begin{aligned} &A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = n\\ &\therefore \alpha = 0,\beta = 1,\gamma = 0,\delta = 0. \therefore B(n) = n \end{aligned}$$

然后假设 $R_n = n^2$,有 :

$$\large\begin{aligned} &A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = n^2\\ &\therefore \alpha = 0,\beta = -1,\gamma = 2,\delta = 0. \therefore 2C(n) - B(n) = n^2\\ &\therefore C(n) = \frac{n(n + 1)}{2} \end{aligned}$$

然后假设 $R_n = n^3$,有 :

$$\large\begin{aligned} &A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = n^3\\ &\therefore \alpha = 0,\beta = 1,\gamma = -3,\delta = 3. \therefore 3D(n) - 3C(n) + B(n) = n^3\\ &\therefore D(n) = \frac{n(n + 1)(n + \frac{1}{2})}{3} \end{aligned}$$

这时候考虑原来的递推式,相当于$\alpha = \beta = \gamma = 0,\delta = 1$ 的特殊情况,那么 :

$$\large sq_n = D(n) = \frac{n(n + 1)(n + \frac{1}{2})}{3}$$

方法 4#

考虑 积分 .

首先,为了方便贴近我们要求的合式,积分可以形象化理解成求一个函数与 $x$ 轴之间封闭图形的面积.

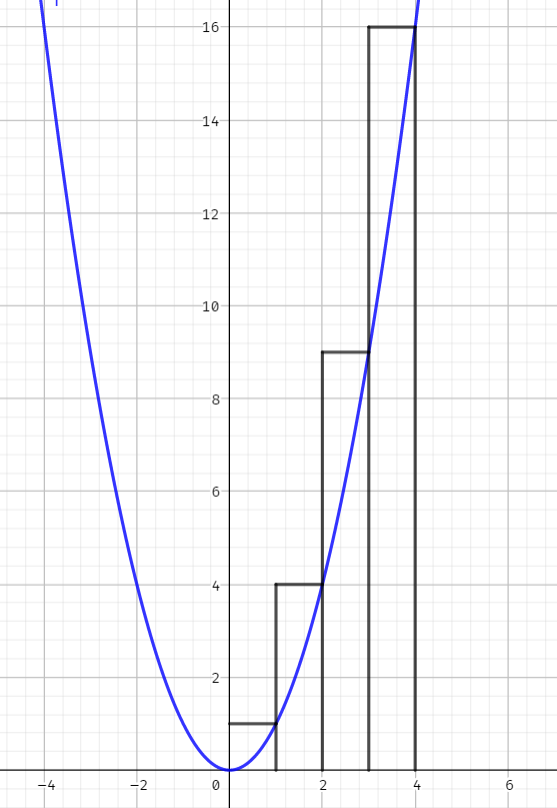
我们要求的是图中每个矩形面积的和,而图中蓝色 (是(0,0,255),别说什么你是全色盲,自己拿取色器看) 的抛物线是 $y = x^2$ ,可以发现误差不大,考虑积分计算抛物线以下部分的面积.

然后用小学二年级(?)就有人告诉你的如下公式 :

$$\large\begin{aligned} \int x^\mu dx = \frac{x^{\mu + 1}}{\mu + 1} + C ,(\mu \neq -1) \end{aligned}$$

得出 :

$$\large sq_n \approx \int_{0}^{n} x^2 dx = \frac{n^3}{3}$$

然后要求更精确的解,就需要单独计算误差面积.

定义 :

$$\large E_n = sq_n - \frac{n^3}{3}$$

那么代入递推式 :

$$\large\begin{aligned} E_n &= sq_n - \frac{n^3}{3}\\ &= sq_{n - 1} + n^2 - \frac{n^3}{3}\\ &= E_{n - 1} +\frac{1}{3} (n - 1)^3 + n^2 - \frac{n^3}{3}\\ &= E_{n - 1} + n - \frac{1}{3} \end{aligned}$$

最后解出来 :

$$\large E_n = \frac{3n^2 + n}{6}$$

那么

$$\large sq_n = E_n + \int_{0}^{n} x^2 dx = \frac{n(n + 1)(2n + 1)}{6}$$

此方法最好的一点是求近似解可以推广 :

$$\large \sum_{i = 1}^{n} i^k \approx \int_{0}^{n} x^k dx = \frac{x^{k + 1}}{k + 1}$$

方法 5#

奇怪的技巧之 : 展开和收缩 .

从加法展开后的形式上理解一下原本的合式 :

$$\large\begin{aligned} \sum_{i = 1}^{n} (i \cdot i) &= (1 \cdot 1) + (2 \cdot 2) + \cdots + (n \cdot n) \\ &= 1 + 2 + 2 + 3 + 3 + 3 + \cdots + n + n + \cdots + n\\ &= \sum_{1 \le j \le i \le n} i\\ &= \sum_{j = 1}^{n} \sum_{i = j}^{n} i\\ &= \sum_{j = 1}^{n} \frac{(j + n)(n - j + 1)}{2}\\ &= \frac{1}{2} \sum_{j = 1}^{n} (n(n + 1) + j - j^2)\\ &= \frac{1}{2} n^2(n + 1) + \frac{1}{4}n(n + 1) - \frac{1}{2} sq_n \end{aligned}$$

然后依然是移项即可求解.

或者如果你知道的话,可以用 阿贝尔恒等式 :

$$\large \sum_{i = 1}^{n} a_ib_i = b_n\sum_{i = 1}^{n} a_i + \sum_{i = 1}^{n - 1} a_i\left( \sum_{j = 1}^{i} a_j \right) (b_i - b_{i + 1})$$

方法 6#

无限微积分的算子 $D$ 可以理解为 $D \to 0$ ,那么考虑运用 差分算子 的有限积分.

首先,有限微积分基于 差分算子$\Delta$ :

$$\large \Delta f(x) = f(x + 1) - f(x)$$

为了更好的运用差分的性质,定义 上升幂 :

$$\large x^{\overline{n}} = x(x + 1)(x + 2) \cdots (x + n - 1)$$

定义 下降幂 :

$$\large x^{\underline{n}} = x(x - 1)(x - 2) \cdots (x - n + 1)$$

而且这个运算满足 :

$$\large \Delta(x^{\underline{n}}) = nx^{\underline{n - 1}}$$

也就是这是迎合差分的性质而创造的运算,当然我们在广义二项式里面也能看到它.

好的,现在让我们引入一个符号 :

$$\large f(x) \vert^{b}_{a} = f(b) - f(a)$$

那么对于有限微积分,有 :

$$\large \sum_{a}^{b} \Delta f(x) \delta x = \left. f(x) \right|_{a}^{b}$$

然后 :

$$\large x^{2} = x^{\underline{2}} + x^{\underline{1}}$$

于是对原来的和式做有限积分 :

$$\large\begin{aligned} \sum_{i = 1}^{n} i^2 &= \frac{n^{\underline{3}}}{3} + \frac{n^{\underline{2}}}{2}\\ &= \frac{n(n + 1)(2n + 1)}{6} \end{aligned}$$

方法 7#

考虑 生成函数 .

众所周知有一个求数列前缀和的技巧是在其生成函数前乘上 $(1 - x)^{-1}$,本质上就是和 $<1,1,1,1\cdots>$ 的 OGF 做卷积.

那么先写一个数列 $<n^2>$ 的生成函数 :

$$\large G(x) = \sum_{n = 0}^{\infty} n^2 x^n = \frac{x + x^2}{(1 - x) ^ 3}$$

那么

$$\large\begin{aligned} F(x) &= \frac{x + x^2}{(1 - x) ^ 4}\\ \end{aligned}$$

解一下 :

$$\large\begin{aligned} \sum_{i = 1}^{n} i^2 &= [x^n]\frac{x + x^2}{(1 - x) ^ 4}\\ &= [x^n](x(1 + x)\sum_{k}\binom{k + 3}{3}x ^ k)\\ &= \binom{n + 1}{3} + \binom{n + 2}{3}\\ &= \frac{n(n + 1)(2n + 1)}{6} \end{aligned}$$

方法 8#

涉及基础微分,极限,导数知识,但是预习了必修3就能看懂吧大概

首先怎么想到用微分呢?

我们写一个 $<1,1,1,\cdots>$ 的生成函数然后对其变形 :

$$\large G(x) = \sum_{n = 0}^{\infty} x^n = 1 + x + x^2 + \cdots$$

众所周知想要把一个因子 $n$ 放到生成函数的式子里就要对其做微分 :

然后考虑如何拼出来我们要求的平方和序列的生成函数 :

$$\large x^2 G(x)^{\prime\prime} + x G(x)^{\prime} = \sum_{n = 0}^{\infty} sq_n x^n$$

引入 (选修2就有的) 等比数列求和公式 :

$$\large \sum_{i = 0}^{n} x^i = 1 + x + x^2 + x^3 + \cdots + x^n = \frac{x^{n + 1} - 1}{x - 1}$$

对其进行两次微分,得到 :

$$\large\begin{aligned} &1^2 + 2^2 x + 3^2 x^2 + \cdots + n^2 x^{n - 1}\\ &= \frac{n^2x^{n + 2} - (2n^2 + 2n - 1)x^{n + 1} + (n + 1)^2 x^{n} - x - 1}{(x - 1)^3} \end{aligned}$$

两侧同乘 $x$ :

$$\large\begin{aligned} &1^2x + 2^2 x^2 + 3^2 x^3 + \cdots + n^2 x^{n}\\ &= \frac{n^2x^{n + 3} - (2n^2 + 2n - 1)x^{n + 2} + (n + 1)^2 x^{n + 1} - x^2 - x}{(x - 1)^3} \end{aligned}$$

可以发现,求出 $x = 1$ 这一特殊情况后,此式子化为我们所要求的平方和,但是出现了 $\frac{0}{0}$ 的特殊情况.

根据 (有些人天天念叨的) 洛必达法则 :

发现分子分母两个函数在点 $1$ 附近 去心邻域 都可导并且 对于$g(x) = (x - 1)^3$ , 有 $g'(x) = 3(x - 1)^2 \neq 0$. 于是可以对于分子分母分别求导,连用三次洛必达 :

$$\large\begin{aligned} &\sum_{i = 1}^{n} i^2 \\ &= \lim_{x \to 1} \frac{n^2x^{n + 3} - (2n^2 + 2n - 1)x^{n + 2} + (n + 1)^2 x^{n + 1} - x^2 - x}{(x - 1)^3}\\ & \xlongequal{L'H} \frac{n^2(n + 3)x^{n + 2} - (n + 2)(2n^2 + 2n - 1)x^{n + 1} +(n + 1)^3 x^n - 2x - 1 }{3(x - 1)^2} \\ & \xlongequal{L'H} \frac{n^2(n + 3)(n + 2)x^{n + 1} - (n + 2)(n + 1)(2n^2 + 2n - 1)x^{n} + n(n + 1)^3 x^{n - 1} - 2 }{6(x - 1)} \\ & \xlongequal{L'H} \frac{1}{6} (n^2(n + 3)(n + 2)(n + 1)x^{n} - n(n + 1)(n + 2)(2n^2 + 2n - 1)x^{n - 1} + (n - 1)n(n + 1)^3 x^{n - 2}) \\ & = \frac{1}{6} (n^2(n + 3)(n + 2)(n + 1) - n(n + 1)(n + 2)(2n^2 + 2n - 1) + (n - 1)n(n + 1)^3) \\ & = \frac{n(n + 1)(2n + 1)}{6}\\ \end{aligned}$$

奇技淫巧#

为什么把下列的内容称作奇技淫巧呢?

因为其 不可推广 或者 难以想到.

难以想到和难以理解是不同的,想到是在没有解这个问题的实际经历时找到做法,理解是对于一个做法懂得做的过程,但是可能你是在解出问题后再以上帝视角理解的.

#1#

构造性证明

构造性/非构造性证明都和开脑洞似的...

看看平方和数列英文名 : Square Pyramidal Numbers .

直译就是 "方形金字塔数"

是因为这些数是很多能堆在一起形成一个 $n$ 层金字塔的数的和.

金字塔啥样,下面这样 :

$$\large\begin{aligned} &1\\ &2\,2\\ &3\,3\,3\\ &4\,4\,4\,4\\ &\vdots\\ &n\,n\,n\,\cdots n \end{aligned}$$

考虑从中间对齐的话,这是一个等边三角形.

不想排版了,凑合看吧.

翻转一下 :

$$\large\begin{aligned} &n\\ &n\,n - 1\\ &n\,n - 1\,n - 2\\ &n\,n - 1\,n - 2\,n - 3\\ &\vdots\\ &n\,n - 1\,n - 2\,\cdots 1 \end{aligned}$$

再转一下 :

$$\large\begin{aligned} &n\\ &n - 1\,n\\ &n - 2\,n - 1\,n\\ &n - 3\,n - 2\,n - 1\,n\\ &\vdots\\ &1\,2\,3\,\cdots n \end{aligned}$$

然后把三个三角形加起来得到的就是 $3sq_n$ ,每个位置的和都是 $2n + 1$ ,每个三角形有 $\frac{n(n + 1)}{2}$ 个数,于是有 :

$$\large 3sq_n = \frac{n(n + 1)(2n + 1)}{2}$$

#2#

来自 Youtube 频道 Think Twice 的形象化证明 :

链接

想必正常人类的空间想象力不足以立即想出这种证明...

或者说我太菜了才想不出来...

#3#

阿尔哈曾公式

就是那个专业对口了.

公式原型 :

$$\large \sum_{i = 1}^{n} i^{k + 1} = (n + 1)\sum_{i = 1}^{n} i^k - \sum_{i = 1}^{n}\sum_{j = 1}^{i} j^k$$

分别代入 $k = 0$ 与 $k = 1$ 即可...

#4#

物理方法...

我物理拉跨,那就看看别人怎么证明的吧.

知乎@wonderwind

总结#

后来去翻知乎回答,发现有一位小学老师的回答都有补充裂项求和法了,小学就有有限微积分,小学生恐怖如斯...

越到后面的方法就有越多复杂的概念,但是求解也更快(大嘘),总之,用高级知识解决低级问题就是 降维打击.

但是 OI 中更多体现的是使用数学将求值的复杂度降低到期望范围内,例如有了 $\mathrm{O}(k^3 \log n)$ 的矩乘优化递推有些时候就没必要做生成函数求通项了.

暴力#

暴力真好啊(感慨).

首先大胆猜一个结论.

看平方数的通项 : $f_n = n^2$ , 是二次的.

通项是 $n$ 次,大胆猜测这个数列前缀和的通项是 $n + 1$ 次的一个多项式.

代几个值然后大力消元.