[未完成]OI 中的数值计算初探

目录#

牛顿迭代
拉格朗日乘子法
高斯消元法
拉格朗日插值
自适应辛普森法
蒙特卡洛方法
更多随机化算法
更多内容

前言#

别拿数学污染 OI.jpg

应该不会再有这种毒瘤题了……大概？

update : 写了不到一半的时候

越写越发现数值计算东西很多……最开始其实只打算写牛顿迭代和拉格朗日乘数的。~~惊天巨坑~~

牛顿迭代#

理论部分#

牛顿迭代通常用于求解一个函数的近似根，阿贝尔-鲁菲尼定理指出，五次及更高次的代数方程没有一般的代数解法，也就是没有求根公式这样的精确解的形式，只能考虑求近似解。

泰勒展开#

逐渐偏离题目(?)

如果你不想看这部分就跳到四级标题 “如果我不想看泰勒展开呢？”处。

(乐-太乐-泰勒展开.jpg) (此处应有肯尼迪表情包但是我没做)

我们仿造一个函数，比如就 $g(x) = e^x$ 。仿造的前提是描述这个函数，我们可以用导数来描述函数。

但是只有一个一阶导是很无力的，容易被一转攻势，基本没有多少信息，那么考虑求出 $n$ 阶的导数，如果有一个 $f(x)$ 与 $g(x)$ 的一阶到 $n$ 阶导全相同，那么可以认为这两个函数是足够相似的。

然后我们发现 $f(x) = e^x$ 这个函数可以一直导一直导导个不停（无歧义）。

然后我们用一个足够多次的也能一直导的多项式去仿造，就能求多次导。

f (x) = lim_{n \to \infty} \sum_{i = 0}^{n} \frac{f^{(n)} (x_{0})}{n!} (x - x_{0})^{i} + R_{n} (x)

$\large f(x) = \lim_{n \rightarrow \infty} \sum_{i = 0}^{n}\frac{f^{(n)}(x_0)}{n!} (x - x_0)^i + R_n(x)$

但是显然真的要计算是不可能算到 $\infty$ 的，但是后面的佩亚诺余项会越来越小到一个能接受的误差范围，也算是求得一个解了。

于是我们只要泰勒展开的第一项：

\begin{aligned} f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) \end{aligned}

$\large\begin{aligned} f(x) = f(x_0) + f'(x_0)(x - x_0) \end{aligned}$

然后我们要求函数零点：

\begin{aligned} f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) = 0 \\ f^{'} (x_{0}) (x - x_{0}) = - f (x_{0}) \\ x = x_{0} - \frac{f (x_{0})}{f^{'} (x_{0})} \end{aligned}

$\large\begin{aligned} &f(x) = f(x_0) + f'(x_0)(x - x_0) = 0\\ &f'(x_0)(x - x_0) = -f(x_0)\\ &x = x_0 - \frac{f(x_0)}{f'(x_0)} \end{aligned}$

如果只要泰勒展开第一项精度不够怎么办？

迭代，每次把上一次的解代入，可以逼近零点。

于是得到迭代公式：

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})}

$\large x_{n + 1} = x_n - \dfrac{f(x_n)}{f'(x_n)}$

如果我不想看泰勒展开呢？#

那我们看函数图像理解一下：

对于一个函数 $f(x)$ ，我们求出其导数 $f'(x)$ 。

生成一个初始解 $x_0$ ，每次求出一条过点 $(x_0,f(x_0))$ 的，函数 $y = f(x)$ 的切线，这条切线的斜率就是 $f'(x_0)$ ，与 $x$ 轴交点为 $x_0 - \dfrac{f(x_0)}{f'(x_0)}$ ，可以发现一直重复这个过程就是在接近这个函数与 $x$ 轴的交点。

于是牛顿迭代有迭代式如下：

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})}

$\large x_{n + 1} = x_n - \dfrac{f(x_n)}{f'(x_n)}$

何时不能牛顿迭代#

迭代初始值选到了驻点，使 $f'(x) = 0$
函数不收敛，越跑越远

多元函数牛顿迭代#

把导数改成梯度。

~~唐突线性代数~~

牛顿迭代具体过程#

首先我们需要 $f(x)$ 和 $f'(x)$ ，然后选择一个初始解，开始迭代即可。

牛顿迭代法具有平方收敛的性能，也就是说其为 $\mathcal{O} (\log n)$ 的。

例：求出 $\sqrt{x}$ ，首先 $\sqrt{a}$ 可以理解为方程 $x^2 - a = 0$ 的一个根，那么对原函数 $f(x) = x^2 - a$ 求导得到 $f'(x) = 2x$ ，然后直接迭代即可。

参考代码：

#include <cstdio>
#include <cmath>
#include <algorithm>
using std::abs;
constexpr double eps = 1e-9;

inline double NewtonSqrt(double x) {
	double x0 = x;
	while(abs(x0 * x0 - x) > eps)
		x0 -= (x0 * x0 - x) / (2 * x0);
	return x0;
}

int main() {
	double x;
	scanf("%lf",&x);
	printf("Newton's method %.8lf\n",NewtonSqrt(x));
	printf("std::sqrt %.8lf\n",std::sqrt(x));
	return 0;
}

可以发现迭代的初始值并不是非常重要，但是如果有一个较好的初始解，迭代次数会明显减少，著名的快速平方根倒数算法就是使用了 “魔法数字”
0x5f3759df 然后只进行一次迭代而大大加快了速度。

在 Chris Lomont 的论文中给出了一个效率略好于 Quake III 源代码的优秀初值 : 0x5f375a86。

论文链接 : http://www.lomont.org/papers/2003/InvSqrt.pdf

#include <cstdio>
#include <cmath>
#include <algorithm>
using std::abs;
constexpr double eps = 1e-9;

inline float NewtonSqrt(float x) {
   float halfx = 0.5 * x;
   int i = *((int *)&x);
   i = 0x5f3759df - (i>>1);
   x = *((float *)&i);
   x = x * (1.5 - (halfx * x * x));
   return 1.0 / x;
} 

int main() {
   double x;
   scanf("%lf",&x);
   printf("Fast Sqrt %.8lf\n",NewtonSqrt(x));
   printf("std::sqrt %.8lf\n",std::sqrt(x));
   return 0;
}

当然这个方法还有 double 版本，使用的初始解为 0x5fe6eb50c7aa19f9。

#include <cstdio>
#include <cmath>
#include <algorithm>
using std::abs;
constexpr double eps = 1e-9;

inline double NewtonSqrt(double x) {
    double halfx = 0.5 * x;
    long long i = *((long long *)&x);
    i = 0x5fe6eb50c7aa19f9 - (i >> 1);
    x = *((double *)&i);
    x = x * (1.5 - (halfx * x * x));
    return 1.0 / x;
} 

int main() {
	double x;
	scanf("%lf",&x);
	printf("Fast Sqrt %.8lf\n",NewtonSqrt(x));
	printf("std::sqrt %.8lf\n",std::sqrt(x));
	return 0;
}

不过这个平方根倒数效率已经被 SSE 指令集的 rsqrtss 吊打了 ~~硬件的胜利就是冯·诺依曼的胜利！~~。

例题#

平衡点#

$\texttt{Link.}$

求平面上的带权费马点。

这个问题似乎叫 费马-韦伯问题（？），我不确定，不敢乱说。

首先我们先不带权看一看，也就是普通的费马问题：

对于 $n = 3$ 也就是三角形费马点，数学家、物理学家托里拆利给出了一个平面几何的优秀解法：

当三角形的三个角均小于 $120°$ 时，所求的点为三角形的正等角中心。
当三角形有一内角大于或等于 $120°$ 时，所求点为三角形最大内角的顶点。

但是对于 $n$ 更大的问题，就没有一个更好的解法了。

现在我们具体考虑问题求的是什么：

对于 $n$ 个 $(x_i,y_i)$ ，求一个 $(x,y)$ 使得

\sum_{i = 1}^{n} \sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}

$\large \sum_{i = 1}^{n} \sqrt{(x - x_i)^2 + (y - y_i)^2}$

的值最小化。

（带权费马点就是求 $\sum_{i = 1}^{n} w_i\sqrt{(x - x_i)^2 + (y - y_i)^2}$ ）

于是现在问题转化为求一个二元函数极值：

min f (x, y) = \sum_{i = 1}^{n} \sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}

$\large \min f(x,y) = \sum_{i = 1}^{n} \sqrt{(x - x_i)^2 + (y - y_i)^2}$

首先为了得到这个函数的变化率和凹凸性，我们需要对其求导，但是对于一个二元函数，我们需要固定一个自变量不变，然后求另一个自变量变化与因变量的关系，相当于求了两个一元函数的导数，这时候两个导数为这个二元函数的 偏导数。

求其偏导数得：

\begin{aligned} f_{x} (x, y) = \sum_{i = 1}^{n} \frac{x - x_{i}}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}} \\ f_{y} (x, y) = \sum_{i = 1}^{n} \frac{y - y_{i}}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}} \end{aligned}

$\large\begin{aligned} &f_x(x,y) = \sum_{i = 1}^{n} \frac{x - x_i}{\sqrt{(x - x_i)^2 + (y - y_i)^2}} \\ &f_y(x,y) = \sum_{i = 1}^{n} \frac{y - y_i}{\sqrt{(x - x_i)^2 + (y - y_i)^2}} \end{aligned}$

可知当 $f_x(x,y) = 0$ 且 $f_y(x,y) = 0$ 时得到这个函数的驻点。

然后我们求出二阶导：

\begin{aligned} \frac{\partial^{2} z}{\partial x^{2}} = \sum_{i = 1}^{n} \frac{(y - y_{i})^{2}}{{(\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}})}^{3}} \\ \frac{\partial^{2} z}{\partial y^{2}} = \sum_{i = 1}^{n} \frac{(x - x_{i})^{2}}{{(\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}})}^{3}} \end{aligned}

$\large\begin{aligned} &\frac{\partial^2 z}{\partial x^2} = \sum_{i = 1}^{n} \frac{(y - y_i)^2}{\left(\sqrt{(x - x_i)^2 + (y - y_i)^2} \right)^3}\\ &\frac{\partial^2 z}{\partial y^2} = \sum_{i = 1}^{n} \frac{(x - x_i)^2}{\left(\sqrt{(x - x_i)^2 + (y - y_i)^2} \right)^3} \end{aligned}$

可以看出这个二阶偏导数是恒大于 $0$ 的，于是这个函数是凸函数。

（所以我们可以直接分别三分 $x,y$ 就解出了此题，非常的合理啊）

原函数是个凸函数，于是一阶偏导数为 $0$ 的点就是它的最小值点，考虑如何求解如下方程：

\begin{aligned} \sum_{i = 1}^{n} \frac{x - x_{i}}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}} = 0 \\ \sum_{i = 1}^{n} \frac{y - y_{i}}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}} = 0 \end{aligned}

$\large\begin{aligned} &\sum_{i = 1}^{n} \frac{x - x_i}{\sqrt{(x - x_i)^2 + (y - y_i)^2}} = 0 \\ &\sum_{i = 1}^{n} \frac{y - y_i}{\sqrt{(x - x_i)^2 + (y - y_i)^2}} = 0 \end{aligned}$

使用牛顿迭代求解：

表示 $x$ 与 $y$ 如下：

\begin{aligned} x = \frac{\sum_{i = 1}^{n} \frac{x_{i}}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}}}{\sum_{i = 1}^{n} \frac{1}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}}} \\ y = \frac{\sum_{i = 1}^{n} \frac{x_{i}}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}}}{\sum_{i = 1}^{n} \frac{1}{\sqrt{(x - x_{i})^{2} + (y - y_{i})^{2}}}} \end{aligned}

$\Large\begin{aligned} x = \frac{\sum_{i = 1}^{n} \frac{x_i}{\sqrt{(x - x_i)^2 + (y - y_i)^2}} } {\sum_{i = 1}^{n} \frac{1}{\sqrt{(x - x_i)^2 + (y - y_i)^2}}}\\ y = \frac{\sum_{i = 1}^{n} \frac{x_i}{\sqrt{(x - x_i)^2 + (y - y_i)^2}} } {\sum_{i = 1}^{n} \frac{1}{\sqrt{(x - x_i)^2 + (y - y_i)^2}}} \end{aligned}$

然后大力迭代即可，带权就再乘一下。

如何更快求解？将初始解设为质心：

\begin{aligned} x_{0} = \frac{\sum_{i = 1}^{n} w_{i} x_{i}}{n} \\ y_{0} = \frac{\sum_{i = 1}^{n} w_{i} y_{i}}{n} \end{aligned}

$\large\begin{aligned} x_0 = \frac{\sum_{i = 1}^{n}w_ix_i}{n}\\ y_0 = \frac{\sum_{i = 1}^{n}w_iy_i}{n} \end{aligned}$

然后记得特判掉只有一个点的情况。

跑得飞快，能进最优解第一页。

// Fermat Point

#define sq(x) ((x) * (x))
std::pair<db,db> p[N];
db w[N];

int main() {
    InitIO();
	int n = read();
	db x0 = 0,y0 = 0;
	rep(i,1,n) {
		p[i].first = readDB();
		p[i].second = readDB();
		w[i] = read();
		x0 += p[i].first * w[i];
		y0 += p[i].second * w[i];
	}
	x0 /= n,y0 /= n;
	if(n != 1) {
    	while(1) {
    		db x1 = 0,x2 = 0,y1 = 0,y2 = 0;
    		rep(i,1,n) {
    			db g = std::sqrt(sq(x0 - p[i].first) + sq(y0 - p[i].second)) / w[i];
    			// You can use your Newton's Method Square Root instead OuO
    			x1 += p[i].first / g;
    			x2 += 1 / g;
    			y1 += p[i].second / g;
    			y2 += 1 / g;
    		}
    		x1 /= x2,y1 /= y2;
    		if(std::abs(x1 - x0) < eps && std::abs(y1 - y0) < eps)
    			break;
    		else x0 = x1,y0 = y1;
    	}
    	writeDB(x0,3),space;
		writeDB(y0,3),enter;
	}
	else {
		writeDB(p[1].first,3),space;
		writeDB(p[1].second,3),enter;
	}
    EndIO();
    return 0;
}

然后这个题还可以用其他数值计算的方法求解，例如 @damocris 大佬写的 Broydent 迭代：https://www.luogu.com.cn/record/67174683

一元三次方程求解#

$\texttt{Link.}$

(真的有人这个题不是用三分吗)

多项式求导：

$\dfrac{x}{\mathrm{d}x} x^k = kx^{k - 1}$

对于本题，对象函数为 $f(x) = ax^3 +bx^2 +cx + d$

导数为 $f'(x) = 3ax^2 + 2bx + c$

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <set>

typedef double db;
constexpr db eps = 1e-3;

db a,b,c,d;
inline db f(db x) {
	return a * x * x * x + b * x * x + c * x + d;
}

inline db fder(db x) {
	return 3.0 * a * x * x + 2.0 * b * x + c;
}

struct Node {
	db val;
	Node(){}
	Node(db v) :val(v) {}
	inline bool operator == (const Node &oth) const {
		return std::abs(val - oth.val) < eps;
	}
	inline bool operator < (const Node &oth) const {
		return -(val - oth.val) > eps;
	}
};
std::set<Node> res;

int main() {
	scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
	for(int i = -100;i <= 100;++i) {
		db x0 = i;
		while(std::abs(f(x0)) > eps)
			x0 -= f(x0) / fder(x0);
		res.emplace(x0);
	}
	for(auto i : res)
		printf("%.2lf ",i.val);
	return 0;
}

甚至可以实现一个简（huan）单（man）的高次方程求解：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <set>

typedef double db;
constexpr db eps = 1e-3;
constexpr int N = 105;

int n;
db a[N];
db d[N];
inline db f(db x) {
	db res = 0,rx = 1;
	for(int i = 0;i <= n;++i) {
		res += rx * a[i];
		rx *= x;
	}
	return res;
}

inline db fder(db x) {
	db res = 0,rx = 1;
	for(int i = 0;i < n;++i) {
		res += rx * a[i];
		rx *= x;
	}
	return res;
}

struct Node {
	db val;
	Node(){}
	Node(db v) :val(v) {}
	inline bool operator < (const Node &oth) const {
		return -(val - oth.val) > eps;
	}
};
std::set<Node> res;

int main() {
	scanf("%d",&n);
	for(int i = n;~i;--i)
		scanf("%lf",&a[i]);
	for(int i = n;i;--i)
		d[i - 1] = a[i] * i;
	for(int i = -100;i <= 100;++i) {
		db x0 = i;
		while(std::abs(f(x0)) > eps)
			x0 -= f(x0) / fder(x0);
		res.emplace(x0);
	}
	for(auto i : res) if(std::isnormal(i.val))
		printf("%.2lf ",i.val);
	return 0;
}

牛顿迭代总结(?)#

能够求解一些函数零点问题或者把函数极值问题转化为导数零点来求其驻点，在多项式中同样应用广泛。

拉格朗日乘数法#

拉格朗日乘数法题好少啊……基本都是网上搜别人博客找的。

拉格朗日乘数法是一种在约束条件下求多元函数极值的方法。

理论部分#

首先是无约束条件下多元函数极值问题：

例如对于一个函数 $f(x,y)$ 求极值，列方程求出点 $(x_0,y_0)$ 使其每个偏导数都为 $0$ ，称为函数的驻点，在 $(x_0,y_0)$ 某邻域一阶及二阶偏导数存在时极值点是这个驻点。

极值的充分条件为：

点 $(x_0,y_0)$ 某邻域一阶及二阶偏导数存在，且有 $f_x(x_0,y_0) = 0,f_y(x_0,y_0) = 0$ ，令 $A = f_{xx}(x_0,y_0),B = f_{xy}(x_0,y_0),C = f_{yy}(x_0,y_0)$ ，则有：

$AC - B^2 > 0$ 时有极值， $A > 0$ 取极大值， $A < 0$ 取极小值。
$AC - B^2 < 0$ 时没有极值。
$AC - B^2 = 0$ 时无法确定。

例如求二元函数 $f(x,y)$ 在约束条件 $\varphi (x,y) = c$ 下的条件极值，首先引入拉格朗日乘子 $\lambda$ 构造辅助函数 $F(x,y,\lambda) = f(x,y) + \lambda (\varphi(x,y) - c)$ ，此时求辅助函数极值得到原函数极值。

对于多元函数 $F(x,y,\lambda)$ 求极值参考上面的做法即可。

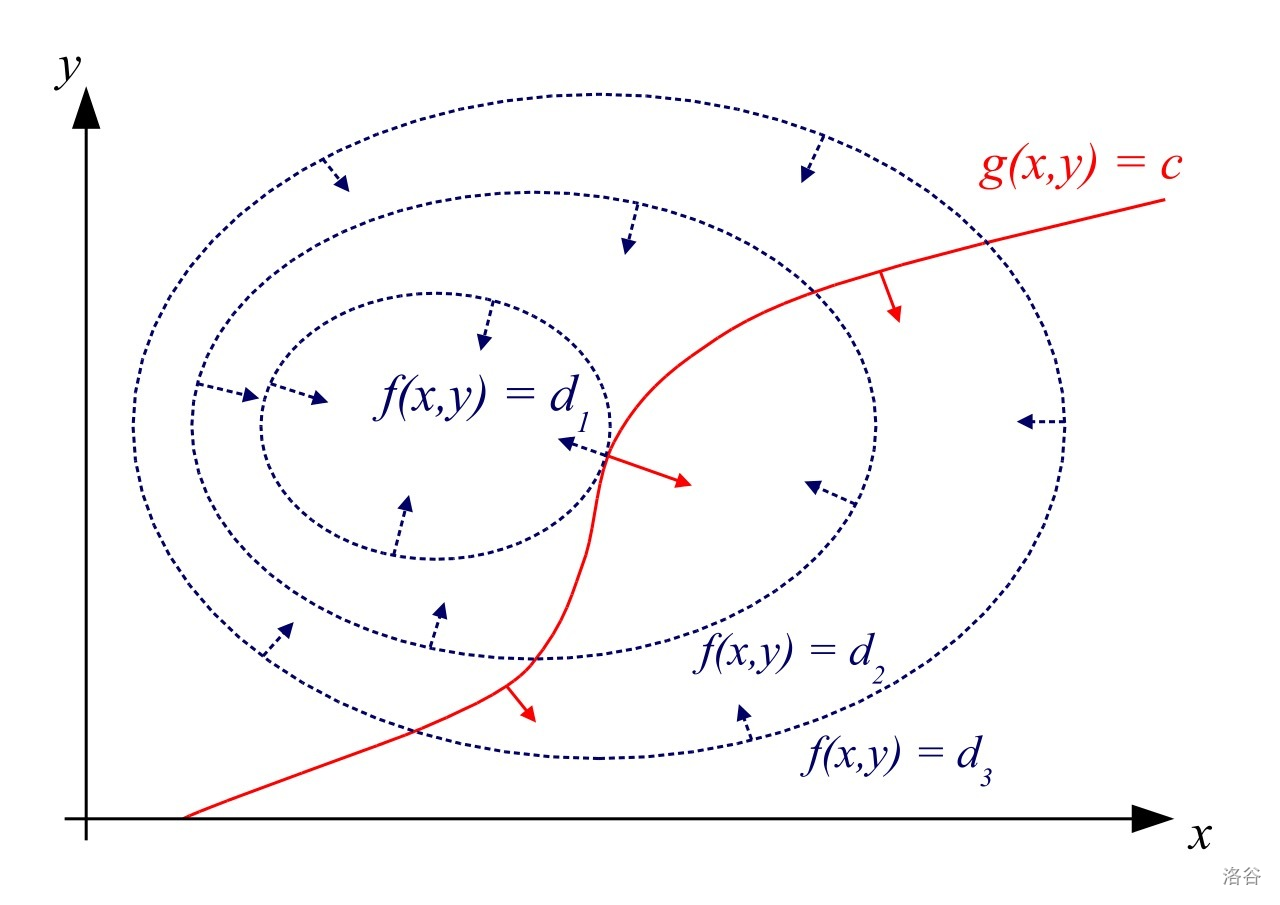
简要解释，下图蓝色为函数 $f(x,y)$ ，红色为约束条件 $g(x,y) = c$ 。

这时候找极值就相当于找一条最大的与 $g(x,y) = c$ 有交的等值线，可以发现最终找到的等值线与 $g(x,y) = c$ 相切，否则可以再调整得到更大的值。

此时两曲线有共线法向量，于是有以下等量关系：

\begin{aligned} \nabla f (x, y) = - λ \nabla g (x, y) \\ \nabla f (x, y) + λ \nabla g (x, y) = 0 \\ \nabla (f (x, y) + λ g (x, y)) = 0 \end{aligned}

$\large\begin{aligned} &\nabla f(x,y) = -\lambda \nabla g(x,y)\\ &\nabla f(x,y) + \lambda \nabla g(x,y) = 0\\ &\nabla (f(x,y) + \lambda g(x,y)) = 0 \end{aligned}$

然后列成方程的形式：

{\begin{matrix} f_{x} (x, y) + λ g_{x} (x, y) = 0 \\ f_{y} (x, y) + λ g_{y} (x, y) = 0 \\ g (x, y) = c \end{matrix}

$\large\left\{\begin{matrix} &f_x(x,y) + \lambda g_x(x,y) = 0\\ &f_y(x,y) + \lambda g_y(x,y) = 0\\ &g(x,y) = c \end{matrix}\right.$

例题#

yja#

来源网络。

二维平面上有 $n$ 个点，我们已知每个点 $i$ 距离原点的距离 $r_i$ 而不知具体位置，确定这些点的位置，求最大能构成的凸包面积，保证 $n \le 8$

$n$ 很小，全排列枚举构成凸包的点以及所选点的排列顺序，贪心地考虑，总是选最长的，不需要再 $2^i$ 枚举集合。

将每个 $r$ 视作起点为原点长度为 $r$ 的可以旋转的向量 $\vec r$ ，记 $\vec r_i 和 \vec r_{i \bmod n + 1}$ 夹角为 $\theta_i$ ，通过向量外积来表示面积：

S = \frac{1}{2} \sum_{i = 1}^{k} | {\vec{r}}_{i} | | {\vec{r}}_{i mod k + 1} | \sin (θ_{i})

$\large S = \frac{1}{2}\sum_{i = 1}^{k} |\vec r_i||\vec r_{i \bmod k + 1}|\sin(\theta_i)$

约束条件为：

\sum_{i = 1}^{k} θ_{i} = 2 π

$\large \sum_{i = 1}^{k} \theta_i = 2\pi$

构造辅助函数得：

F (θ_{1}, θ_{2}, \dots, θ_{k}, λ) = \frac{1}{2} \sum_{i = 1}^{k} | {\vec{r}}_{i} | | {\vec{r}}_{i mod k + 1} | \sin (θ_{i}) + λ (\sum_{i = 1}^{k} θ_{i} - 2 π)

$\large F(\theta_1,\theta_2,\cdots,\theta_k,\lambda) = \frac{1}{2}\sum_{i = 1}^{k} |\vec r_i||\vec r_{i \bmod k + 1}|\sin(\theta_i) + \lambda (\sum_{i = 1}^{k} \theta_i - 2\pi)$

然后求偏导得到：

| {\vec{r}}_{i} | | {\vec{r}}_{i mod k + 1} | \cos (θ_{i}) = λ

$\large |\vec r_i||\vec r_{i \bmod k + 1}|\cos(\theta_i) = \lambda$

即

θ_{i} = \arccos (\frac{λ}{| {\vec{r}}_{i} | | {\vec{r}}_{i mod k + 1} |})

$\large \theta_i = \arccos{\left(\frac{\lambda}{|\vec r_i||\vec r_{i \bmod k + 1}|}\right)}$

并且有 $\theta_i \in [0,\pi]$ ，这时候 $\lambda$ 具有单调性了，二分 $\lambda$ 然后检查 $\sum \theta$ 是否为 $2\pi$ 即可求出此种方案最大面积。

river#

$\texttt{Link.}$

一条南北向河流有 $n$ 段，从西到东流速分别为 $v_i$ ，宽度分别为 $w_i$ ，游泳速度为 $u$ 现在要在 $T$ 秒内从西岸游到东岸，求南北方向最大的位移。

对于每个河段，如果分配的时间一定，我们可以求出恰好使用 $t$ 时间的最大南北向位移记作一个函数 $f_i(t) = v_i t + \sqrt{u^2 t^2 - w_i^2}$

这时有约束： $\sum_{i = 1}^{n} t_i = T$ ，最大化 $\sum f_i(t_i)$

求出偏导数：

f_{i}^{'} (t) = \frac{u^{2} t}{\sqrt{u^{2} t^{2} - w_{i}^{2}}} + v_{i}

$\large f_i'(t) = \frac{u^2 t}{\sqrt{u^2 t ^2 - w_i^2}} + v_i$

通过拉格朗日乘数可知此时导函数值相同，可以二分函数值然后反代求总时长，对于一个函数值 $x$ ，有：

x = \frac{u^{2} t}{\sqrt{u^{2} t^{2} - w_{i}^{2}}} + v_{i} x \sqrt{u^{2} t^{2} - w_{i}^{2}} = u^{2} t + v \sqrt{u^{2} t^{2} - w_{i}^{2}} (x - v) \sqrt{u^{2} t^{2} - w_{i}^{2}} = u^{2} t (x^{2} - 2 v x + v^{2}) (u^{2} t^{2} - w_{i}^{2}) = u^{4} t^{2} u^{2} t^{2} (x^{2} - 2 v x + v^{2}) - w^{2} (x^{2} - 2 v x + v^{2}) = u^{4} t^{2} (u^{2} (x - v)^{2} - u^{4}) t^{2} = w^{2} (x - v)^{2} t^{2} = \frac{w^{2} (x - v)^{2}}{u^{2} (x - v)^{2} - u^{4}} t = \sqrt{\frac{w^{2} (x - v)^{2}}{u^{2} (x - v)^{2} - u^{4}}}

$\large x = \frac{u^2 t}{\sqrt{u^2 t ^2 - w_i^2}} + v_i\\ x\sqrt{u^2 t ^2 - w_i^2} = u^2 t + v\sqrt{u^2 t ^2 - w_i^2}\\ (x - v)\sqrt{u^2 t ^2 - w_i^2} = u^2 t\\ (x^2 - 2vx + v^2)(u^2 t ^2 - w_i^2) = u^4 t^2\\ u^2 t^2 (x^2 - 2vx + v^2) - w^2 (x^2 - 2vx + v^2) = u^4 t^2\\ (u^2 (x - v)^2 - u^4) t^2 = w^2 (x - v)^2\\ t^2 = \frac{w^2 (x - v)^2}{u^2 (x - v)^2 - u^4}\\ t = \sqrt{\frac{w^2 (x - v)^2}{u^2 (x - v)^2 - u^4}}$

于是可以以此计算每条河段的用时，最后依二分得到的用时计算 $\sum f_i$ 即可。

NOI2012 骑行川藏#

$\texttt{Link.}$

有 $n$ 个路段，每条路段有三个参数 $s_i,k_i,v'_i$ 分别为长度，风阻系数，风速。

对于第 $i$ 段路全程以 $v$ 的速度前进，代价为 $E_i(v) = k_is_i(v - v'_i)^2$

在 $\sum E$ 不超过 $E_U$ 的条件下最小化 $\sum \frac{s_i}{v_i}$ 。

表示成多元函数和约束条件的形式：

f (v_{1}, v_{2}, \dots, v_{n}) = \sum_{i = 1}^{n} \frac{s_{i}}{v_{i}} φ (v_{1}, v_{2}, \dots, v_{n}) = \sum_{i = 1}^{n} k_{i} s_{i} (v_{i} - v_{i}^{'})^{2} = E_{U}

$\large f(v_1,v_2,\cdots,v_n) = \sum_{i = 1}^{n} \frac{s_i}{v_i}\\ \varphi (v_1,v_2,\cdots,v_n) = \sum_{i = 1}^{n} k_i s_i (v_i - v'_i)^2 = E_U$

构造辅助函数得：

F (v_{1}, v_{2}, \dots, v_{n}, λ) = f (v_{1}, v_{2}, \dots, v_{n}) + λ (φ (v_{1}, v_{2}, \dots, v_{n}) - E_{U})

$\large F(v_1,v_2,\cdots,v_n,\lambda) = f(v_1,v_2,\cdots,v_n) + \lambda (\varphi (v_1,v_2,\cdots,v_n) - E_U)$

求偏导数：

2 λ k_{i} s_{i} (v_{i} - v_{i}^{'}) = - \frac{s_{i}}{v_{i}^{2}} (1) \sum_{i = 1}^{n} k_{i} s_{i} (v_{i} - v_{i}^{'})^{2} = E_{U}

$\large 2\lambda k_i s_i (v_i - v'_i) = -\frac{s_i}{v_i^2} (1)\\ \sum_{i = 1}^{n} k_i s_i (v_i - v'_i)^2 = E_U$

由 $(1)$ ：

2 λ k_{i} v_{i}^{2} (v_{i} - v_{i}^{'}) = - 1

$\large 2\lambda k_i v_i^2 (v_i - v'_i) = -1$

于是可知 $\lambda < 0$ ，移项得到：

v_{i}^{2} (v_{i} - v_{i}^{'}) = - \frac{1}{2 λ k_{i}}

$\large v_i^2(v_i - v'_i) = -\frac{1}{2 \lambda k_i}$

可以发现这是单调的，考虑二分 $\lambda$ 得到仅剩常数和 $v_i$ 的方程，三次方程求根即可。

高斯消元法#

拉格朗日插值#

这应该也算是数值计算（？）

自适应辛普森法#

蒙特卡洛方法#

Pollard-Rho 离散对数也是一种 Monte Carlo，优点是空间开销小于 BSGS 并且更快。

Loading...

AstatineAi

[未完成]OI 中的数值计算初探

目录#

前言#

牛顿迭代#

理论部分#

泰勒展开#

如果我不想看泰勒展开呢？#

何时不能牛顿迭代#

多元函数牛顿迭代#

牛顿迭代具体过程#

例题#

平衡点#

一元三次方程求解#

牛顿迭代总结(?)#

拉格朗日乘数法#

理论部分#

例题#

yja#

river#

NOI2012 骑行川藏#

高斯消元法#

拉格朗日插值#

自适应辛普森法#

蒙特卡洛方法#

更多随机化算法#

更多内容#

公告

搜索

常用链接

最新随笔

我的标签

随笔分类 (48)

随笔档案 (37)

阅读排行榜

评论排行榜

推荐排行榜

最新评论