最小割相关问题
CSP T4 的 60 分最小割都没看出来,气死我了.
什么是最小割
---以下是引用 神 \(\mathrm{{\color{black}w}{\color{red}{ind\_whisper}}}\) 的话---
所谓最小割,就是最小的割
(逃)
---以上是引用 神 \(\mathrm{{\color{black}w}{\color{red}{ind\_whisper}}}\) 的话---
通常我们考虑的都是 有源汇网络 的最小割.
对于一个网络,将其所有点划分为两个集合,一个集合含有源点,另一个集合含有汇点,这样一个划分方案被称为 割.
最小割就是一个使得断掉的边权值和最小的划分方案.
补充 : 无源汇最小割
一种使得整个网络恰好分为两个子图且最小化断边边权和的断边方案.
可以使用 Stoer-Wagner 算法在近似 \(\mathrm{O}(n^3)\) 时间内解决.
如何求最小割
最大流最小割定理
对于一个网络,其最小割 \(c(S,T)_{\min}\) 等于其 最大流 \(f(S,T)_{\max}\).
于是在这个定理加持下,可以使用 dinic 在 \(\mathrm{O}(n^2m)\) 时间内求出最小割.
但是正常来说显然是跑不满的,实在不行就HLPP吧
例题
只放出建图部分的代码,最小割直接把你的 dinic 接上去即可.
T1
求使得一棵带边权树的根和每个叶子都不连通的最小断边边权和.
因为写不出来树型DP就来直接考虑最小割.
显然是把根作为源点,叶子连接到超级汇点然后用边权作为流量,叶子向汇点的流量为无限大(即标记为不可割)即可.
代码不放了.
T2
P1345 [USACO5.4]奶牛的电信Telecowmunication
求使一无向图两点不连通的最小割点个数.
考虑如何把割边转化为割点.
拆点,把一个点转化为一个入点和一个出点,出入点之间用容量为1的边相连,对于原图的每一条边 \((s,t)\),转化为
\(s\) 的出点向 \(t\) 的入点连边, \(t\) 的出点向 \(s\) 的入点连边,容量均为无限大即可.
int n = read(),m = read();s = read(),t = read();
s += n;
rep(i,1,n)
AddEdge(i,i + n,1);
rep(i,1,m) {
int st = read(),ed = read();
AddEdge(st + n,ed,INF);
AddEdge(ed + n,st,INF);
}
T3
P2944 [USACO09MAR]Earthquake Damage 2 G
和上一题差不多,就是只有一部分点需要连汇点.
int n = read(),m = read(),p = read();s = 1 + n,t = (n << 1) + 1;
ff(i,1,m) {
int st = read(),ed = read();
AddEdge(st + n,ed,INF);
AddEdge(ed + n,st,INF);
}
ff(i,1,p) {
int st = read();
vis[st] = 1;
AddEdge(st + n,t,INF);
}
ff(i,1,n) if(!vis[i])
AddEdge(i,i + n,1);
else AddEdge(i,i + n,INF);
T4
P2057 [SHOI2007]善意的投票 / [JLOI2010]冠军调查
最小割经典模型之元素分成两个集合.
令源点代表一个集合,汇点代表另一个集合,对于每个冲突关系,在两人之间建一条正反容量均为1的边即可.
int n = read(),m = read();s = 0,t = n + 1;
ff(i,1,n) {
int flag = read();
if(flag) AddEdge(s,i,1);
else AddEdge(i,t,1);
}
ff(i,1,m) {
int st = read(),ed = read();
AddEdge(st,ed,1),AddEdge(ed,st,1);
}
T5
一个物品分到两个集合分别有不同的价值 -> 源点代表集合 B ,向该点连分入集合 A 的价值,汇点代表集合 B ,该点连到汇点分入集合 A 的价值.
考虑如何实现数个作物在同一集合能获得一定价值.
割和源点连的边就代表分入汇点所在的集合,那么只要两个点在同一集合(即同时和源点或者汇点连通)时,建立一条不需要被割掉的边即可.
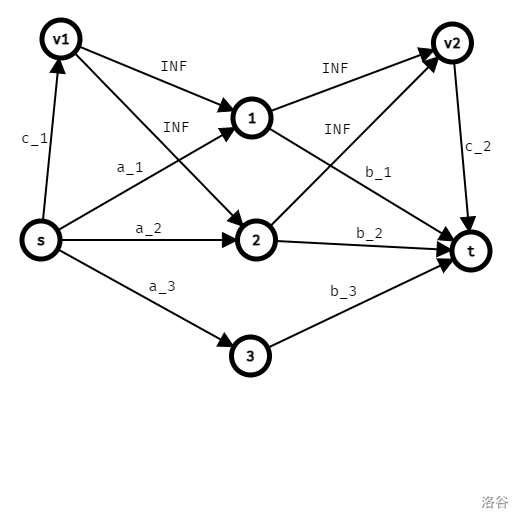
建立两个虚拟节点,一个代表同时连接源点能获得的价值,也就是从源点向虚拟节点连接容量为 \(c\) 的边,虚拟节点向有关系的多个作物连无限容量的边.
另一个同理,向汇点连边.
如图 :
ll sum = 0;
ff(i,1,n) {
ll w = read();
AddEdge(s,i,w);
sum += w;
}
ff(i,1,n) {
ll w = read();
AddEdge(i,t,w);
sum += w;
}
int m = read();
ff(i,1,m) {
int cnt = read();
ll w1 = read(),w2 = read();
AddEdge(s,i * 2 - 1 + n,w1);
AddEdge(i * 2 + n,t,w2);
ff(j,1,cnt) {
int p = read();
AddEdge(i * 2 - 1 + n,p,1000000000);
AddEdge(p,i * 2 + n,1000000000);
}
sum += w1,sum += w2;
}
write(sum - dinic());
最后输出总价值减去最小失去的价值.
T6
把上一题的技巧用于网格,依然是源汇点代表两个集合,每个关系建立虚拟结点即可.
T7
从上一题的相邻相同有收益变成了相邻不同有收益,显然不能直接用源汇点代表两个集合.
考虑直接黑白染色.
源点向黑点连容量为 \(A_{i,j}\) 的边,向白点连容量为 \(B_{i,j}\) 的边.
黑点向汇点连容量为 \(B_{i,j}\) 的边,白点向汇点连容量为 \(A_{i,j}\) 的边.
然后黑白点之间连接容量为 \(C_{i,j} + C_{i \pm 1,j \pm 1}\) 的边即可.
这样使得相邻两个点都与源/汇点联通时(即分入不同的集合),可以不断开连接这两个点的边.
inline void AddEdge(int st,int ed,int cap,int c2 = 0) {
e[++ecnt] = (Edge) {head[st],ed,cap},head[st] = ecnt;
e[++ecnt] = (Edge) {head[ed],st,c2},head[ed] = ecnt;
}
#define Node(x,y) ((x - 1) * m + y)
int mian() {
init_IO();
mems(head,-1);
ll sum = 0;
int n = read(),m = read();s = 0,t = n * m + 1;
ff(i,1,n) ff(j,1,m) {
int a = read();sum += a;
if((i + j) & 1) AddEdge(s,Node(i,j),a);
else AddEdge(Node(i,j),t,a);
}
ff(i,1,n) ff(j,1,m) {
int b = read();sum += b;
if(!((i + j) & 1)) AddEdge(s,Node(i,j),b);
else AddEdge(Node(i,j),t,b);
}
ff(i,1,n) ff(j,1,m) {
int c = read();
if(i > 1) AddEdge(Node(i,j),Node(i - 1,j),c,c),sum += c;
if(i < n) AddEdge(Node(i,j),Node(i + 1,j),c,c),sum += c;
if(j > 1) AddEdge(Node(i,j),Node(i,j - 1),c,c),sum += c;
if(j < m) AddEdge(Node(i,j),Node(i,j + 1),c,c),sum += c;
}
write(sum - dinic());
end_IO();
return 0;
}
T8
P1344 [USACO4.4]追查坏牛奶Pollutant Control
除了求最小割还要求割边数量.
一种方式是在残量网络上更改边权后再求最大流,但是这道题的容量都很小.
考虑将每条边的容量乘一个足够大的质数后加一,那么最小割就是 这个新图的最小割除以那个质数,割边数就是新图的最小割模那个质数.
T9
乍一看就是最小割,但是其实出题人卡了朴素 Dinic .
但是这个问题的图没有类似前面的虚拟节点,是一个 平面图.
对于一个平面图,其最小割可以转化为对偶图上的最短路.
对于原图的每一个闭合区域,视作一个结点,把左下作为起点,右上作为终点,做一条从原来的源点到原来的汇点的对角线把原图外界区域分割成两部分.
如果有两个闭合区域有公共边,那么就在这两个点之间连边.
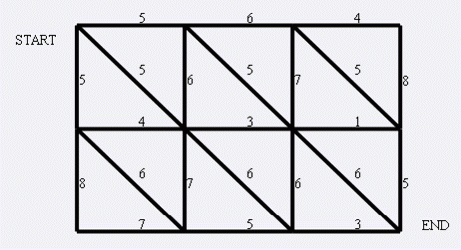
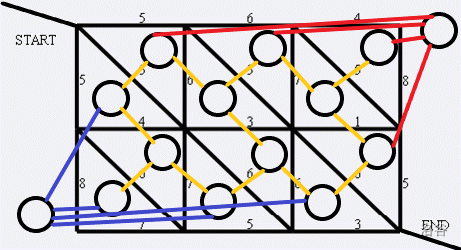
这样就是\(\mathrm{O} (n^2 \log n^2)\) 的复杂度了,可以通过本题.
T10
如何得60分.
相邻两端不同就要付出代价,直接最小割.
再加上出题人给了美好的 3s 时间限制,这种稠密图上 dinic 就可以得 60 分了.
可以看到就是最慢的一个点也只是600多毫秒.
如何得 80 分.
观察测试点范围,有对于测试点13 ~ 16,k = 2.
于是套用一下上面的狼抓兔子那道题,尝试做一个对偶图的最短路就可以了.
(然后你就可以只靠着T4得到省一等奖,写个1.5小时然后摆烂2.5小时)
如何得满分.
考虑 HLPP update 2022.1.26 : HLPP 没用
考虑 \(\mathrm{O}(VE)\) 的James B Orlin's + KRT (King, Rao, Tarjan)算法
考虑摆烂
考虑继续从最短路来扩展.
显然建了超级源点之后这个图就不是一个平面图了,不具有能建立对偶图后跑最短路的优秀性质.
update : 2022.1.26
下辈子保证补上!

