[学习笔记]二分图最大权匹配的 KM 算法

前言#

学这个的起因是 :

我的 OI-templates 需要二分图最大权匹配的板子但是我的 Primal-Dual 费用流无法通过洛谷的模板题.

一般图匹配可能这辈子都不会学了.

二分图最大权匹配#

一个二分图,边有边权,选出一定的边使得选出的边端点无交集.

最大化被选出的边的边权.

首先想一个比较 $naive$ 但是通常不会被卡的做法,参考最大流求二分图最大匹配 :

每个点可以给出最多 1 的贡献,但是带权.

那么先照例建出源点和汇点,源点连每个左边点 $<1,0>$ ,每个匹配从左连右 $<1,w>$ ,右侧连汇点 $<1,0>$ .

然后跑最大费用最大流.

但是可以发现如果有负权会导致为了最大化流量而选了负权边的问题,那就加边的时候把负权都变 $0$ 即可.

然后来做版子题 : $\texttt{Link.}$

这个题要求完美匹配,也就是能连边必须连,那就不能把负权变 $0$ 权了,欢乐写完,直接提交.

然后我就像前言说的那样,被卡了.

费用流最高似乎能拿个 40 分吧,但是我最高只有 37.

于是考虑~~更专业的~~更好的求二分图最大权匹配的算法.

KM 算法#

在 $\mathcal{O} (n^3)$ 时间内求出二分图的 最大权完美匹配.

如果二分图没法完美匹配其实加几个虚拟点然后匹配得到权值为 $0$ 即可.

然后是 KM 的几个约定.

可行顶表 : 对于结点 $u$ 有一个权值 $l(u)$ ,使得存在的边 $(u,v)$ 有 $w(u,v) \le l(u) + l(v)$ .

相等子图 : 包含原图所有点,但只有 $w(u,v) = l(u) + l(v)$ 的边的子图.

交错路 : 交错路始于非匹配点且由匹配边与非匹配边交错而成.

增广路 : 增广路是始于非匹配点且终于非匹配点的交错路.

交错树 : 增广路形成的树.

然后有定理如下 :

对于某组可行顶标,如果其相等子图存在完美匹配,那么,该匹配就是原二分图的最大权完美匹配.

于是求匹配的过程转化为调整顶标最大化匹配.

然后是 KM 的具体流程 :

初始化顶标#

令最初左侧结点可以任意和右侧结点连通,那么讲左侧结点顶标初始化为 $l(u) = \max \{w(u,v)\}$ .

右侧结点为 $l(u) = 0$ .

可以发现是一个左侧过大右侧过小的情形.

然后使用匈牙利算法增广,如果没能得到完美匹配,那么就需要一个调整顶标的过程.

这时 能走的增广路都走尽了.

比如下面这个从 OI-wiki 上找的图 :

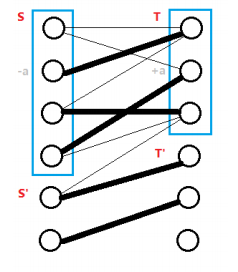
将匹配点涂上蓝色,然后从非匹配点向外画出增广路~~发现确实是一棵树,交错树成不我欺!~~.

然后这个图把所有点分成了四个点集, $S,S',T,T'$ .

分别代表 :

左点集交错树结点 $S$
左点集非交错树结点 $S'$
右点集交错树结点 $T$
右点集非交错树结点 $T'$

$S$ 到 $T'$ 的边不存在,否则交错树会连接到那个点.

$S'$ 到 $T$ 的边必定是非匹配边,同理上一条.

然后是调整顶标的过程,这里调整的显然是 $S,T$ ,来使得图产生匹配.

假设我们将 $S$ 中所有顶标减去 $a$ , $T$ 中所有顶标加上 $a$ .

对于现在图中的四类边分析 :

$S - T$ 边 : 正负相抵,依然满足 $l(u) + l(v) + w(u,v)$
$S' - T'$ 边 : 不受影响.
$S - T'$ 边 : $l(u) + l(v)$ 减小 $a$ ,使得一些边权更小的边可能产生匹配.
$S' - T$ 边 : $l(u) + l(v)$ 增大,已经超过可以产生新匹配的边权最大值,不影响.

于是需要在 $S - T'$ 边中取较小的作为 $a$ .

$a = \min \{l(u) +l(v) - w(u,v)\ | u \in S,v \in T'\}$

将一条边 $(u,v)$ 加入了相等子图后,如果 $v$ 不是匹配点,那么就可以在增广路继续增广.

然后这是一个 $\mathcal{O} (n^4)$ 的算法,因为找最小 $a$ 需要 $\mathcal{O} (n^2)$ .

显然在匹配这部分没啥可优化的了,于是考虑如何快速求出 $a$ .

考虑维护点集 $T$ 中点的一些信息,对于 $T$ 中每个点,维护 :

$\min\{l(u) + l(v) - w(u,v)\ | u \in S\}$

那么更新和修改就是 $\mathcal{O} (n)$ 的了.

模板 : $\texttt{Link.}$

模板要求求完美匹配,也就是不存在的边边权需要设为 $-\infty$ .

Code :

int n,m;

int match[N];
ll slack[N],lx[N],ly[N];
ll mp[N][N];
int pre[N];
bool visx[N],visy[N];

void argument(int u) {
	memset(slack,63,sizeof(ll) * (n + 1));
	memset(pre,0,sizeof(int) * (n + 1));
	match[0] = u;int x,y = 0,tmpy = 0;ll a;
	while(1) {
		x = match[y];a = INF;visy[y] = 1;
		rep(i,1,n) {
			if(visy[i]) continue;
			if(slack[i] > lx[x] + ly[i] - mp[x][i]) {
				slack[i] = lx[x] + ly[i] - mp[x][i];
				pre[i] = y;
			}
			if(slack[i] < a) {
				a = slack[i];
				tmpy = i;
			}
		}
		rep(i,0,n) if(visy[i])
			lx[match[i]] -= a,ly[i] += a;
		else
			slack[i] -= a;
		y = tmpy;
		if(match[y] == -1) break;
	}
	while(y) {
		match[y] = match[pre[y]];
		y = pre[y];
	}
}

ll KM() {
	memset(match,-1,sizeof(int) * (n + 1));
	memset(ly,0,sizeof(ll) * (n + 1));
	memset(lx,0,sizeof(ll) * (n + 1));
	rep(i,1,n) {
		memset(visy,0,sizeof(bool) * (n + 1));
		argument(i);
	}
	ll res = 0;
	rep(i,1,n) if(~match[i])
		res += mp[match[i]][i];
	return res;
}