张量(tensor)的广播
在使用numpy 对张量(数组)进行操作时,两个形状相同的张量进行加减等运算很容易理解,那么不同形状的张量之间的运算是通过广播来实现的。广播实际上很简单,但是弄清楚是也花了不小功夫,这里记录一下。
广播的目的是将两个不同形状的张量 变成两个形状相同的张量,即先对小的张量添加轴(使其ndim与较大的张量相同),在把较小的张量沿着新轴重复(使其shape与较大的相同)
广播的的限制条件为:两个张量的 trailing dimension(从后往前算起的维度)的轴长相等 或 其中一个的长度为1
import numpy as np a=np.arange(0,12) a=a.reshape(3,4) b=np.arange(0,4) print(a) #[[ 0 1 2 3] # [ 4 5 6 7] # [ 8 9 10 11]] print(b) #[0 1 2 3] print(a.shape) #(3, 4) print(b.shape) #(4,) print(a.ndim) #2 print(b.ndim) #1 a+b #array([[ 0, 2, 4, 6], # [ 4, 6, 8, 10], # [ 8, 10, 12, 14]])
上述 a+b 的计算过程等价为:
(1)先将b添加一个轴 即
(2)在将b沿着 新加的轴进行重复
b.reshape(1,4) #array([[0, 1, 2, 3]]) c=np.array([b,b,b]) #array([[0, 1, 2, 3], # [0, 1, 2, 3], # [0, 1, 2, 3]]) a+c #array([[ 0, 2, 4, 6], # [ 4, 6, 8, 10], # [ 8, 10, 12, 14]])
其他几个例子
x=np.arange(0,12) x=x.reshape(3,4,1) x y=np.arange(0,8) y=y.reshape(4,2) y q=x+y q.shape #(3,4,2)
x=np.arange(0,12) x=x.reshape(3,4,1) x z=np.arange(0,2) z=z.reshape(1,2) z q=x+z q.shape #(3,4,2)
x :  y
y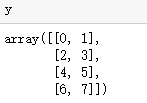 z
z 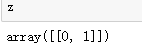 x+y
x+y  x+z
x+z 
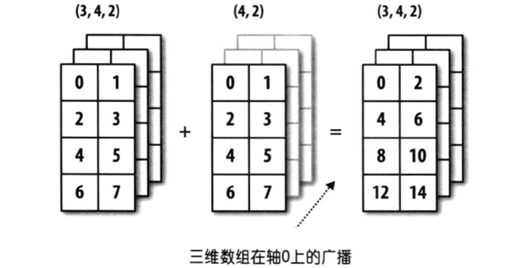
最后放上几个图片便于理解




 浙公网安备 33010602011771号
浙公网安备 33010602011771号