数据的存储(2):整数
前言
计算机中整数的使用可分为两种方式:一种只能表示非负数,称为无符号整型数;另一种能够表示负数、0以及正数,称为有符号整型数。本文简单说明整数在计算机中的存储形式。
无符号数的存储
对于无符号整数,数据在计算机中的表示就是普通的二进制数。通常,如果一个n位二进制数字序列
a
n
−
1
a
n
−
2
.
.
.
a
1
a
0
a_{n-1}a_{n-2}...a_1a_0
an−1an−2...a1a0表示一个无符号整数A,那么A的值则为:
A
=
∑
i
=
0
n
−
1
2
i
a
i
A = \sum_{i=0}^{n-1}2^ia_i
A=i=0∑n−12iai
以8位的二进制数字00101001为例,转换成10进制的值为41。对于一个n位的二进制无符号数,在计算机中能容纳的范围为
0
~
2
n
−
1
0~2^n-1
0~2n−1。
有符号数的存储
有符号数由于包含符号位,需要使用额外的bit位来表示符号信息,在大多数机器上,几乎都是使用补码来表示有符号整数。补码表示法中使用数据的最高有效位作为符号位,用以判断一个整数的正负性,非负数符号位为0,负数符号位为1。对于正数、0以及负数,根据其数值求取补码的规则如下:
- 正数的补码是其二进制表示,等于原码;
- 0的补码表示仍为0,并具有唯一性;
- 非负数的补码的计算方法是将非负数对应正数的原码除符号位外的所有位取反后加1。
使用位加权取和定义补码
补码的求取规则简单但是不方便理解,一个更好地说明补码的方式,是使用位加权取和的方式来定义补码。同无符号整型数,使用一个n位二进制数字序列
a
n
−
1
a
n
−
2
.
.
.
a
1
a
0
a_{n-1}a_{n-2}...a_1a_0
an−1an−2...a1a0表示一个有符号整数A,那么A的值则为:
A
=
−
2
n
−
1
a
n
−
1
+
∑
i
=
0
n
−
2
2
i
a
i
A = -2^{n-1}a_{n-1} + \sum_{i=0}^{n-2}2^ia_i
A=−2n−1an−1+i=0∑n−22iai
- 在A为正整数的情况下,符号位为0(即
a
n
−
1
a_{n-1}
an−1为0),故
−
2
n
−
1
a
n
−
1
-2^{n-1}a_{n-1}
−2n−1an−1为0,其余位按对应的权取值。该表达式定义了一个非负整数,可容纳的整数范围为
0
~
2
n
−
1
0~2^{n-1}
0~2n−1。以4位二进制整数0101为例,使用2的补码表示如下:
( 0101 ) 2 = − 0 ∗ 2 3 + 1 ∗ 2 2 + 0 ∗ 2 1 + 1 ∗ 2 0 = ( 5 ) 10 (0101)_{2} = -0 * 2^3 + 1* 2^2 + 0 * 2^1 + 1 * 2^0 =(5)_{10} (0101)2=−0∗23+1∗22+0∗21+1∗20=(5)10 - 在A为负整数的情况下,符号位为1(即
a
n
−
1
a_{n-1}
an−1为0),故
−
2
n
−
1
a
n
−
1
-2^{n-1}a_{n-1}
−2n−1an−1为
−
2
n
−
1
-2^{n-1}
−2n−1,其余位按对应的权取值,该表达式可以表示的所有负整数的范围为-1到
−
2
n
−
1
-2^{n-1}
−2n−1。以4位二进制整数1011威力,使用2的补码表示如下:
( 1011 ) 2 = − 1 ∗ 2 3 + 0 ∗ 2 2 + 1 ∗ 2 1 + 1 ∗ 2 0 = ( − 5 ) 10 (1011)_{2} = -1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 =(-5)_{10} (1011)2=−1∗23+0∗22+1∗21+1∗20=(−5)10
补码原理
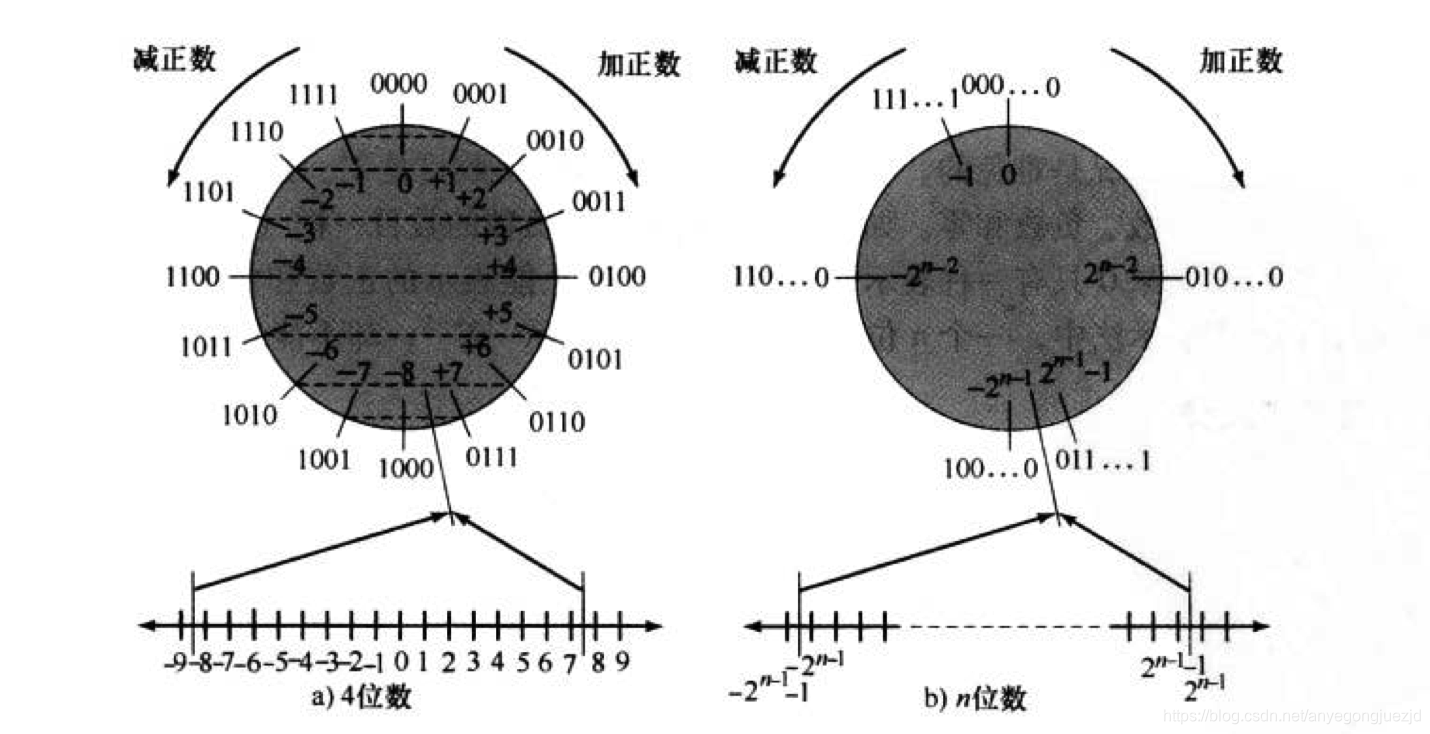
为了说明补码的原理,在此需要先引入“模”的概念:“模”是指一个计量系统的计数范围。计算机本身就一个计量系统,以4位整型数为例,参考下图,它能表示的范围是
0
~
2
4
−
1
0~2^4 - 1
0~24−1,则模=
2
4
(
16
)
2^4(16)
24(16)。将4位整型数能表示的所有数字画在一个圆中,从原点(0)开始,为了得到数字-5,我们可以选择沿逆时针方向移动5个位置,即
−
5
-5
−5;或者沿顺时针方向移动11个位置,即
+
11
+11
+11。在这里
5
+
11
=
16
5+11=16
5+11=16,它们互为补数,-5和+11计算得到了相同的结果。那么在这个模数系统中,理论上实现了负数到正数的转换,即负数可以通过0加上该数的补数得到。
相关参考
- 《深入理解计算机系统》
- 《计算机组成与体系结构性能设计》


