Keras（一）Sequential模型及实践

本文介绍tf.Keras中最常用的模型结构Sequential模型，并分享一个Sequential模型实例

Sequential 模型

Sequential模型是Keras中最常用的模型，是一个线性、顺序的模型。
特点是模型的每一层都拥有一个唯一的输入tensor和输出tensor。

构建一个Sequential模型有以下两种写法：

# Define Sequential model with 3 layers
model = keras.Sequential(
    [
        layers.Dense(2, activation="relu", name="layer1"),
        layers.Dense(3, activation="relu", name="layer2"),
        layers.Dense(4, name="layer3"),
    ]
)
# Call model on a test input
x = tf.ones((3, 3))
y = model(x)

# Create 3 layers
layer1 = layers.Dense(2, activation="relu", name="layer1")
layer2 = layers.Dense(3, activation="relu", name="layer2")
layer3 = layers.Dense(4, name="layer3")

# Call layers on a test input
x = tf.ones((3, 3))
y = layer3(layer2(layer1(x)))

Dense

tf.keras.layers.Dense创建一个全连接层，以下是参数：

tf.keras.layers.Dense(
    units,                                 # 正整数，输出空间的维数
    activation=None,                       # 激活函数，不指定则没有
    use_bias=True,							 # 布尔值，是否使用偏移向量
    kernel_initializer='glorot_uniform',   # 核权重矩阵的初始值设定项
    bias_initializer='zeros',              # 偏差向量的初始值设定项
    kernel_regularizer=None,               # 正则化函数应用于核权矩阵
    bias_regularizer=None,                 # 应用于偏差向量的正则化函数
    activity_regularizer=None,             # Regularizer function applied to the output of the layer (its "activation")
    kernel_constraint=None,                # Constraint function applied to the kernel weights matrix.
    bias_constraint=None, **kwargs         # Constraint function applied to the bias vector
)

全连接层在整个网络卷积神经网络中起到“特征提取器”的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的特征表示映射到样本的标记空间的作用。

卷积网络在形式上有一点点像咱们正在召开的“人民代表大会”。卷积核的个数相当于候选人，图像中不同的特征会激活不同的“候选人”（卷积核）。池化层（仅指最大池化）起着类似于“合票”的作用，不同特征在对不同的“候选人”有着各自的喜好。
全连接相当于是“代表普选”。所有被各个区域选出的代表，对最终结果进行“投票”，全连接保证了receiptive field 是整个图像，既图像中各个部分（所谓所有代表），都有对最终结果影响的权利。

实例

本文介绍一个用Sequential CNN做图像分类的实例，数据来源于: https://github.com/zalandoresearch/fashion-mnist
分类图像中的衣物。

本文所提供的数据集是csv格式的，包含测试集和数据集，打印出head():

文件读入和预处理（将2维reshape成3维）：

# import files
data_train_file = "./Datasets/fashion-mnist_train.csv"
data_test_file = "./Datasets/fashion-mnist_test.csv"

# read files csv
df_train = pd.read_csv(data_train_file)
df_test = pd.read_csv(data_test_file)

# data as array in order to reshape them
train_data = np.array(df_train, dtype='float32')
test_data = np.array(df_test, dtype='float32')

# Normalize pixel values
X_train = train_data[:,1:]/255.0
y_train = train_data[:,0]
X_test = test_data[:,1:]/255.0
y_test = test_data[:,0]

print("X_train shape", X_train.shape)
print("y_train shape", y_train.shape)
print("X_test shape", X_test.shape)
print("y_test shape", y_test.shape)

# reshape
X_train_reshaped = X_train.reshape(X_train.shape[0],*(28,28,1))
X_test_reshaped = X_test.reshape(X_test.shape[0],*(28,28,1))
print(f'x_test shape: {X_train_reshaped.shape}')

X_train shape (60000, 784)
y_train shape (60000,)
X_test shape (10000, 784)
y_test shape (10000,)
x_test shape: (60000, 28, 28, 1)

预览一下转换后的图片

import matplotlib.pyplot as plt

plt.figure(figsize = (10,10))

for i in range(30):
    plt.subplot(6,6,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(X_train_reshaped[i])
    plt.xlabel(y_train[i])
plt.show()

模型：

model = keras.Sequential([
    layers.Conv2D(32,(3,3), activation = 'relu', input_shape = (28,28,1)),
    layers.MaxPooling2D((2,2)),
    layers.Conv2D(64,(3,3), activation = 'relu'),
    layers.MaxPooling2D((2,2)),
    layers.Conv2D(64,(3,3), activation = 'relu'),
    layers.Flatten(),
    layers.Dense(64, activation = 'relu'),
    layers.Dense(10)
], name='Seq1')

model.summary()

plot模型

tf.keras.utils.plot_model(model, show_shapes=True)

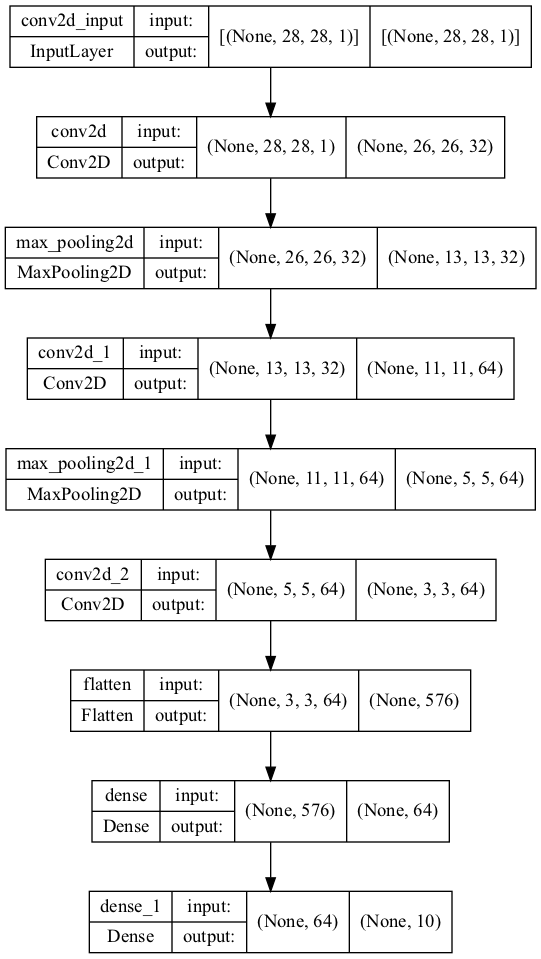
保存模型

model.save('Sequential-01')

构建和训练

model.compile(optimizer = 'adam', loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True), metrics = ['accuracy'])
history = model.fit(X_train_reshaped, y_train, epochs=10, validation_data=(X_test_reshaped, y_test))

打印准确率

import seaborn as sns

acc = {'accuracy': history.history['accuracy'],
      'val accuracy': history.history['val_accuracy']}

sns.lineplot(data=acc)

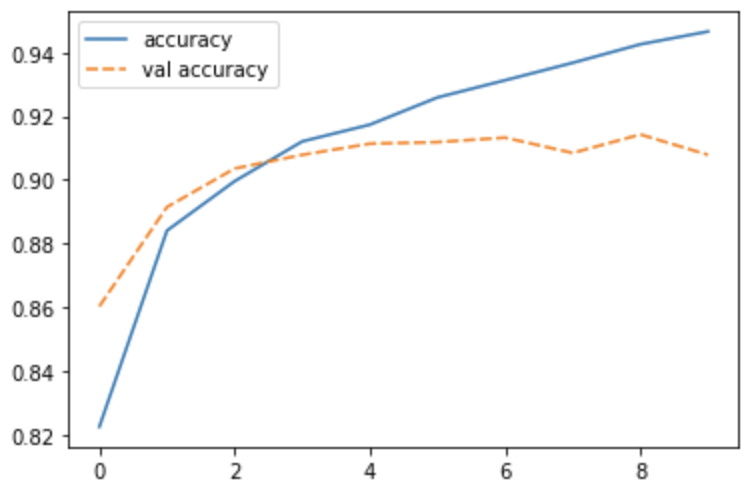
介绍下本模型用到的，也是CNN中常见的概念

Conv2D

tf.keras.layers.Conv2D是keras中2D的卷积层，一般用于图像。

Flatten

将输入扁平化，将n维的tensor投影到1维，也是模型从高维的数据变行到输出的标签的常用工具。

池化

池化（Pooling）是卷积神经网络中另一个重要的概念，它实际上是一种形式的降采样。
Keras中提供平均池化（AveragePool）和最大池化（MaxPool）
最大池化将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。
平均池化则输出其平均值。
池化的作用：减小输出大小 和 降低过拟合。降低过拟合是减小输出大小的结果，它同样也减少了后续层中的参数的数量。