Quadtree（四叉树）& Octree（八叉树）
四叉树（Quadtree）或四元树也被称为Q树（Q-Tree）。四叉树广泛应用于图像处理、空间数据索引、2D中的快速碰撞检测、存储稀疏数据等，而八叉树（Octree）主要应用于3D图形处理。对游戏编程，激光雷达点云处理等会很有用。
四叉树和八叉树实际上是二叉树在二维和三维的引申。
四叉树
四叉树的定义是：它的每个节点下至多可以有四个子节点，通常把一部分二维空间细分为四个象限或区域并把该区域里的相关信息存入到四叉树节点中。这个区域可以是正方形、矩形或是任意形状。
四叉树的每一个节点代表一个矩形区域（如上图黑色的根节点代表最外围黑色边框的矩形区域），每一个矩形区域又可划分为四个小矩形区域，这四个小矩形区域作为四个子节点所代表的矩形区域。
插入
插入函数用于将节点插入到现有的四叉树中。该函数首先检查给定节点是否在当前四边形的边界内。如果不是，则立即停止插入。如果它在边界内，我们根据其位置选择适当的子节点来包含该节点。
时间复杂度O(Log N)其中N是距离的大小。
查询
搜索函数用于定位给定四边形中的一个节点。还可以修改它以返回离给定点最近的节点。这个函数是通过取给定的点，与子四边形的边界进行比较并递归实现的。
时间复杂度是O(Log N) N是距离的大小。
代码
1 // C++ Implementation of Quad Tree 2 #include <iostream> 3 #include <cmath> 4 using namespace std; 5 6 // Used to hold details of a point 7 struct Point 8 { 9 int x; 10 int y; 11 Point(int _x, int _y) 12 { 13 x = _x; 14 y = _y; 15 } 16 Point() 17 { 18 x = 0; 19 y = 0; 20 } 21 }; 22 23 // The objects that we want stored in the quadtree 24 struct Node 25 { 26 Point pos; 27 int data; 28 Node(Point _pos, int _data) 29 { 30 pos = _pos; 31 data = _data; 32 } 33 Node() 34 { 35 data = 0; 36 } 37 }; 38 39 // The main quadtree class 40 class Quad 41 { 42 // Hold details of the boundary of this node 43 Point topLeft; 44 Point botRight; 45 46 // Contains details of node 47 Node *n; 48 49 // Children of this tree 50 Quad *topLeftTree; 51 Quad *topRightTree; 52 Quad *botLeftTree; 53 Quad *botRightTree; 54 55 public: 56 Quad() 57 { 58 topLeft = Point(0, 0); 59 botRight = Point(0, 0); 60 n = NULL; 61 topLeftTree = NULL; 62 topRightTree = NULL; 63 botLeftTree = NULL; 64 botRightTree = NULL; 65 } 66 Quad(Point topL, Point botR) 67 { 68 n = NULL; 69 topLeftTree = NULL; 70 topRightTree = NULL; 71 botLeftTree = NULL; 72 botRightTree = NULL; 73 topLeft = topL; 74 botRight = botR; 75 } 76 void insert(Node*); 77 Node* search(Point); 78 bool inBoundary(Point); 79 }; 80 81 // Insert a node into the quadtree 82 void Quad::insert(Node *node) 83 { 84 if (node == NULL) 85 return; 86 87 // Current quad cannot contain it 88 if (!inBoundary(node->pos)) 89 return; 90 91 // We are at a quad of unit area 92 // We cannot subdivide this quad further 93 if (abs(topLeft.x - botRight.x) <= 1 && 94 abs(topLeft.y - botRight.y) <= 1) 95 { 96 if (n == NULL) 97 n = node; 98 return; 99 } 100 101 if ((topLeft.x + botRight.x) / 2 >= node->pos.x) 102 { 103 // Indicates topLeftTree 104 if ((topLeft.y + botRight.y) / 2 >= node->pos.y) 105 { 106 if (topLeftTree == NULL) 107 topLeftTree = new Quad( 108 Point(topLeft.x, topLeft.y), 109 Point((topLeft.x + botRight.x) / 2, 110 (topLeft.y + botRight.y) / 2)); 111 topLeftTree->insert(node); 112 } 113 114 // Indicates botLeftTree 115 else 116 { 117 if (botLeftTree == NULL) 118 botLeftTree = new Quad( 119 Point(topLeft.x, 120 (topLeft.y + botRight.y) / 2), 121 Point((topLeft.x + botRight.x) / 2, 122 botRight.y)); 123 botLeftTree->insert(node); 124 } 125 } 126 else 127 { 128 // Indicates topRightTree 129 if ((topLeft.y + botRight.y) / 2 >= node->pos.y) 130 { 131 if (topRightTree == NULL) 132 topRightTree = new Quad( 133 Point((topLeft.x + botRight.x) / 2, 134 topLeft.y), 135 Point(botRight.x, 136 (topLeft.y + botRight.y) / 2)); 137 topRightTree->insert(node); 138 } 139 140 // Indicates botRightTree 141 else 142 { 143 if (botRightTree == NULL) 144 botRightTree = new Quad( 145 Point((topLeft.x + botRight.x) / 2, 146 (topLeft.y + botRight.y) / 2), 147 Point(botRight.x, botRight.y)); 148 botRightTree->insert(node); 149 } 150 } 151 } 152 153 // Find a node in a quadtree 154 Node* Quad::search(Point p) 155 { 156 // Current quad cannot contain it 157 if (!inBoundary(p)) 158 return NULL; 159 160 // We are at a quad of unit length 161 // We cannot subdivide this quad further 162 if (n != NULL) 163 return n; 164 165 if ((topLeft.x + botRight.x) / 2 >= p.x) 166 { 167 // Indicates topLeftTree 168 if ((topLeft.y + botRight.y) / 2 >= p.y) 169 { 170 if (topLeftTree == NULL) 171 return NULL; 172 return topLeftTree->search(p); 173 } 174 175 // Indicates botLeftTree 176 else 177 { 178 if (botLeftTree == NULL) 179 return NULL; 180 return botLeftTree->search(p); 181 } 182 } 183 else 184 { 185 // Indicates topRightTree 186 if ((topLeft.y + botRight.y) / 2 >= p.y) 187 { 188 if (topRightTree == NULL) 189 return NULL; 190 return topRightTree->search(p); 191 } 192 193 // Indicates botRightTree 194 else 195 { 196 if (botRightTree == NULL) 197 return NULL; 198 return botRightTree->search(p); 199 } 200 } 201 }; 202 203 // Check if current quadtree contains the point 204 bool Quad::inBoundary(Point p) 205 { 206 return (p.x >= topLeft.x && 207 p.x <= botRight.x && 208 p.y >= topLeft.y && 209 p.y <= botRight.y); 210 } 211 212 // Driver program 213 int main() 214 { 215 Quad center(Point(0, 0), Point(8, 8)); 216 Node a(Point(1, 1), 1); 217 Node b(Point(2, 5), 2); 218 Node c(Point(7, 6), 3); 219 center.insert(&a); 220 center.insert(&b); 221 center.insert(&c); 222 cout << "Node a: " << 223 center.search(Point(1, 1))->data << "\n"; 224 cout << "Node b: " << 225 center.search(Point(2, 5))->data << "\n"; 226 cout << "Node c: " << 227 center.search(Point(7, 6))->data << "\n"; 228 cout << "Non-existing node: " 229 << center.search(Point(5, 5)); 230 return 0; 231 }
八叉树
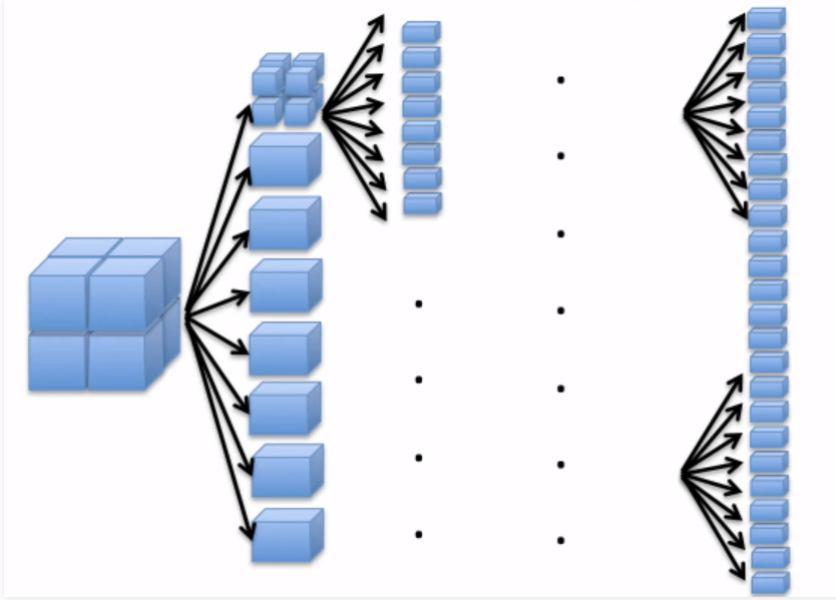
八叉树是一种树状数据结构，其中每个内部节点最多可以有8个子节点。就像二叉树把空间分成两个部分一样，八叉树把空间最多分成8个部分，用于存储空间大的三维点。如果八叉树的所有内部节点恰好包含8个子节点，则称为全八叉树。
插入
- 要在八叉树中插入一个节点，首先，我们检查一个节点是否存在，如果一个节点存在，然后返回，否则我们递归
- 首先，我们从根节点开始，并将其标记为当前节点
- 然后找到可以存储该点的子节点
- 如果节点为空，则将其替换为我们想要插入的节点，并使其成为叶节点
- 如果该节点是叶节点，则将其设置为内部节点，如果它是内部节点，则转到子节点。递归地执行这个过程，直到没有找到空节点
- 时间复杂度是O(log(N))其中N是节点数
查询
- 从根节点开始，如果找到给定点的节点，递归搜索，然后返回true，如果遇到空节点或边界点或空点，然后返回false
- 如果找到一个内部节点，就去那个节点。
- 这个函数的时间复杂度也是O(Log N)其中N是节点数
代码
1 // Implementation of Octree in c++ 2 #include <iostream> 3 #include <vector> 4 using namespace std; 5 6 #define TopLeftFront 0 7 #define TopRightFront 1 8 #define BottomRightFront 2 9 #define BottomLeftFront 3 10 #define TopLeftBottom 4 11 #define TopRightBottom 5 12 #define BottomRightBack 6 13 #define BottomLeftBack 7 14 15 // Structure of a point 16 struct Point { 17 int x; 18 int y; 19 int z; 20 Point() 21 : x(-1), y(-1), z(-1) 22 { 23 } 24 25 Point(int a, int b, int c) 26 : x(a), y(b), z(c) 27 { 28 } 29 }; 30 31 // Octree class 32 class Octree { 33 34 // if point == NULL, node is internal node. 35 // if point == (-1, -1, -1), node is empty. 36 Point* point; 37 38 // Represent the boundary of the cube 39 Point *topLeftFront, *bottomRightBack; 40 vector<Octree*> children; 41 42 public: 43 // Constructor 44 Octree() 45 { 46 // To declare empty node 47 point = new Point(); 48 } 49 50 // Constructor with three arguments 51 Octree(int x, int y, int z) 52 { 53 // To declare point node 54 point = new Point(x, y, z); 55 } 56 57 // Constructor with six arguments 58 Octree(int x1, int y1, int z1, int x2, int y2, int z2) 59 { 60 // This use to construct Octree 61 // with boundaries defined 62 if (x2 < x1 63 || y2 < y1 64 || z2 < z1) { 65 cout << "bounday poitns are not valid" << endl; 66 return; 67 } 68 69 point = nullptr; 70 topLeftFront 71 = new Point(x1, y1, z1); 72 bottomRightBack 73 = new Point(x2, y2, z2); 74 75 // Assigning null to the children 76 children.assign(8, nullptr); 77 for (int i = TopLeftFront; 78 i <= BottomLeftBack; 79 ++i) 80 children[i] = new Octree(); 81 } 82 83 // Function to insert a point in the octree 84 void insert(int x, 85 int y, 86 int z) 87 { 88 89 // If the point already exists in the octree 90 if (find(x, y, z)) { 91 cout << "Point already exist in the tree" << endl; 92 return; 93 } 94 95 // If the point is out of bounds 96 if (x < topLeftFront->x 97 || x > bottomRightBack->x 98 || y < topLeftFront->y 99 || y > bottomRightBack->y 100 || z < topLeftFront->z 101 || z > bottomRightBack->z) { 102 cout << "Point is out of bound" << endl; 103 return; 104 } 105 106 // Binary search to insert the point 107 int midx = (topLeftFront->x 108 + bottomRightBack->x) 109 / 2; 110 int midy = (topLeftFront->y 111 + bottomRightBack->y) 112 / 2; 113 int midz = (topLeftFront->z 114 + bottomRightBack->z) 115 / 2; 116 117 int pos = -1; 118 119 // Checking the octant of 120 // the point 121 if (x <= midx) { 122 if (y <= midy) { 123 if (z <= midz) 124 pos = TopLeftFront; 125 else 126 pos = TopLeftBottom; 127 } 128 else { 129 if (z <= midz) 130 pos = BottomLeftFront; 131 else 132 pos = BottomLeftBack; 133 } 134 } 135 else { 136 if (y <= midy) { 137 if (z <= midz) 138 pos = TopRightFront; 139 else 140 pos = TopRightBottom; 141 } 142 else { 143 if (z <= midz) 144 pos = BottomRightFront; 145 else 146 pos = BottomRightBack; 147 } 148 } 149 150 // If an internal node is encountered 151 if (children[pos]->point == nullptr) { 152 children[pos]->insert(x, y, z); 153 return; 154 } 155 156 // If an empty node is encountered 157 else if (children[pos]->point->x == -1) { 158 delete children[pos]; 159 children[pos] = new Octree(x, y, z); 160 return; 161 } 162 else { 163 int x_ = children[pos]->point->x, 164 y_ = children[pos]->point->y, 165 z_ = children[pos]->point->z; 166 delete children[pos]; 167 children[pos] = nullptr; 168 if (pos == TopLeftFront) { 169 children[pos] = new Octree(topLeftFront->x, 170 topLeftFront->y, 171 topLeftFront->z, 172 midx, 173 midy, 174 midz); 175 } 176 177 else if (pos == TopRightFront) { 178 children[pos] = new Octree(midx + 1, 179 topLeftFront->y, 180 topLeftFront->z, 181 bottomRightBack->x, 182 midy, 183 midz); 184 } 185 else if (pos == BottomRightFront) { 186 children[pos] = new Octree(midx + 1, 187 midy + 1, 188 topLeftFront->z, 189 bottomRightBack->x, 190 bottomRightBack->y, 191 midz); 192 } 193 else if (pos == BottomLeftFront) { 194 children[pos] = new Octree(topLeftFront->x, 195 midy + 1, 196 topLeftFront->z, 197 midx, 198 bottomRightBack->y, 199 midz); 200 } 201 else if (pos == TopLeftBottom) { 202 children[pos] = new Octree(topLeftFront->x, 203 topLeftFront->y, 204 midz + 1, 205 midx, 206 midy, 207 bottomRightBack->z); 208 } 209 else if (pos == TopRightBottom) { 210 children[pos] = new Octree(midx + 1, 211 topLeftFront->y, 212 midz + 1, 213 bottomRightBack->x, 214 midy, 215 bottomRightBack->z); 216 } 217 else if (pos == BottomRightBack) { 218 children[pos] = new Octree(midx + 1, 219 midy + 1, 220 midz + 1, 221 bottomRightBack->x, 222 bottomRightBack->y, 223 bottomRightBack->z); 224 } 225 else if (pos == BottomLeftBack) { 226 children[pos] = new Octree(topLeftFront->x, 227 midy + 1, 228 midz + 1, 229 midx, 230 bottomRightBack->y, 231 bottomRightBack->z); 232 } 233 children[pos]->insert(x_, y_, z_); 234 children[pos]->insert(x, y, z); 235 } 236 } 237 238 // Function that returns true if the point 239 // (x, y, z) exists in the octree 240 bool find(int x, int y, int z) 241 { 242 // If point is out of bound 243 if (x < topLeftFront->x 244 || x > bottomRightBack->x 245 || y < topLeftFront->y 246 || y > bottomRightBack->y 247 || z < topLeftFront->z 248 || z > bottomRightBack->z) 249 return 0; 250 251 // Otherwise perform binary search 252 // for each ordinate 253 int midx = (topLeftFront->x 254 + bottomRightBack->x) 255 / 2; 256 int midy = (topLeftFront->y 257 + bottomRightBack->y) 258 / 2; 259 int midz = (topLeftFront->z 260 + bottomRightBack->z) 261 / 2; 262 263 int pos = -1; 264 265 // Deciding the position 266 // where to move 267 if (x <= midx) { 268 if (y <= midy) { 269 if (z <= midz) 270 pos = TopLeftFront; 271 else 272 pos = TopLeftBottom; 273 } 274 else { 275 if (z <= midz) 276 pos = BottomLeftFront; 277 else 278 pos = BottomLeftBack; 279 } 280 } 281 else { 282 if (y <= midy) { 283 if (z <= midz) 284 pos = TopRightFront; 285 else 286 pos = TopRightBottom; 287 } 288 else { 289 if (z <= midz) 290 pos = BottomRightFront; 291 else 292 pos = BottomRightBack; 293 } 294 } 295 296 // If an internal node is encountered 297 if (children[pos]->point == nullptr) { 298 return children[pos]->find(x, y, z); 299 } 300 301 // If an empty node is encountered 302 else if (children[pos]->point->x == -1) { 303 return 0; 304 } 305 else { 306 307 // If node is found with 308 // the given value 309 if (x == children[pos]->point->x 310 && y == children[pos]->point->y 311 && z == children[pos]->point->z) 312 return 1; 313 } 314 return 0; 315 } 316 }; 317 318 // Driver code 319 int main() 320 { 321 Octree tree(1, 1, 1, 5, 5, 5); 322 323 tree.insert(1, 2, 3); 324 tree.insert(1, 2, 3); 325 tree.insert(6, 5, 5); 326 327 cout << (tree.find(1, 2, 3) 328 ? "Found\n" 329 : "Not Found\n"); 330 331 cout << (tree.find(3, 4, 4) 332 ? "Found\n" 333 : "Not Found\n"); 334 tree.insert(3, 4, 4); 335 336 cout << (tree.find(3, 4, 4) 337 ? "Found\n" 338 : "Not Found\n"); 339 340 return 0; 341 }
