【2017多校训练08 1002】【HDOJ 6134】Battlestation Operational

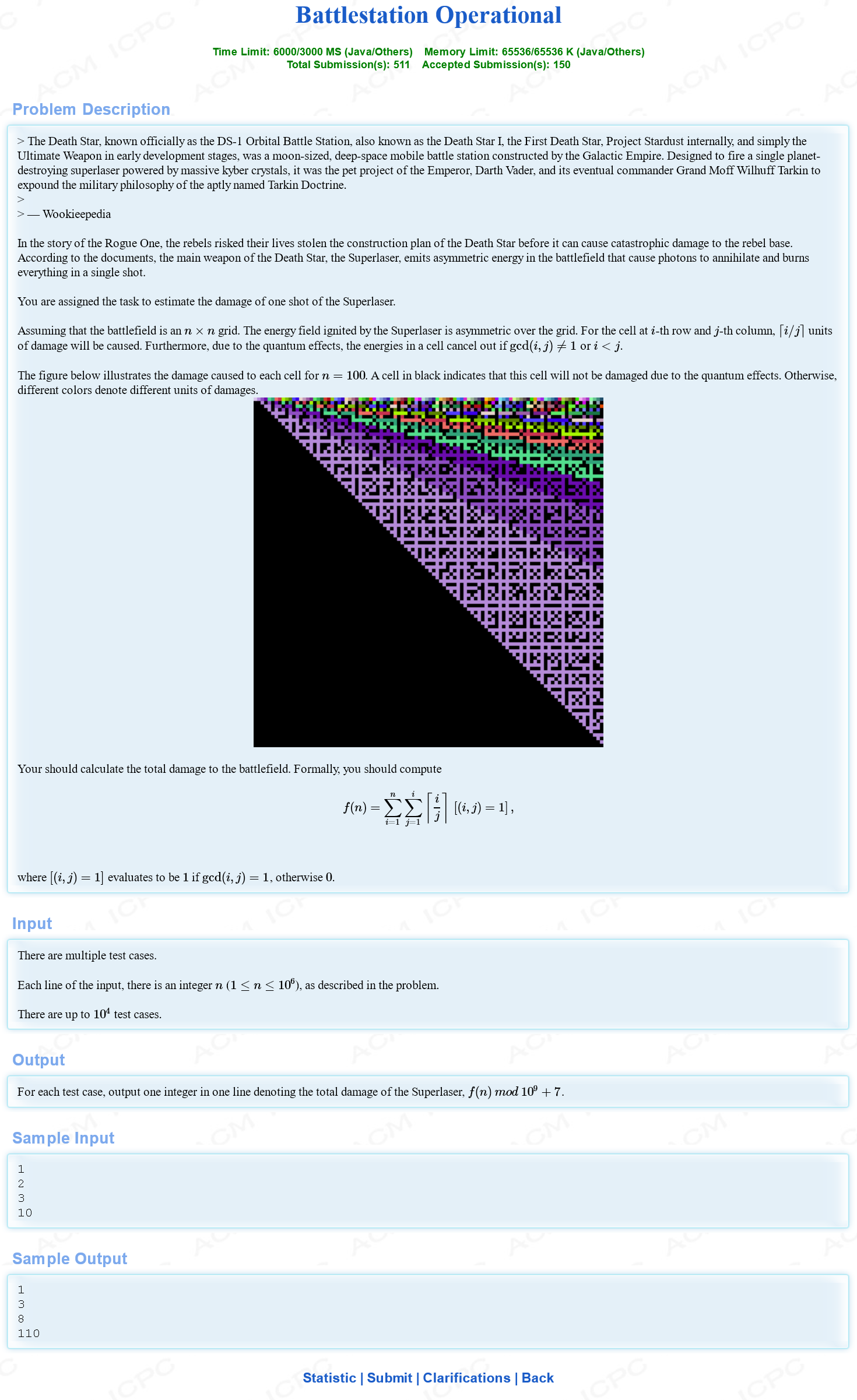
典型的数列反演题。

运用莫比乌斯反演的一个结论 $[n = 1] = \sum_{d | n} \mu(d)$，将表达式做如下转化：

$$ ans = \sum_{i=1}^n \sum_{j=1}^i (\lfloor \frac{i-1}{j} \rfloor + 1) \sum_{d | i \land d | j} \mu(d) \\ = \sum_{d=1}^n \mu(d) \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^i (\lfloor \frac{i-1}{j} \rfloor + 1) $$

令$$F_n = \sum_{i=1}^n \sum_{j=1}^i (\lfloor \frac{i-1}{j} \rfloor + 1)$$

则有$$ans = \sum_{d=1}^n \mu(d) F(\lfloor \frac{n}{d} \rfloor)$$

先考虑如何计算Fn.

观察得知，内层求和与n无直接关联，不妨直接对F相邻两项做差：

$$dF_n = F_n - F_{n-1} \\= \sum_{j=1}^n (\lfloor \frac{n-1}{j} \rfloor + 1) $$

考虑每个j对每个n的贡献。

对于一个给定的j，我们可以枚举$\lfloor \frac{n-1}{j} \rfloor$的取值t，此时j和t将对$[j*t+1, j*(t+1)+1)$这一范围内所有的n对应的$F_n$产生t+1的贡献。

由调和级数可知，对所有j枚举它们在N以内的倍数只需要O(Nlog(N))级别的时间复杂度。我们只要在枚举j和t的同时维护一下$dF_n$的相邻两项差，最后做两次前缀和就可以得到$F_n$数列了。

再来考虑如何由$F_n$计算$ans_n$。

由$ans_n = \sum_{d=1}^n \mu(d) F(\lfloor \frac{n}{d} \rfloor)$，与上一步类似，同样可以考虑每个d对每个n的答案的贡献。对于每个d，枚举$\lfloor \frac{n}{d} \rfloor$的取值t，此时d和t对$[t*d, (t+1)*d)$范围内所有的n对应的$ans_n$产生$\mu(d) * F_t$ 的贡献。枚举结束后再做一遍前缀和即可。

#include <iostream>
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 1000005, mod = 1000000007;
typedef long long LL;
int mu[maxn], muS[maxn], F[maxn], ans[maxn], P[maxn], pcnt, N;
bool not_p[maxn];

void sieve()
{
    mu[1] = 1;
    for(int i = 2;i < maxn;++i)
    {
        if(!not_p[i]) P[pcnt++] = i, mu[i] = -1;
        for(int j = 0;j < pcnt;++j)
        {
            if(i * P[j] >= maxn) break;
            not_p[i * P[j]] = true;
            if(i % P[j] == 0)
            {
                mu[i * P[j]] = 0;
                break;
            }
            else mu[i * P[j]] = -mu[i];
        }
    }
}

void init()
{
    sieve();
    for(int i = 2;i <= N;++i) muS[i] = muS[i-1] + mu[i];
    N = 1000000;
    int L, R;
    for(int k = 1;k < N;++k)
    {
        L = k, R = k+k;
        for(int t = 1;L < N;++t, L += k, R += k)
        {
            F[L+1] = (F[L+1] + t) % mod;
            if(R < N) F[R+1] = (F[R+1] - t) % mod;
            //if(L < 3) printf("k = %d, (%d, %d] = %d\n", k, L, N, t);
        }
    }
    for(int i = 2;i <= N;++i) F[i] = (F[i] + F[i-1]) % mod;
    for(int i = 2;i <= N;++i) F[i] = (F[i] + F[i-1]) % mod;
    for(int i = 1;i <= N;++i)
        F[i] = (F[i] + (LL) i * (i+1) / 2) % mod;
    for(int i = 1;i <= N;++i) //F[d]
    {
        for(int j = 1, k = i;k <= N;++j, k += i)
        {
            int tmp = (mod + F[j] * mu[i]) % mod;
            ans[k] = (ans[k] + tmp) % mod;
            if(k+i <= N) ans[k+i] = (ans[k+i] + mod - tmp) % mod;
        }
    }
    for(int i = 2;i <= N;++i) ans[i] = (ans[i] + ans[i-1]) % mod;
}

void work()
{
    while(~scanf("%d", &N))
    {
        printf("%d\n", ans[N]);
    }
}
int main() {
    // your code goes here
    int T;
    init();
    work();
    return 0;
}