通过坐标点和距离来检索指定范围点的相关笔记

需求描述

检索某个坐标点附近200米的门店, 使用矩形匹配上下边界的方式来加快数据库检索

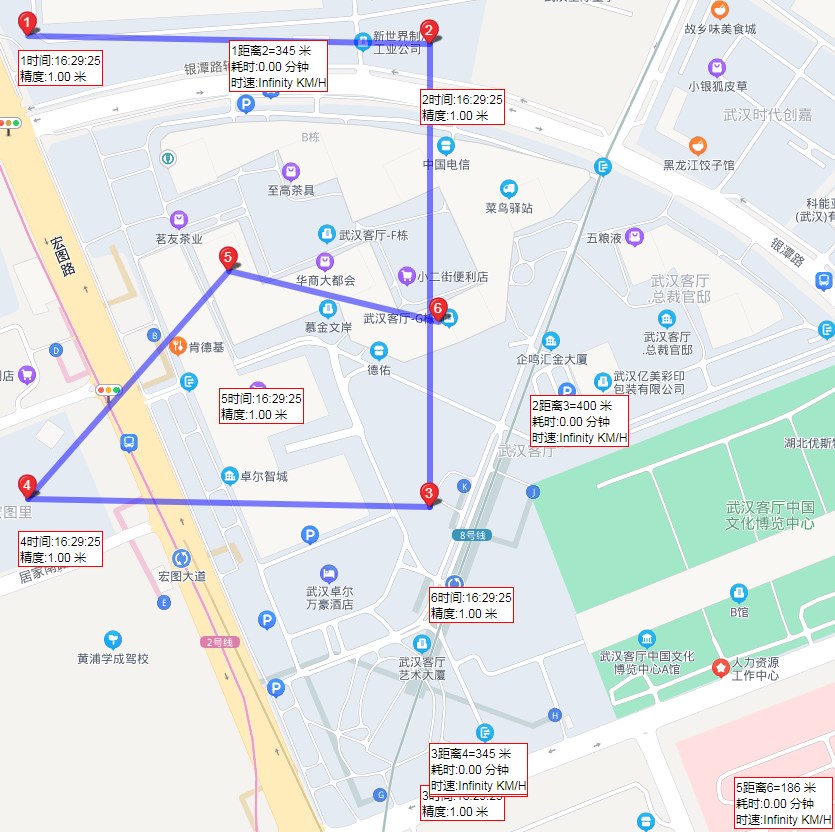
错误的算法X出问题的示意图

实际需求: 检索序号5的点附近200米的点6

解决方案: 为了提升查询数据库的检索性能,采用的是通过序号5的点上下左右加200米的方式来取出尽可能多的点.用多取点,来换取性能

碰到问题: 算法X无法正常检索到点6 (点5和点6的距离只有186米), 按理论算法,200的圆应该包含在算出的矩形内才对.

问题示意图:

1-4 = 用序号5的点+200米用算法X得到的矩形4个角的位置
横向1到2的距离居然是345米(不是400米!), 纵向2到3的距离是正常的400米.

最终方案:修复原来的较低精度,算法简单的原始版本算法X

var lat = Deg2rad(pPoint.Latitude);
var lon = Deg2rad(pPoint.Longitude);

var radius = GetEarthRadius(lat);
var pradius = radius * Math.Cos(lat);

var latMin = lat - pDistance / radius;
var latMax = lat + pDistance / radius;
//var lonMin = lon - pDistance / radius/*修复前*/;
//var lonMax = lon + pDistance / radius/*修复前*/;
var lonMin = lon - pDistance / pradius/*修复后*/;
var lonMax = lon + pDistance / pradius/*修复后*/;

pMinPoint = new Coordinate() { Latitude =Rad2deg(latMin), Longitude =Rad2deg(lonMin) };
pMaxPoint = new Coordinate() { Latitude=Rad2deg(latMax),Longitude= Rad2deg(lonMax) };

吐槽:一顿操作猛如虎,结果都是复制粘贴惹的BUG

//1.较低精度,算法简单的版本
Coordinate minPoint1;
Coordinate maxPoint1;
LBSUtil.GetBoundingBox(point1, 200, out minPoint1, out maxPoint1);

//2.最高精度,算法复杂的版本
var one = new GlobalCoordinates(point1.Latitude, point1.Longitude);
var x = 282.842712474619;//算出200直角三角形对应的斜边长度=282
var calc = new GeodeticCalculator(Ellipsoid.WGS84);
var rt = calc.CalculateEndingGlobalCoordinates(one, 45, x);
var rb = calc.CalculateEndingGlobalCoordinates(one, 90 + 45, x);
var lb = calc.CalculateEndingGlobalCoordinates(one, 180 + 45, x);
var lt = calc.CalculateEndingGlobalCoordinates(one, 270 + 45, x);
double maxLng = 0, minLng = 9999, maxLat = 0, minLat = 9999;
foreach (var i in new[] {rt, rb, lb, lt})
{
    maxLng = Math.Max(maxLng, i.Longitude.Degrees);
    minLng = Math.Min(minLng, i.Longitude.Degrees);
    maxLat = Math.Max(maxLat, i.Latitude.Degrees);
    minLat = Math.Min(minLat, i.Latitude.Degrees);
}

有效的解决方案:使用最精准的算法vincenty,算法最复杂

https://github.com/chrisveness/geodesy

目的是拥有清晰，简单的说明性代码示例，这些示例可以在其他项目中进行调整和重用（无论是用JavaScript，Java，C++，Excel VBA还是其他任何东西进行编码）。
凭借其非类型化的C风格语法，JavaScript的读取非常接近伪代码，以最小的语法干扰公开算法。
具有历史基准面转换（例如在 NAD83、OSGB36、Irl1975 等之间）和现代参考坐标系转换（如 ITRF2014、ETRF2000、GDA94 等）以及大地测量（纬度/经度）坐标和地心笛卡尔（x/y/z）坐标之间的转换的功能
球面接地模型提供了简单的公式，涵盖了大多数“日常”精度要求;椭圆体-地球模型以牺牲复杂性为代价提供了更精确的公式。
基于向量的函数为基于trig的函数提供了另一种方法，具有一些重叠的功能;使用哪一个可能取决于相关功能的可用性或其他考虑因素。
https://github.com/chrisveness/geodesy/blob/master/latlon-ellipsoidal-vincenty.js

椭圆体上测地线的 Vincenty 直解和逆解（c） Chris Veness 2002-2022 麻省理工学院执照
之间的距离和方位角，以及给定起点和初始方位的目的地点在椭圆体地球模型上使用测地线的“测地线的直解和逆解”在椭球体由Thaddeus Vincenty设计。

Usage in browser

import LatLon from 'https://cdn.jsdelivr.net/npm/geodesy@2.4.0/latlon-ellipsoidal-vincenty.js
new LatLon(-37.95103, 144.42487).destinationPoint(dist, brng)

NuGet 库|大地测量学 4.1.0 https://www.nuget.org/packages/Geodesy/

这是一个 C# 类库，其中包含一些非常基本的测地线算法。它基于Mike Gavaghan的作品
（见 http://www.gavaghan.org/blog/free-source-code/geodesy-library-vincentys-formula/)
并且由我增强，以涵盖墨卡托投影地球到平面地图的一些变体。
我将介绍球面和椭圆墨卡托投影，将地球映射到单个平面地图。
我还处理通用横轴墨卡托（UTM）投影，将地球划分为更小的网格，然后将每个网格映射到平面地图。
最后 - 基于UTM - 我实现了一种算法，在地球的映射区域上放置更细的粒度网格，以便能够按离散的全球唯一网格数对地理位置进行分类。
只要复制以下几个文件到项目中即可实现大部分功能

Angle.cs
Ellipsoid.cs
ExtendDouble.cs
GeodeticCalculator.cs
GeodeticCurve.cs
GeodeticMeasurement.cs
GlobalCoordinates.cs
GlobalPosition.cs

var one = new GlobalCoordinates(point1.Latitude, point1.Longitude);
var x = 282.842712474619;//算出200直角三角形对应的斜边长度=282
var calc = new GeodeticCalculator(Ellipsoid.WGS84);
var rt = calc.CalculateEndingGlobalCoordinates(one, 45, x);
var rb = calc.CalculateEndingGlobalCoordinates(one, 90 + 45, x);
var lb = calc.CalculateEndingGlobalCoordinates(one, 180 + 45, x);
var lt = calc.CalculateEndingGlobalCoordinates(one, 270 + 45, x);
double maxLng = 0, minLng = 9999, maxLat = 0, minLat = 9999;
foreach (var i in new[] {rt, rb, lb, lt})
{
    maxLng = Math.Max(maxLng, i.Longitude.Degrees);
    minLng = Math.Min(minLng, i.Longitude.Degrees);
    maxLat = Math.Max(maxLat, i.Latitude.Degrees);
    minLat = Math.Min(minLat, i.Latitude.Degrees);
}
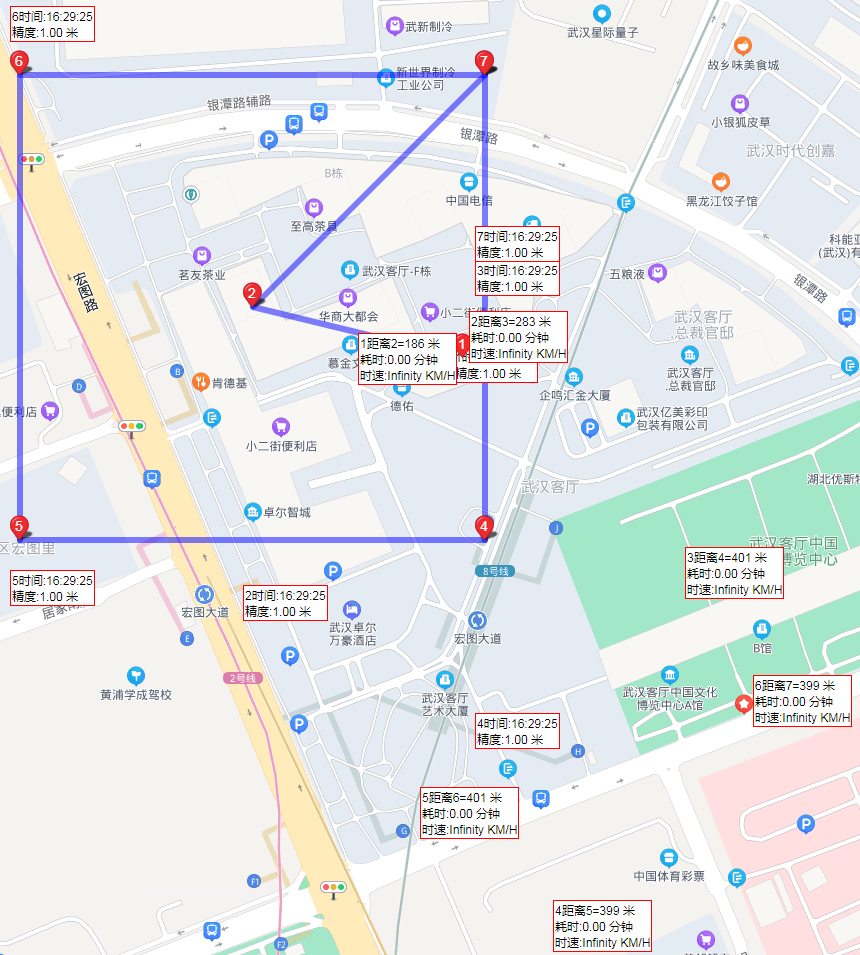
//即可得到右上角,左下角的2个点,足够构成一个边长400的正方形.

1=有问题的门店点

2=用户当前定位的点

3-7=最大矩形,必须能内切一个半径为200圆的矩形.

斜边=282.842712474619

3-045:114.28710249537777,30.679541589539700
4-135:114.28710241779460,30.675933563422774
5-225:114.28292817239038,30.675933563422774
6-315:114.28292809480725,30.679541589539706

MAX=114.28710249537777,30.679541589539706
MIN=114.28292809480725,30.675933563422774
有了MAX和MIN就可以通过数据库比对查询结果了.

核对看看取了最大最小之后的矩形和原矩形是否偏差过大,
实际测试结果肉眼观察是几乎没有偏差ByYe.

<script type="module">
import LatLon from 'https://cdn.jsdelivr.net/npm/geodesy@2.4.0/latlon-ellipsoidal-vincenty.js';
const findHypotenuse = (base, perpendicular) => {
   const bSquare = base ** 2;
   const pSquare = perpendicular ** 2;
   const sum = bSquare + pSquare;
   const hypotenuse = Math.sqrt(sum);
   return hypotenuse;
};
var items = [];

//有问题的门店所在点
var result = gcoord.transform([114.280364,30.671525], // 经纬度坐标
                              gcoord.GCJ02, // 当前坐标系
                              gcoord.BD09// 目标坐标系
                             );
items.push({
                LAT: result[1],
                LNG: result[0],
                Accuracy: 1
            });

//当前定位到的点
var result = gcoord.transform([114.278487,30.671888], // 经纬度坐标
                              gcoord.GCJ02, // 当前坐标系
                              gcoord.BD09// 目标坐标系
                             );
var one;
items.push(one={
                LAT: result[1],
                LNG: result[0],
                Accuracy: 1
            });


const p1 = new LatLon(one.LAT, one.LNG);
const dist = findHypotenuse(200,200);//计算目标范围200米对应的斜边长度,用来画一个包含内切一个200半径的圆的正方形矩形.
let brng = 45;
let p2 = p1.destinationPoint(dist, brng);
            items.push({
                LAT: p2.lat,
                LNG: p2.lng,
                Accuracy: 1
            });
 brng = 90+45;
 p2 = p1.destinationPoint(dist, brng);
            items.push({
                LAT: p2.lat,
                LNG: p2.lng,
                Accuracy: 1
            });
 brng = 180+45;
 p2 = p1.destinationPoint(dist, brng);
            items.push({
                LAT: p2.lat,
                LNG: p2.lng,
                Accuracy: 1
            });
 brng = 270+45;
 p2 = p1.destinationPoint(dist, brng);
            items.push({
                CollectDateTime: '2022-06-27 16:29:25',
                LAT: p2.lat,
                LNG: p2.lng,
                Accuracy: 1
            });
 brng = 360+45;
 p2 = p1.destinationPoint(dist, brng);
            items.push({
                LAT: p2.lat,
                LNG: p2.lng,
                Accuracy: 1
            });

//核对看看取了最大最小之后的矩形和原矩形是否偏差过大,实际测试结果肉眼观察是几乎没有偏差ByYe.
// MAX=114.28710249537777,30.679541589539706
// MIN=114.28292809480725,30.675933563422774
addNumberMarker(new BMap.Point(114.28710249537777,30.679541589539706), 9);
addNumberMarker(new BMap.Point(114.28710249537777,30.675933563422774), 9);
addNumberMarker(new BMap.Point(114.28292809480725,30.679541589539706), 9);
addNumberMarker(new BMap.Point(114.28292809480725,30.675933563422774), 9);

参考资料

JavaScript 中椭圆体上测地线的 Vincenty 解|可移动类型脚本 http://www.movable-type.co.uk/scripts/latlong-vincenty.html

Vincenty对椭圆体地球模型上点间距离的解在所使用的椭圆体上精确到0.5毫米距离（！），0.000015“方位角内。
基于球形地球模型的计算，例如（更简单的）Haversine，精确到0.3%左右
注意：Vincenty的解决方案是使用球形模型提高精度的好方法。但是，如果您正在寻找比一米左右更好的精度，则可能需要更深入地了解一些细节。
无处不在的WGS-84被定义为精确到不超过±1米左右;有关更多详细信息，请参阅下文。
JavaScript（略微简化，忽略收敛，赤道线，重合/对跖情况等）
目的地给定距离和起点的方位（直接解决方案）
请参阅下面的 JavaScript 源代码，也可以在 https://github.com/chrisveness/geodesy 上找到。提供完整的文档以及测试套件。

GitHub - geocoder-php/Geocoder：用 PHP 编写的最具特色的 Geocoder 库。 https://github.com/geocoder-php/Geocoder

Geocoder 是一个 PHP 库，它通过为地理编码操作提供强大的抽象层来帮助您构建地理感知应用程序。
提供程序为您执行地理编码黑魔法（与 API 通信、获取结果、处理错误等），并且高度可配置。
cache-provider 包装提供程序并缓存结果
chain-provider 循环访问多个提供程序
google-maps-provider 地址，反向
bing-maps-provider 地址，反向
host-ip-provider IPv4

https://github.com/thephpleague/geotools/

Geotools is a PHP geo-related library, built atop Geocoder and React libraries.
支持 23 种不同的椭球体
在通用横轴墨卡托（UTM）投影中转换十进制度坐标
使用平坦、大圆、哈弗正弦或文森特算法计算两个坐标之间的距离（默认为米）、公里、英里或英尺。
计算目标点（坐标），给定方位单位为度，距离（以米为单位）
多边形类提供了检查 poing（坐标）是否在多边形边界内或多边形边界上的方法。
默认大地基准面为 WGS84，坐标以十进制度为单位。
它提供了使用平坦（最高性能），大圆，哈弗正弦或文森特（最准确）算法计算两个坐标之间的距离（默认情况下），km，mi或ft的方法。这些坐标应位于同一椭球体中。
using flat (most performant), great circle, haversine or vincenty (most accurate) algorithms.
geotools/Distance.php at c4d43e95f21c97ba97ebe87c3a7f63684da0f9d4 · thephpleague/geotools · GitHub https://github.com/thephpleague/geotools/blob/c4d43e95f21c97ba97ebe87c3a7f63684da0f9d4/src/Distance/Distance.php

使用 Vincenty 逆返回两个坐标之间的大地测量距离精确到 0.5mm 以内的椭圆体公式。‎
http://www.movable-type.co.uk/scripts/latlong-vincenty.html

正向计算器 https://www.ngs.noaa.gov/cgi-bin/Inv_Fwd/forward2.prl

使用前方位角和椭圆体距离计算新的大地测量位置
纬度和经度的默认半球设置在“北”和“西”。
椭圆体 GRS80 （NAD83） / WGS84

Adding Distance To GPS Coordinates To Get Bounding Box - PHP - SitePoint Forums | Web Development & Design Community
https://www.sitepoint.com/community/t/adding-distance-to-gps-coordinates-to-get-bounding-box/5820/10

寻找一种方法来添加到起始GPS坐标点的距离，以创建一个边界框（近似一个圆），然后我将使用它来查找该框中MySQL数据库中的所有匹配项。
考虑地球的曲率，即表面上的距离
radius = 3963.1; // of earth in miles 因此，脚本必须不准确。
如果有任何数学和PHP大师可以采用Haversine公式并将其修改为返回点坐标而不是距离，请告诉我。
// Radius of earth. 3959 miles or 6371 kilometers千米公里. Must set radius to units you are using, in my case, miles.
计算两个GPS坐标之间的距离（PHP - Haversine公式）
一个sql查询，你给它一个纬度/lng设置一个半径，它从数据库中选择所有纬度/lng

查找离您地址最近的位置 - PHP - SitePoint 论坛|网站开发与设计社区 https://www.sitepoint.com/community/t/find-the-closest-location-near-your-address/3297
曲率=6371.04

FizzyCalc
http://www.fizzymagic.net/Geocaching/FizzyCalc/index.html

允许将坐标简单转换为各种格式
使用Vincenty方法进行高精度距离计算和投影，以计算椭球体上的距离
与大多数GPS设备相同的方式进行基准面转换。可在 100 多个不同基准之间进行转换。

PHP 库：计算给定纬度/液化天然气位置的边界框 - fsou
https://stackoverflow.nilmap.com/question?dest_url=https://stackoverflow.com/questions/2628039/php-library-calculate-a-bounding-box-for-a-given-lat-lng-location

使用椭圆体公式（例如WGS84）会很棒

正确的距离计算算法

以下正确的算法都能正常算出横向距离1到2为345; 纵向距离2到3为400;

百度地图的

百度地图JSAPI 2.0类参考

https://lbsyun.baidu.com/cms/jsapi/reference/jsapi_reference.html

new Map().getDistance(start: Point, end: Point)	//Number	返回两点之间的距离，单位是米

Android官方的

android.location.Location.java

计算两个地点之间的近似距离（米），以及可选择的初始和最终方位。它们之间的最短路径。距离和方位的定义是使用WGS84椭球体。

计算出的距离被存储在results[0]中。如果结果有长度2或更大，初始方位就存储在results[1]中。如果结果有长度为3或更大，最终的方位被存储在results[2]中。

基于 http://www.ngs.noaa.gov/PUBS_LIB/inverse.pdf

使用 "逆向公式"（第4节）。
Bessel 6377397.155
lnternational 6378388.000
参考资料里有提到Vincenty算法

    public float distanceTo(@NonNull final LocationEx location)
    {
        float[] results = new float[1];
        Location.distanceBetween(location.getLatitude(), location.getLongitude(), getLatitude(), getLongitude(), results);
        return results[0];
    }

项目中有问题的算法X

const double WGS84_A = 6378137.0;    //Major semiaxis [m]
const double WGS84_B = 6356752.3;    //Minor semiaxis [m]

/// <summary>
/// 以指定的点为中心,以距离为半径,获取一个矩形范围
/// </summary>
/// <param name="pPoint">中心点</param>
/// <param name="pDistance">距离（单位：米）</param>
public static void GetBoundingBox(Coordinate pPoint,double pDistance,out Coordinate pMinPoint,out Coordinate pMaxPoint)
{
    var lat = Deg2rad(pPoint.Latitude);
    var lon = Deg2rad(pPoint.Longitude);

    var radius = GetEarthRadius(lat);
    var pradius = radius * Math.Cos(lat);

    var latMin = lat - pDistance / radius;
    var latMax = lat + pDistance / radius;
    var lonMin = lon - pDistance / radius;
    var lonMax = lon + pDistance / radius;

    pMinPoint = new Coordinate() { Latitude =Rad2deg(latMin), Longitude =Rad2deg(lonMin) };
    pMaxPoint = new Coordinate() { Latitude=Rad2deg(latMax),Longitude= Rad2deg(lonMax) };
}

private static double Deg2rad(double pDegree)
{
    return Math.PI * pDegree / 180.0;
}
private static double Rad2deg(double pRadians)
{
    return 180.0 * pRadians / Math.PI;
}

private static double GetEarthRadius(double pLat)
{
    var an = WGS84_A * WGS84_A * Math.Cos(pLat);
    var bn = WGS84_B * WGS84_B * Math.Sin(pLat);
    var ad = WGS84_A * Math.Cos(pLat);
    var bd = WGS84_B * Math.Sin(pLat);
    return Math.Sqrt((an * an + bn * bn) / (ad * ad + bd * bd));
}

使用百度地图测试点的位置相关代码

<!DOCTYPE html>
<html>
    <head>
        <script type="text/javascript" src="http://api.map.baidu.com/api?v=2.0&ak="></script>
        <script src="https://unpkg.com/gcoord/dist/gcoord.js"></script>
    </head>
    <body>
        <div id="allmap"></div>
    </body>
</html>
<script type="module">
import LatLon from 'https://cdn.jsdelivr.net/npm/geodesy@2.4.0/latlon-ellipsoidal-vincenty.js';

var map = new BMap.Map("allmap");
map.enableScrollWheelZoom(true);

function addMarker(point, info) //
{
    var marker = new BMap.Marker(point);
    map.addOverlay(marker);
    var label = new BMap.Label(info ? info : point.lat + ',' + point.lng,{
        offset: new BMap.Size(0,-120 + (Math.random() * 500))
    });
    marker.setLabel(label);
}

const base = 200;
const perpendicular = 200;
const findHypotenuse = (base, perpendicular) => {
   const bSquare = base ** 2;
   const pSquare = perpendicular ** 2;
   const sum = bSquare + pSquare;
   const hypotenuse = Math.sqrt(sum);
   return hypotenuse;
};
    console.log(findHypotenuse(200,200));

var result = gcoord.transform([114.278487,30.671888], // 经纬度坐标
                              gcoord.GCJ02, // 当前坐标系
                              gcoord.BD09// 目标坐标系
                             );

items.push(one={
    CollectDateTime: '2022-06-27 16:29:25',
    LAT: result[1],
    LNG: result[0],
    Accuracy: 1
});
    console.log('center one lat:'+one.LAT+',lng:'+one.LNG);
const p1 = new LatLon(one.LAT, one.LNG);
const dist = findHypotenuse(200,200);
let brng = 45;
let p2 = p1.destinationPoint(dist, brng);
items.push({
    LAT: p2.lat,
    LNG: p2.lng
});
console.log(brng+':'+p2.lng+','+p2.lat);

// MAX=114.28710249537777,30.679541589539706
// MIN=114.28292809480725,30.675933563422774
// addNumberMarker(new BMap.Point(114.28710249537777,30.679541589539706), 9);
// addNumberMarker(new BMap.Point(114.28710249537777,30.675933563422774), 9);
// addNumberMarker(new BMap.Point(114.28292809480725,30.679541589539706), 9);
// addNumberMarker(new BMap.Point(114.28292809480725,30.675933563422774), 9);

// maxPoint1 = Coordinate
//  Latitude = {double} 30.679535783764134
//  Longitude = {double} 114.28710609104209
// addNumberMarker(new BMap.Point(114.28710609104209,30.679535783764134), 9);
// addNumberMarker(new BMap.Point(114.28710609104209,30.675939403228814), 8);

//  minPoint1 = Coordinate
//  Latitude = {double} 30.675939403228814
//  Longitude = {double} 114.28292449914291
// addNumberMarker(new BMap.Point(114.28292449914291,30.679535783764134), 7);
// addNumberMarker(new BMap.Point(114.28292449914291,30.675939403228814), 6);


// maxLat = {double} 30.679541589539724
// maxLng = {double} 114.28710249537778
addNumberMarker(new BMap.Point(114.28710249537778,30.679541589539724), 9);
addNumberMarker(new BMap.Point(114.28710249537778,30.675933563422774), 8);
    
// minLat = {double} 30.675933563422774
// minLng = {double} 114.28292809480718
addNumberMarker(new BMap.Point(114.28292809480718,30.679541589539724), 7);
addNumberMarker(new BMap.Point(114.28292809480718,30.675933563422774), 6);
</script>

posted @ 2022-06-28 16:50 Asion Tang 阅读(384) 评论(0) 编辑收藏举报

刷新页面返回顶部