最小生成树 (Minimum Spanning Tree,MST) --- Prim算法

本文链接:http://www.cnblogs.com/Ash-ly/p/5409904.html

普瑞姆(Prim)算法:

　　假设N = (V, {E})是连通网，TE是N上最小生成树边的集合,U是是顶点集V的一个非空子集，算法从U = {uo}(u0 属于 V)，TE = {}开始，重复执行下述动作:

　　在所有u属于U，v属于V - U的边(u, v)，且(u, v)属于E中找一条代价最小的边(u0, v0)并并入集合TE中，同时v0并入U,直至U = V为止。此时TE中必有n - 1条边，则T = (V, {TE})为N的最小生成树。

　　为了实现这个算法，需要另设一个辅助数组lowcost，lowcost[i]代表V - U中点 i 到 U中某点的最小代价。假如用edge[x][y] 代表 x 和 y 之间的代价为edge[x][y]，那么lowcost[i] = Min{edge[i][j] | i 属于 V - U, j 属于 U}。

　　时间复杂度:O(n^2)，适合点少边多稠密图。

用图描述:

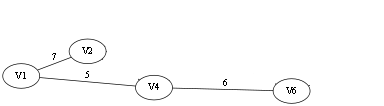
N的初始图:

假设从V1开始生成，T 为最终的MST，G 为(V - T{v}, E - T{e} - (lowcost[i], T{v}) | lowcost[i] = INF)(有点乱貌似，继续看图吧)

则图T:　　　　　　　　　　　　　　　　　　　　　　则图G:　　　　　　　　　　

lowcost[i]代表N 中的每个点能连通T的最小代价，点 i 如果不能直接和 T 中某点连通则值应为INF(无穷大)，如果点 i 已经属于T，则标记为红色，值为-1。

可以看到 N 中的 V4 到T的代价最短，则选择 V4 加入 T 中。

则图T变为:　　　　　　　　　　　　　　　　　　　　　则图G变为:

由于V4的加入，所以需要更新lowcost数组，lowcost[i] = min(lowcost[i], edge[i][v4])(i 属于 V(G))。lowcost[v2] = 7，而edge[v2][v4] = 9,那么lowcost[v2] 仍然是 7;locost[v3] = INF，而edge[v3][v4] = INF，那么lowcost[v3] 仍然是 INF;lowcost[v4][v4] = -1;lowcost[v5] = INF，而edge[v5][v4] = 15，那么应该把lowcost[v5]更新为15;同理edge[v6][v4] < lowcost[v6]，则应该更新为 6;lowcost[v7]不变。

则lowcost变为:

可以看到，lowcost[v6]代价最小,那么选择V6加入T中

则图T变为:　　　　　　　　　　　　　　　　　　　　　则图G变为:

继续根据更新lowcost的公式,lowcost[i] = min(lowcost[i], edge[v6][i]),(i 属于 V(G))更新lowcost数组。

则lowcost变为:

继续选择代价最小的，lowcost[v2] 最小，那么把 v2 加入 T 中

则图T变为:　　　　　　　　　　　　　　　　　　　　　则图G变为:

执行lowcost[i] = min(lowcost[i], edge[v2][i])。

则得到的lowcost数组为：

同样选择代价最小的lowcost[v5]，即把V5加入T中。

则图T变为:　　　　　　　　　　　　　　　　　　　　　则图G变为:

执行lowcost[i] = min(lowcost[i], edge[v5][i])。

则得到的lowcost数组为：

继续选择代价最小的lowcost[V3]，把V3加入到T中

则图T变为:　　　　　　　　　　　　　　　　　　　　　则图G变为:

执行lowcost[i] = min(lowcost[i], edge[v3][i])。

则得到的lowcost数组为：

显而易见，选择V7加入T中

则图T变为:　

至此，算法结束，得到的图T就是所寻找的MST！！！

代码( 未优化, 时间复杂度: O(N²) ):

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <algorithm>
using namespace std;

const int MAXN = 103;
const int INF = 0x3f3f3f3f;    //最大值
int edge[MAXN][MAXN];        //邻接矩阵
int used[MAXN];         //标记这个点是否在最小生成树的集合(是否在T中)里面  0 代表未加入  1 代表加入
int lowcost[MAXN];      //存放的是未被加入集合的点(G中的点)到已经被加入集合的点(T中的点)的最短距离
int N,M;

int prim(int start,int maxn)    //假设 从 start 开始寻找MST， maxn  代表点的个数
{
   used[start] = 1;
   for(int i = 1; i <= maxn; i++)    //刚开始只有start 这个点在集合里面 所以初始化这个数组为到集合之外的各个点的距离 ，如果没有则是无穷大（INF）
   {
       lowcost[i] = edge[start][i];
   }
   int sumweight = 0;    // MST 的权值
   int ok = 0;
   for(int i = 1; i <= maxn; i++)
   {
       int minn = INF ;   //为找到最短的那条边
       int v = -1;          //标记找的那个点
       for(int j = 1; j <= maxn; j++)     //开始寻找集合之外得点到集合之里的点的最短边
       {
           if(used[j] == 0 && lowcost[j] < minn)   //在集合之外的点寻找最短的边
           {
               minn = lowcost[j];
               v = j;  
           }
       }
       if(v != -1)    //找到了 v  这个点
       {
           ok++;
           used[v] = 1;   //标记已被使用
           sumweight += lowcost[v];   //更新权值
           for(int j = 1; j <= maxn; j++)      //更新存放最短边的集合(lowcost)
           {
               if(used[j] == 0 && lowcost[j] > edge[v][j])    //在集合之外(G)得点 寻找到集合之里(T)各个点的最短边 更新数组
               {
                   lowcost[j] = edge[v][j];
               }
           }
       }
   }
   if(ok == maxn -1)    //找到了
     return sumweight;
   return -1;     //没找到
}

int main()
{
    while(cin >> N >> M && N)
    {
        memset(edge, 0x3f, sizeof(edge));  //清空为最大值
        memset(used, 0, sizeof(used));    //刚开始所有的点都在集合之外
        while(N--)
        {
            int u, v, w;
            cin >> u >> v >> w;
            edge[u][v] = edge[v][u] = w;
        }
        int ans = prim(1, M);       //从 1 这个点开始找 一共有M个点
        if(ans < 0) cout << "?" <<endl;
        else cout << ans << endl;
    }
    return 0;
}

堆优化:假设 Vb 为MST的点集合, Va为不属于MST的点集和, Vb初始化仅有起点 s, Va 为其余所有点, 上面算法是用一个数组 lowcost 来维护 Va 中的点到 Vb 中的点的最短距离,但是每次更新时需要遍历所有点集,这是一步很耗时的操作,在这里可以用堆来对其进行优化.使用堆(Binary Heap)来保存 Va 中每一点到 Vb 中所有点的最短边长并维护其最小值,并在访问每条边的时候更新.由于堆比较复杂,STL油提供了现成的堆(priority_queue)

代码( 优先队列(堆) + Prim, 时间复杂度O( (N + M) * logN ) ):

 1 const int MAXN = 10000; 
 2 const int MAXE = 100000;
 3 const int INF = 0x3f3f3f3f;
 4 int n, m;
 5 bool visit[MAXN + 3];
 6 int lowcost[MAXN + 3];
 7 int pre[MAXN + 3];
 8 
 9 int head[MAXN + 3], len;
10 struct EDGE { int to; int next; int w; };
11 EDGE edge[2 * MAXE + 3];
12 
13 void addedge(int u, int v, int w) { 
14     edge[len].to = v;
15     edge[len].w = w;
16     edge[len].next = head[u];
17     head[u] = len++;
18 }
19 
20 struct NODE { //队列中的节点
21     int v; int w; //点  v 到 MST 集合中的距离为 w
22     NODE () {}
23     NODE (int u, int wh) {v = u, w = wh;}
24     bool operator < (const NODE& a) const {
25         if(w == a.w) return v > a.v;
26         return w > a.w;
27     }
28     NODE& operator = (const NODE & a) {
29         v = a.v, w = a.w;
30         return *this;
31     }
32 };
33 
34 int prim(int st) {
35     memset(visit, false, sizeof(visit));
36     memset(pre, -1, sizeof(pre));
37     for(int i = 0; i <= n; i++) lowcost[i] = INF;
38     lowcost[st] = 0, pre[st] = st;
39     priority_queue<NODE> minhp;
40     minhp.push( NODE(st, 0) );    //初始节点入队
41     int mst = 0, cnt = 0;
42     while( !minhp.empty() ) {
43         NODE tp = minhp.top(); minhp.pop(); //从队列首部取出最近的节点, 并删除
44         if(visit[tp.v]) continue;
45         visit[tp.v] = true; //标记已访问节点
46         mst += tp.w, cnt++;//记录MST权值以及MST集合中的点的个数
47         for(int k = head[tp.v], j; k != -1; k = edge[k].next) {
48             if(!visit[j = edge[k].to] && edge[k].w < lowcost[j]) {//更新最短边长度
49                 pre[j] = tp.v;
50                 lowcost[j] = edge[k].w;
51                 minhp.push( NODE(j, lowcost[j]) );
52             }
53         }
54     }
55     return cnt == n ?  mst : -1;
56 }

posted @ 2016-04-19 20:12 vrsashly 阅读(1042) 评论(0) 编辑收藏举报

刷新页面返回顶部

vrsashly

It's not numeral, punctuation and character. It's my life!

最小生成树 (Minimum Spanning Tree,MST) --- Prim算法