算法复习——虚树(消耗战bzoj2286)
题目:
Description
在一场战争中,战场由n个岛屿和n-1个桥梁组成,保证每两个岛屿间有且仅有一条路径可达。现在,我军已经侦查到敌军的总部在编号为1的岛屿,而且他们已经没有足够多的能源维系战斗,我军胜利在望。已知在其他k个岛屿上有丰富能源,为了防止敌军获取能源,我军的任务是炸毁一些桥梁,使得敌军不能到达任何能源丰富的岛屿。由于不同桥梁的材质和结构不同,所以炸毁不同的桥梁有不同的代价,我军希望在满足目标的同时使得总代价最小。
侦查部门还发现,敌军有一台神秘机器。即使我军切断所有能源之后,他们也可以用那台机器。机器产生的效果不仅仅会修复所有我军炸毁的桥梁,而且会重新随机资源分布(但可以保证的是,资源不会分布到1号岛屿上)。不过侦查部门还发现了这台机器只能够使用m次,所以我们只需要把每次任务完成即可。
Input
第一行一个整数n,代表岛屿数量。
接下来n-1行,每行三个整数u,v,w,代表u号岛屿和v号岛屿由一条代价为c的桥梁直接相连,保证1<=u,v<=n且1<=c<=100000。
第n+1行,一个整数m,代表敌方机器能使用的次数。
接下来m行,每行一个整数ki,代表第i次后,有ki个岛屿资源丰富,接下来k个整数h1,h2,…hk,表示资源丰富岛屿的编号。
Output
输出有m行,分别代表每次任务的最小代价。
Sample Input
10
1 5 13
1 9 6
2 1 19
2 4 8
2 3 91
5 6 8
7 5 4
7 8 31
10 7 9
3
2 10 6
4 5 7 8 3
3 9 4 6
1 5 13
1 9 6
2 1 19
2 4 8
2 3 91
5 6 8
7 5 4
7 8 31
10 7 9
3
2 10 6
4 5 7 8 3
3 9 4 6
Sample Output
12
32
22
32
22
HINT
对于100%的数据,2<=n<=250000,m>=1,sigma(ki)<=500000,1<=ki<=n-1
Source
题解:
先发泄一下:
bzoj输出量大了不能用cout!!!!!!!
bzoj输出量大了不能用cout!!!!!!!
bzoj输出量大了不能用cout!!!!!!!
艹艹艹艹艹艹卡了我一个下午!!!!!
接下说下关于虚树的知识:




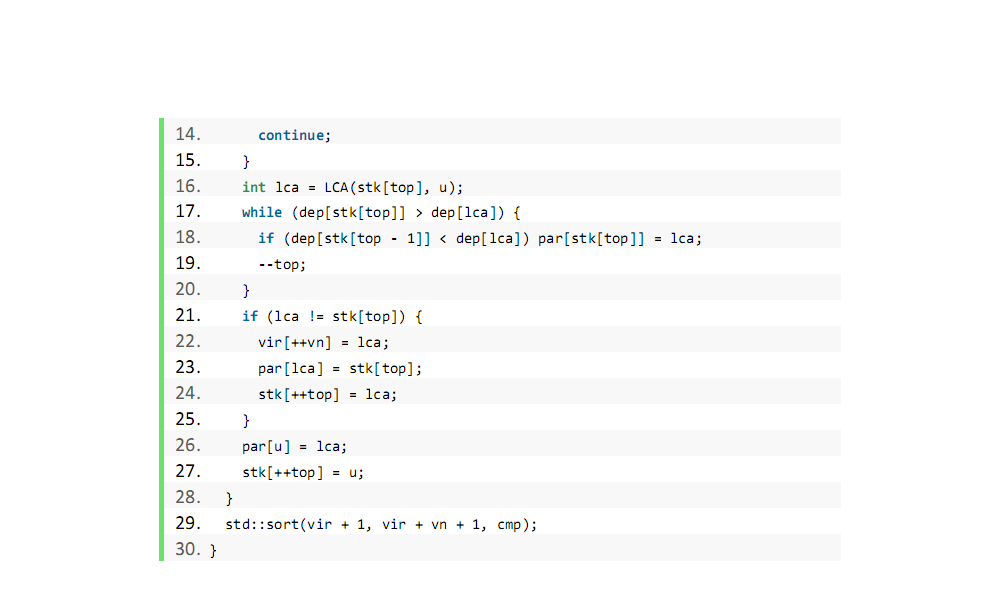
然后这道题就是虚树+简单的树形dp即可,注意在新建虚树边的时候不要直接memset,否则会超时····
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<string> #include<cstring> #include<algorithm> using namespace std; const int N=250005; int dfn[N],first[N],go[N*2],nxt[N*2],tot=0,n,m,g[N][26],deep[N],cnt=0,vn,tn,tem; int tot1=0,first1[N],go1[N*2],next1[N*2],par[N],tag[N]; int vir[N],stack[N],top=0; long long dp[N],val[N*2],minn[N]; inline void comb(int a,int b,long long c) { nxt[++tot]=first[a],first[a]=tot,go[tot]=b,val[tot]=c; nxt[++tot]=first[b],first[b]=tot,go[tot]=a,val[tot]=c; } inline void comb1(int a,int b) { next1[++tot1]=first1[a],first1[a]=tot1,go1[tot1]=b; } inline int R() { char c; int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } inline long long Rl() { char c; long long f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=f*10+c-'0'; return f; } inline void dfs(int u,int fa) { dfn[u]=++cnt; for(int e=first[u];e;e=nxt[e]) { int v=go[e]; if(v==fa) continue; deep[v]=deep[u]+1; g[v][0]=u; minn[v]=min(minn[u],val[e]); dfs(v,u); } } inline int get(int a,int b) { int i,j; if(deep[a]<deep[b]) swap(a,b); for(i=0;(1<<i)<=deep[a];i++); i--; for(j=i;j>=0;j--) { if(deep[a]-(1<<j)>=deep[b]) a=g[a][j]; } if(a==b) return a; for(j=25;j>=0;j--) { if(g[a][j]!=g[b][j]) { a=g[a][j]; b=g[b][j]; } } return g[a][0]; } inline void pre() { tot1=0,stack[top=0]=0,tem++; } bool cmp(const int &a,const int &b) { return dfn[a]<dfn[b]; } inline void build() { sort(vir+1,vir+vn+1,cmp); vn=unique(vir+1,vir+vn+1)-vir-1; tn=vn; for(int i=1;i<=tn;i++) { int u=vir[i]; if(!top) { par[u]=0; stack[++top]=u; continue; } int lca=get(stack[top],u); while(deep[stack[top]]>deep[lca]) { if(deep[stack[top-1]]<deep[lca]) par[stack[top]]=lca; top--; } if(stack[top]!=lca) { vir[++vn]=lca; par[lca]=stack[top]; stack[++top]=lca; } par[u]=lca; stack[++top]=u; } sort(vir+1,vir+vn+1,cmp); } inline long long solve(int u) { if(tag[u]==tem) return minn[u]; dp[u]=minn[u]; long long temp=0; bool flag=false; for(int e=first1[u];e;e=next1[e]) { int v=go1[e]; flag=true; temp+=solve(v); } if(flag) dp[u]=min(dp[u],temp); return dp[u]; } int main() { //freopen("a.in","r",stdin); n=R(); int a,b; long long c; for(int i=1;i<n;i++) { a=R(),b=R(),c=Rl(); comb(a,b,c); } minn[1]=1e+18; deep[1]=1; dfs(1,0); for(int i=1;i<=25;i++) for(int j=1;j<=n;j++) g[j][i]=g[g[j][i-1]][i-1]; m=R(); for(int i=1;i<=m;i++) { pre(),vn=R(); for(int j=1;j<=vn;j++) vir[j]=R(),tag[vir[j]]=tem; build(); for(int j=1;j<=vn;j++) first1[vir[j]]=dp[vir[j]]=0; for(int j=2;j<=vn;j++) comb1(par[vir[j]],vir[j]); dp[vir[1]]=solve(vir[1]); printf("%lld\n",dp[vir[1]]); } return 0; }


